CopyQNN: Quantum Neural Network Extraction Attack under Varying Quantum Noise

Quantum Neural Networks (QNNs) have shown significant value across domains, with well-trained QNNs representing critical intellectual property often deployed via cloud-based QNN-as-a-Service (QNNaaS) platforms. Recent work has examined QNN model extraction attacks using classical and emerging quantum strategies. These attacks involve adversaries querying QNNaaS platforms to obtain labeled data for training local substitute QNNs that replicate the functionality of cloud-based models. However, existing approaches have largely overlooked the impact of varying quantum noise inherent in noisy intermediate-scale quantum (NISQ) computers, limiting their effectiveness in real-world settings. To address this limitation, we propose the CopyQNN framework, which employs a three-step data cleaning method to eliminate noisy data based on its noise sensitivity. This is followed by the integration of contrastive and transfer learning within the quantum domain, enabling efficient training of substitute QNNs using a limited but cleaned set of queried data. Experimental results on NISQ computers demonstrate that a practical implementation of CopyQNN significantly outperforms state-of-the-art QNN extraction attacks, achieving an average performance improvement of 8.73% across all tasks while reducing the number of required queries by 90x, with only a modest increase in hardware overhead.

One-step Diffusion Models with $f$-Divergence Distribution Matching

Sampling from diffusion models involves a slow iterative process that hinders their practical deployment, especially for interactive applications. To accelerate generation speed, recent approaches distill a multi-step diffusion model into a single-step student generator via variational score distillation, which matches the distribution of samples generated by the student to the teacher's distribution. However, these approaches use the reverse Kullback-Leibler (KL) divergence for distribution matching which is known to be mode seeking. In this paper, we generalize the distribution matching approach using a novel $f$-divergence minimization framework, termed $f$-distill, that covers different divergences with different trade-offs in terms of mode coverage and training variance. We derive the gradient of the $f$-divergence between the teacher and student distributions and show that it is expressed as the product of their score differences and a weighting function determined by their density ratio. This weighting function naturally emphasizes samples with higher density in the teacher distribution, when using a less mode-seeking divergence. We observe that the popular variational score distillation approach using the reverse-KL divergence is a special case within our framework. Empirically, we demonstrate that alternative $f$-divergences, such as forward-KL and Jensen-Shannon divergences, outperform the current best variational score distillation methods across image generation tasks. In particular, when using Jensen-Shannon divergence, $f$-distill achieves current state-of-the-art one-step generation performance on ImageNet64 and zero-shot text-to-image generation on MS-COCO. Project page: https://research.nvidia.com/labs/genair/f-distill

Energy-Based Diffusion Language Models for Text Generation

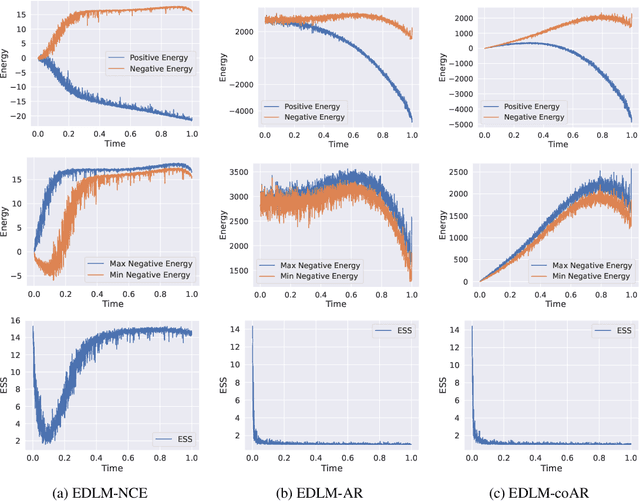
Despite remarkable progress in autoregressive language models, alternative generative paradigms beyond left-to-right generation are still being actively explored. Discrete diffusion models, with the capacity for parallel generation, have recently emerged as a promising alternative. Unfortunately, these models still underperform the autoregressive counterparts, with the performance gap increasing when reducing the number of sampling steps. Our analysis reveals that this degradation is a consequence of an imperfect approximation used by diffusion models. In this work, we propose Energy-based Diffusion Language Model (EDLM), an energy-based model operating at the full sequence level for each diffusion step, introduced to improve the underlying approximation used by diffusion models. More specifically, we introduce an EBM in a residual form, and show that its parameters can be obtained by leveraging a pretrained autoregressive model or by finetuning a bidirectional transformer via noise contrastive estimation. We also propose an efficient generation algorithm via parallel important sampling. Comprehensive experiments on language modeling benchmarks show that our model can consistently outperform state-of-the-art diffusion models by a significant margin, and approaches autoregressive models' perplexity. We further show that, without any generation performance drop, our framework offers a 1.3$\times$ sampling speedup over existing diffusion models.

Hamiltonian Score Matching and Generative Flows

Classical Hamiltonian mechanics has been widely used in machine learning in the form of Hamiltonian Monte Carlo for applications with predetermined force fields. In this work, we explore the potential of deliberately designing force fields for Hamiltonian ODEs, introducing Hamiltonian velocity predictors (HVPs) as a tool for score matching and generative models. We present two innovations constructed with HVPs: Hamiltonian Score Matching (HSM), which estimates score functions by augmenting data via Hamiltonian trajectories, and Hamiltonian Generative Flows (HGFs), a novel generative model that encompasses diffusion models and flow matching as HGFs with zero force fields. We showcase the extended design space of force fields by introducing Oscillation HGFs, a generative model inspired by harmonic oscillators. Our experiments validate our theoretical insights about HSM as a novel score matching metric and demonstrate that HGFs rival leading generative modeling techniques.

Heavy-Tailed Diffusion Models

Diffusion models achieve state-of-the-art generation quality across many applications, but their ability to capture rare or extreme events in heavy-tailed distributions remains unclear. In this work, we show that traditional diffusion and flow-matching models with standard Gaussian priors fail to capture heavy-tailed behavior. We address this by repurposing the diffusion framework for heavy-tail estimation using multivariate Student-t distributions. We develop a tailored perturbation kernel and derive the denoising posterior based on the conditional Student-t distribution for the backward process. Inspired by $\gamma$-divergence for heavy-tailed distributions, we derive a training objective for heavy-tailed denoisers. The resulting framework introduces controllable tail generation using only a single scalar hyperparameter, making it easily tunable for diverse real-world distributions. As specific instantiations of our framework, we introduce t-EDM and t-Flow, extensions of existing diffusion and flow models that employ a Student-t prior. Remarkably, our approach is readily compatible with standard Gaussian diffusion models and requires only minimal code changes. Empirically, we show that our t-EDM and t-Flow outperform standard diffusion models in heavy-tail estimation on high-resolution weather datasets in which generating rare and extreme events is crucial.

Truncated Consistency Models

Consistency models have recently been introduced to accelerate sampling from diffusion models by directly predicting the solution (i.e., data) of the probability flow ODE (PF ODE) from initial noise. However, the training of consistency models requires learning to map all intermediate points along PF ODE trajectories to their corresponding endpoints. This task is much more challenging than the ultimate objective of one-step generation, which only concerns the PF ODE's noise-to-data mapping. We empirically find that this training paradigm limits the one-step generation performance of consistency models. To address this issue, we generalize consistency training to the truncated time range, which allows the model to ignore denoising tasks at earlier time steps and focus its capacity on generation. We propose a new parameterization of the consistency function and a two-stage training procedure that prevents the truncated-time training from collapsing to a trivial solution. Experiments on CIFAR-10 and ImageNet $64\times64$ datasets show that our method achieves better one-step and two-step FIDs than the state-of-the-art consistency models such as iCT-deep, using more than 2$\times$ smaller networks. Project page: https://truncated-cm.github.io/

Think While You Generate: Discrete Diffusion with Planned Denoising

Discrete diffusion has achieved state-of-the-art performance, outperforming or approaching autoregressive models on standard benchmarks. In this work, we introduce Discrete Diffusion with Planned Denoising (DDPD), a novel framework that separates the generation process into two models: a planner and a denoiser. At inference time, the planner selects which positions to denoise next by identifying the most corrupted positions in need of denoising, including both initially corrupted and those requiring additional refinement. This plan-and-denoise approach enables more efficient reconstruction during generation by iteratively identifying and denoising corruptions in the optimal order. DDPD outperforms traditional denoiser-only mask diffusion methods, achieving superior results on language modeling benchmarks such as text8, OpenWebText, and token-based generation on ImageNet $256 \times 256$. Notably, in language modeling, DDPD significantly reduces the performance gap between diffusion-based and autoregressive methods in terms of generative perplexity. Code is available at https://github.com/liusulin/DDPD.

Neural Augmentation Based Panoramic High Dynamic Range Stitching

Due to saturated regions of inputting low dynamic range (LDR) images and large intensity changes among the LDR images caused by different exposures, it is challenging to produce an information enriched panoramic LDR image without visual artifacts for a high dynamic range (HDR) scene through stitching multiple geometrically synchronized LDR images with different exposures and pairwise overlapping fields of views (OFOVs). Fortunately, the stitching of such images is innately a perfect scenario for the fusion of a physics-driven approach and a data-driven approach due to their OFOVs. Based on this new insight, a novel neural augmentation based panoramic HDR stitching algorithm is proposed in this paper. The physics-driven approach is built up using the OFOVs. Different exposed images of each view are initially generated by using the physics-driven approach, are then refined by a data-driven approach, and are finally used to produce panoramic LDR images with different exposures. All the panoramic LDR images with different exposures are combined together via a multi-scale exposure fusion algorithm to produce the final panoramic LDR image. Experimental results demonstrate the proposed algorithm outperforms existing panoramic stitching algorithms.

DisCo-Diff: Enhancing Continuous Diffusion Models with Discrete Latents

Diffusion models (DMs) have revolutionized generative learning. They utilize a diffusion process to encode data into a simple Gaussian distribution. However, encoding a complex, potentially multimodal data distribution into a single continuous Gaussian distribution arguably represents an unnecessarily challenging learning problem. We propose Discrete-Continuous Latent Variable Diffusion Models (DisCo-Diff) to simplify this task by introducing complementary discrete latent variables. We augment DMs with learnable discrete latents, inferred with an encoder, and train DM and encoder end-to-end. DisCo-Diff does not rely on pre-trained networks, making the framework universally applicable. The discrete latents significantly simplify learning the DM's complex noise-to-data mapping by reducing the curvature of the DM's generative ODE. An additional autoregressive transformer models the distribution of the discrete latents, a simple step because DisCo-Diff requires only few discrete variables with small codebooks. We validate DisCo-Diff on toy data, several image synthesis tasks as well as molecular docking, and find that introducing discrete latents consistently improves model performance. For example, DisCo-Diff achieves state-of-the-art FID scores on class-conditioned ImageNet-64/128 datasets with ODE sampler.

Heterophilous Distribution Propagation for Graph Neural Networks

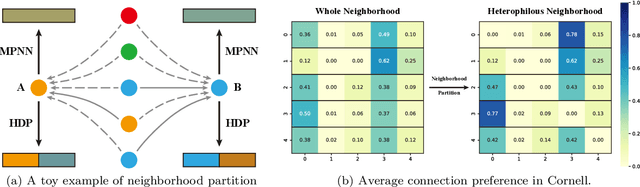
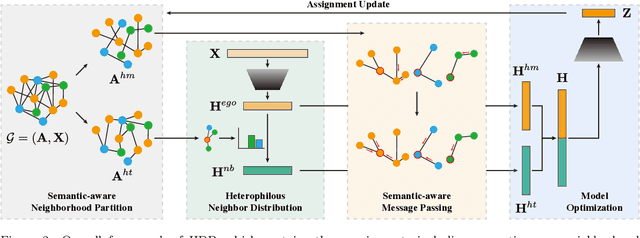
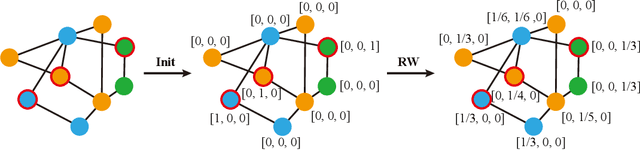
Graph Neural Networks (GNNs) have achieved remarkable success in various graph mining tasks by aggregating information from neighborhoods for representation learning. The success relies on the homophily assumption that nearby nodes exhibit similar behaviors, while it may be violated in many real-world graphs. Recently, heterophilous graph neural networks (HeterGNNs) have attracted increasing attention by modifying the neural message passing schema for heterophilous neighborhoods. However, they suffer from insufficient neighborhood partition and heterophily modeling, both of which are critical but challenging to break through. To tackle these challenges, in this paper, we propose heterophilous distribution propagation (HDP) for graph neural networks. Instead of aggregating information from all neighborhoods, HDP adaptively separates the neighbors into homophilous and heterphilous parts based on the pseudo assignments during training. The heterophilous neighborhood distribution is learned with orthogonality-oriented constraint via a trusted prototype contrastive learning paradigm. Both the homophilous and heterophilous patterns are propagated with a novel semantic-aware message passing mechanism. We conduct extensive experiments on 9 benchmark datasets with different levels of homophily. Experimental results show that our method outperforms representative baselines on heterophilous datasets.