Heterophilous Distribution Propagation for Graph Neural Networks

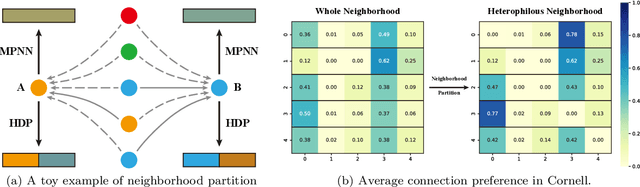
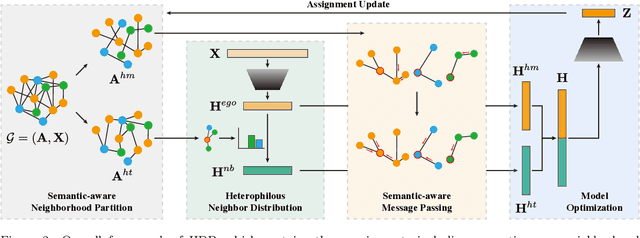
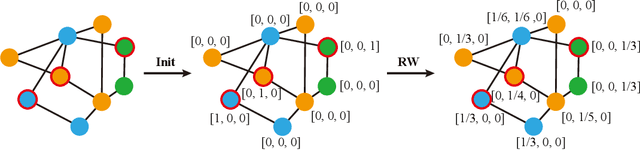
Graph Neural Networks (GNNs) have achieved remarkable success in various graph mining tasks by aggregating information from neighborhoods for representation learning. The success relies on the homophily assumption that nearby nodes exhibit similar behaviors, while it may be violated in many real-world graphs. Recently, heterophilous graph neural networks (HeterGNNs) have attracted increasing attention by modifying the neural message passing schema for heterophilous neighborhoods. However, they suffer from insufficient neighborhood partition and heterophily modeling, both of which are critical but challenging to break through. To tackle these challenges, in this paper, we propose heterophilous distribution propagation (HDP) for graph neural networks. Instead of aggregating information from all neighborhoods, HDP adaptively separates the neighbors into homophilous and heterphilous parts based on the pseudo assignments during training. The heterophilous neighborhood distribution is learned with orthogonality-oriented constraint via a trusted prototype contrastive learning paradigm. Both the homophilous and heterophilous patterns are propagated with a novel semantic-aware message passing mechanism. We conduct extensive experiments on 9 benchmark datasets with different levels of homophily. Experimental results show that our method outperforms representative baselines on heterophilous datasets.

A Survey on Graph Condensation

Analytics on large-scale graphs have posed significant challenges to computational efficiency and resource requirements. Recently, Graph condensation (GC) has emerged as a solution to address challenges arising from the escalating volume of graph data. The motivation of GC is to reduce the scale of large graphs to smaller ones while preserving essential information for downstream tasks. For a better understanding of GC and to distinguish it from other related topics, we present a formal definition of GC and establish a taxonomy that systematically categorizes existing methods into three types based on its objective, and classify the formulations to generate the condensed graphs into two categories as modifying the original graphs or synthetic completely new ones. Moreover, our survey includes a comprehensive analysis of datasets and evaluation metrics in this field. Finally, we conclude by addressing challenges and limitations, outlining future directions, and offering concise guidelines to inspire future research in this field.

Hilbert Distillation for Cross-Dimensionality Networks

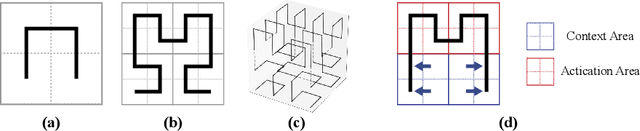
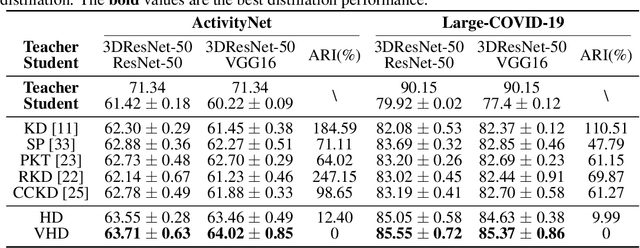
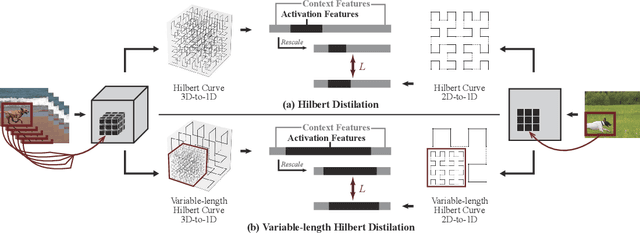
3D convolutional neural networks have revealed superior performance in processing volumetric data such as video and medical imaging. However, the competitive performance by leveraging 3D networks results in huge computational costs, which are far beyond that of 2D networks. In this paper, we propose a novel Hilbert curve-based cross-dimensionality distillation approach that facilitates the knowledge of 3D networks to improve the performance of 2D networks. The proposed Hilbert Distillation (HD) method preserves the structural information via the Hilbert curve, which maps high-dimensional (>=2) representations to one-dimensional continuous space-filling curves. Since the distilled 2D networks are supervised by the curves converted from dimensionally heterogeneous 3D features, the 2D networks are given an informative view in terms of learning structural information embedded in well-trained high-dimensional representations. We further propose a Variable-length Hilbert Distillation (VHD) method to dynamically shorten the walking stride of the Hilbert curve in activation feature areas and lengthen the stride in context feature areas, forcing the 2D networks to pay more attention to learning from activation features. The proposed algorithm outperforms the current state-of-the-art distillation techniques adapted to cross-dimensionality distillation on two classification tasks. Moreover, the distilled 2D networks by the proposed method achieve competitive performance with the original 3D networks, indicating the lightweight distilled 2D networks could potentially be the substitution of cumbersome 3D networks in the real-world scenario.

A Comprehensive Survey on Deep Clustering: Taxonomy, Challenges, and Future Directions

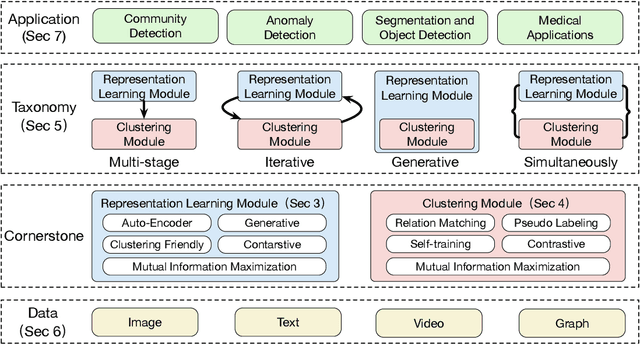
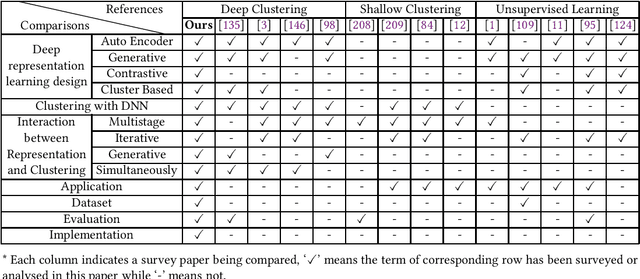
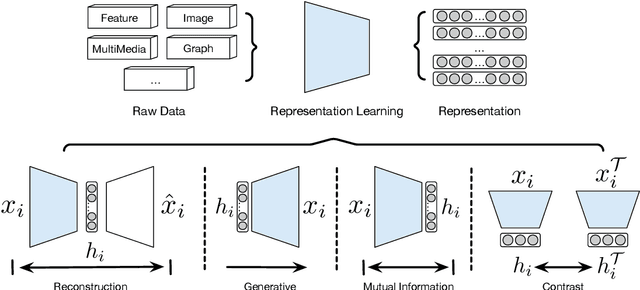
Clustering is a fundamental machine learning task which has been widely studied in the literature. Classic clustering methods follow the assumption that data are represented as features in a vectorized form through various representation learning techniques. As the data become increasingly complicated and complex, the shallow (traditional) clustering methods can no longer handle the high-dimensional data type. With the huge success of deep learning, especially the deep unsupervised learning, many representation learning techniques with deep architectures have been proposed in the past decade. Recently, the concept of Deep Clustering, i.e., jointly optimizing the representation learning and clustering, has been proposed and hence attracted growing attention in the community. Motivated by the tremendous success of deep learning in clustering, one of the most fundamental machine learning tasks, and the large number of recent advances in this direction, in this paper we conduct a comprehensive survey on deep clustering by proposing a new taxonomy of different state-of-the-art approaches. We summarize the essential components of deep clustering and categorize existing methods by the ways they design interactions between deep representation learning and clustering. Moreover, this survey also provides the popular benchmark datasets, evaluation metrics and open-source implementations to clearly illustrate various experimental settings. Last but not least, we discuss the practical applications of deep clustering and suggest challenging topics deserving further investigations as future directions.