Universal Inceptive GNNs by Eliminating the Smoothness-generalization Dilemma

Graph Neural Networks (GNNs) have demonstrated remarkable success in various domains, such as transaction and social net-works. However, their application is often hindered by the varyinghomophily levels across different orders of neighboring nodes, ne-cessitating separate model designs for homophilic and heterophilicgraphs. In this paper, we aim to develop a unified framework ca-pable of handling neighborhoods of various orders and homophilylevels. Through theoretical exploration, we identify a previouslyoverlooked architectural aspect in multi-hop learning: the cascadedependency, which leads to asmoothness-generalization dilemma.This dilemma significantly affects the learning process, especiallyin the context of high-order neighborhoods and heterophilic graphs.To resolve this issue, we propose an Inceptive Graph Neural Net-work (IGNN), a universal message-passing framework that replacesthe cascade dependency with an inceptive architecture. IGNN pro-vides independent representations for each hop, allowing personal-ized generalization capabilities, and captures neighborhood-wiserelationships to select appropriate receptive fields. Extensive ex-periments show that our IGNN outperforms 23 baseline methods,demonstrating superior performance on both homophilic and het-erophilic graphs, while also scaling efficiently to large graphs.

Heterophilous Distribution Propagation for Graph Neural Networks

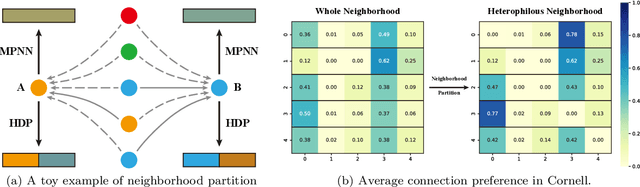
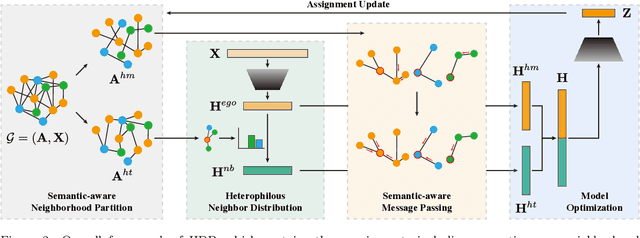
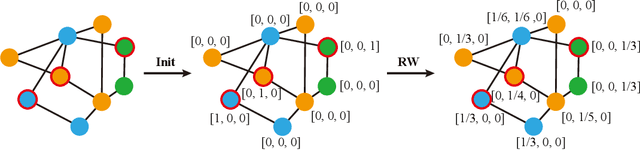
Graph Neural Networks (GNNs) have achieved remarkable success in various graph mining tasks by aggregating information from neighborhoods for representation learning. The success relies on the homophily assumption that nearby nodes exhibit similar behaviors, while it may be violated in many real-world graphs. Recently, heterophilous graph neural networks (HeterGNNs) have attracted increasing attention by modifying the neural message passing schema for heterophilous neighborhoods. However, they suffer from insufficient neighborhood partition and heterophily modeling, both of which are critical but challenging to break through. To tackle these challenges, in this paper, we propose heterophilous distribution propagation (HDP) for graph neural networks. Instead of aggregating information from all neighborhoods, HDP adaptively separates the neighbors into homophilous and heterphilous parts based on the pseudo assignments during training. The heterophilous neighborhood distribution is learned with orthogonality-oriented constraint via a trusted prototype contrastive learning paradigm. Both the homophilous and heterophilous patterns are propagated with a novel semantic-aware message passing mechanism. We conduct extensive experiments on 9 benchmark datasets with different levels of homophily. Experimental results show that our method outperforms representative baselines on heterophilous datasets.

Revisiting the Message Passing in Heterophilous Graph Neural Networks

Graph Neural Networks (GNNs) have demonstrated strong performance in graph mining tasks due to their message-passing mechanism, which is aligned with the homophily assumption that adjacent nodes exhibit similar behaviors. However, in many real-world graphs, connected nodes may display contrasting behaviors, termed as heterophilous patterns, which has attracted increased interest in heterophilous GNNs (HTGNNs). Although the message-passing mechanism seems unsuitable for heterophilous graphs due to the propagation of class-irrelevant information, it is still widely used in many existing HTGNNs and consistently achieves notable success. This raises the question: why does message passing remain effective on heterophilous graphs? To answer this question, in this paper, we revisit the message-passing mechanisms in heterophilous graph neural networks and reformulate them into a unified heterophilious message-passing (HTMP) mechanism. Based on HTMP and empirical analysis, we reveal that the success of message passing in existing HTGNNs is attributed to implicitly enhancing the compatibility matrix among classes. Moreover, we argue that the full potential of the compatibility matrix is not completely achieved due to the existence of incomplete and noisy semantic neighborhoods in real-world heterophilous graphs. To bridge this gap, we introduce a new approach named CMGNN, which operates within the HTMP mechanism to explicitly leverage and improve the compatibility matrix. A thorough evaluation involving 10 benchmark datasets and comparative analysis against 13 well-established baselines highlights the superior performance of the HTMP mechanism and CMGNN method.

A Survey on Graph Condensation

Analytics on large-scale graphs have posed significant challenges to computational efficiency and resource requirements. Recently, Graph condensation (GC) has emerged as a solution to address challenges arising from the escalating volume of graph data. The motivation of GC is to reduce the scale of large graphs to smaller ones while preserving essential information for downstream tasks. For a better understanding of GC and to distinguish it from other related topics, we present a formal definition of GC and establish a taxonomy that systematically categorizes existing methods into three types based on its objective, and classify the formulations to generate the condensed graphs into two categories as modifying the original graphs or synthetic completely new ones. Moreover, our survey includes a comprehensive analysis of datasets and evaluation metrics in this field. Finally, we conclude by addressing challenges and limitations, outlining future directions, and offering concise guidelines to inspire future research in this field.

A Comprehensive Survey on Deep Clustering: Taxonomy, Challenges, and Future Directions

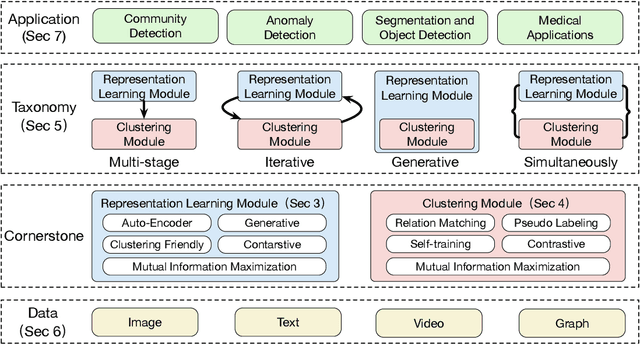
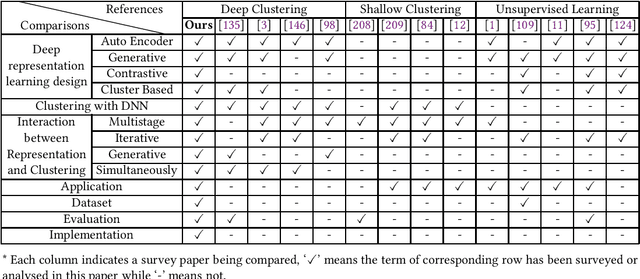
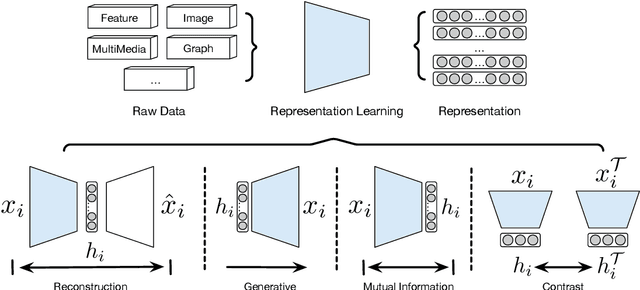
Clustering is a fundamental machine learning task which has been widely studied in the literature. Classic clustering methods follow the assumption that data are represented as features in a vectorized form through various representation learning techniques. As the data become increasingly complicated and complex, the shallow (traditional) clustering methods can no longer handle the high-dimensional data type. With the huge success of deep learning, especially the deep unsupervised learning, many representation learning techniques with deep architectures have been proposed in the past decade. Recently, the concept of Deep Clustering, i.e., jointly optimizing the representation learning and clustering, has been proposed and hence attracted growing attention in the community. Motivated by the tremendous success of deep learning in clustering, one of the most fundamental machine learning tasks, and the large number of recent advances in this direction, in this paper we conduct a comprehensive survey on deep clustering by proposing a new taxonomy of different state-of-the-art approaches. We summarize the essential components of deep clustering and categorize existing methods by the ways they design interactions between deep representation learning and clustering. Moreover, this survey also provides the popular benchmark datasets, evaluation metrics and open-source implementations to clearly illustrate various experimental settings. Last but not least, we discuss the practical applications of deep clustering and suggest challenging topics deserving further investigations as future directions.