Energy-Based Diffusion Language Models for Text Generation

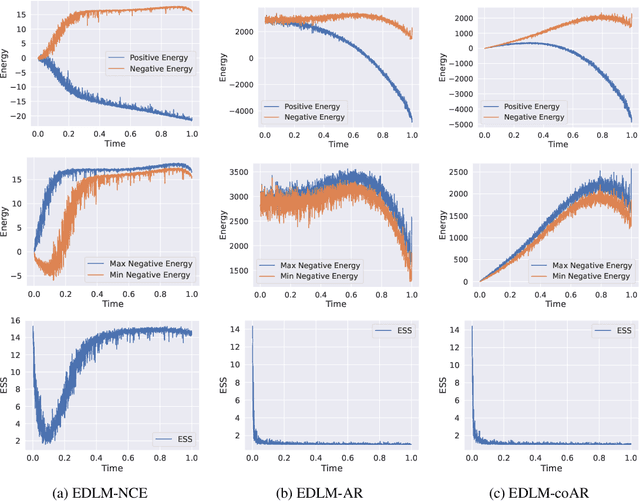
Despite remarkable progress in autoregressive language models, alternative generative paradigms beyond left-to-right generation are still being actively explored. Discrete diffusion models, with the capacity for parallel generation, have recently emerged as a promising alternative. Unfortunately, these models still underperform the autoregressive counterparts, with the performance gap increasing when reducing the number of sampling steps. Our analysis reveals that this degradation is a consequence of an imperfect approximation used by diffusion models. In this work, we propose Energy-based Diffusion Language Model (EDLM), an energy-based model operating at the full sequence level for each diffusion step, introduced to improve the underlying approximation used by diffusion models. More specifically, we introduce an EBM in a residual form, and show that its parameters can be obtained by leveraging a pretrained autoregressive model or by finetuning a bidirectional transformer via noise contrastive estimation. We also propose an efficient generation algorithm via parallel important sampling. Comprehensive experiments on language modeling benchmarks show that our model can consistently outperform state-of-the-art diffusion models by a significant margin, and approaches autoregressive models' perplexity. We further show that, without any generation performance drop, our framework offers a 1.3$\times$ sampling speedup over existing diffusion models.

Truncated Consistency Models

Consistency models have recently been introduced to accelerate sampling from diffusion models by directly predicting the solution (i.e., data) of the probability flow ODE (PF ODE) from initial noise. However, the training of consistency models requires learning to map all intermediate points along PF ODE trajectories to their corresponding endpoints. This task is much more challenging than the ultimate objective of one-step generation, which only concerns the PF ODE's noise-to-data mapping. We empirically find that this training paradigm limits the one-step generation performance of consistency models. To address this issue, we generalize consistency training to the truncated time range, which allows the model to ignore denoising tasks at earlier time steps and focus its capacity on generation. We propose a new parameterization of the consistency function and a two-stage training procedure that prevents the truncated-time training from collapsing to a trivial solution. Experiments on CIFAR-10 and ImageNet $64\times64$ datasets show that our method achieves better one-step and two-step FIDs than the state-of-the-art consistency models such as iCT-deep, using more than 2$\times$ smaller networks. Project page: https://truncated-cm.github.io/

Aligning Target-Aware Molecule Diffusion Models with Exact Energy Optimization

Generating ligand molecules for specific protein targets, known as structure-based drug design, is a fundamental problem in therapeutics development and biological discovery. Recently, target-aware generative models, especially diffusion models, have shown great promise in modeling protein-ligand interactions and generating candidate drugs. However, existing models primarily focus on learning the chemical distribution of all drug candidates, which lacks effective steerability on the chemical quality of model generations. In this paper, we propose a novel and general alignment framework to align pretrained target diffusion models with preferred functional properties, named AliDiff. AliDiff shifts the target-conditioned chemical distribution towards regions with higher binding affinity and structural rationality, specified by user-defined reward functions, via the preference optimization approach. To avoid the overfitting problem in common preference optimization objectives, we further develop an improved Exact Energy Preference Optimization method to yield an exact and efficient alignment of the diffusion models, and provide the closed-form expression for the converged distribution. Empirical studies on the CrossDocked2020 benchmark show that AliDiff can generate molecules with state-of-the-art binding energies with up to -7.07 Avg. Vina Score, while maintaining strong molecular properties.

A Dual Control Variate for doubly stochastic optimization and black-box variational inference

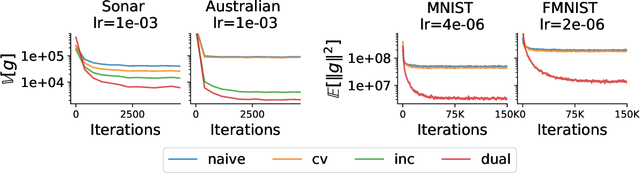
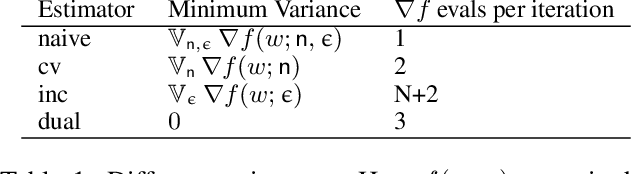
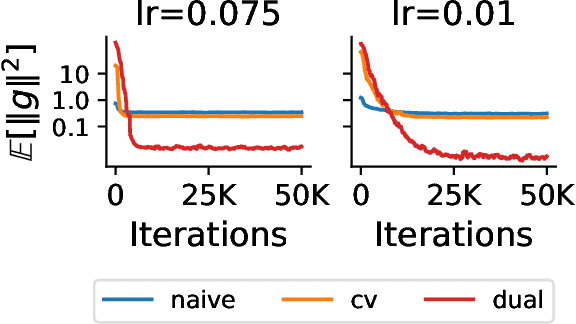
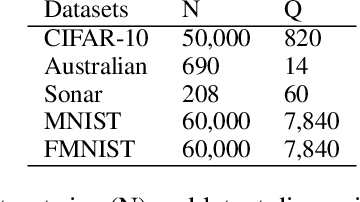
In this paper, we aim at reducing the variance of doubly stochastic optimization, a type of stochastic optimization algorithm that contains two independent sources of randomness: The subsampling of training data and the Monte Carlo estimation of expectations. Such an optimization regime often has the issue of large gradient variance which would lead to a slow rate of convergence. Therefore we propose Dual Control Variate, a new type of control variate capable of reducing gradient variance from both sources jointly. The dual control variate is built upon approximation-based control variates and incremental gradient methods. We show that on doubly stochastic optimization problems, compared with past variance reduction approaches that take only one source of randomness into account, dual control variate leads to a gradient estimator of significant smaller variance and demonstrates superior performance on real-world applications, like generalized linear models with dropout and black-box variational inference.

Score Modeling for Simulation-based Inference

Neural Posterior Estimation methods for simulation-based inference can be ill-suited for dealing with posterior distributions obtained by conditioning on multiple observations, as they may require a large number of simulator calls to yield accurate approximations. Neural Likelihood Estimation methods can naturally handle multiple observations, but require a separate inference step, which may affect their efficiency and performance. We introduce a new method for simulation-based inference that enjoys the benefits of both approaches. We propose to model the scores for the posterior distributions induced by individual observations, and introduce a sampling algorithm that combines the learned scores to approximately sample from the target efficiently.

Langevin Diffusion Variational Inference

Many methods that build powerful variational distributions based on unadjusted Langevin transitions exist. Most of these were developed using a wide range of different approaches and techniques. Unfortunately, the lack of a unified analysis and derivation makes developing new methods and reasoning about existing ones a challenging task. We address this giving a single analysis that unifies and generalizes these existing techniques. The main idea is to augment the target and variational by numerically simulating the underdamped Langevin diffusion process and its time reversal. The benefits of this approach are twofold: it provides a unified formulation for many existing methods, and it simplifies the development of new ones. In fact, using our formulation we propose a new method that combines the strengths of previously existing algorithms; it uses underdamped Langevin transitions and powerful augmentations parameterized by a score network. Our empirical evaluation shows that our proposed method consistently outperforms relevant baselines in a wide range of tasks.

Variational Inference with Locally Enhanced Bounds for Hierarchical Models

Hierarchical models represent a challenging setting for inference algorithms. MCMC methods struggle to scale to large models with many local variables and observations, and variational inference (VI) may fail to provide accurate approximations due to the use of simple variational families. Some variational methods (e.g. importance weighted VI) integrate Monte Carlo methods to give better accuracy, but these tend to be unsuitable for hierarchical models, as they do not allow for subsampling and their performance tends to degrade for high dimensional models. We propose a new family of variational bounds for hierarchical models, based on the application of tightening methods (e.g. importance weighting) separately for each group of local random variables. We show that our approach naturally allows the use of subsampling to get unbiased gradients, and that it fully leverages the power of methods that build tighter lower bounds by applying them independently in lower dimensional spaces, leading to better results and more accurate posterior approximations than relevant baselines.

Deep End-to-end Causal Inference

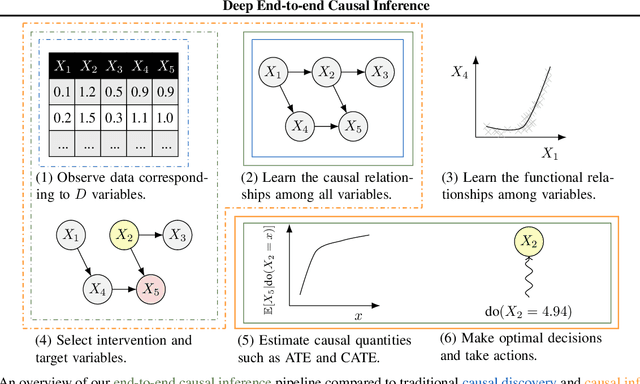
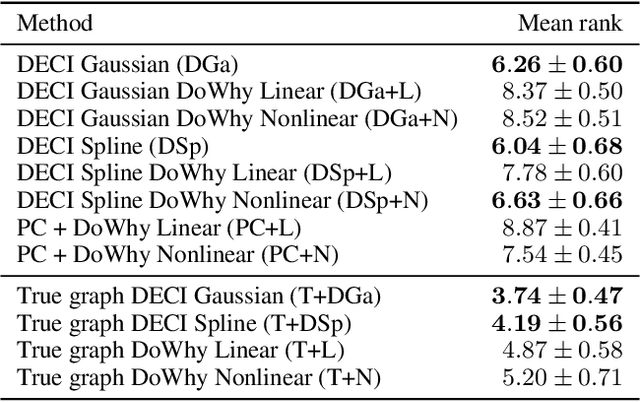
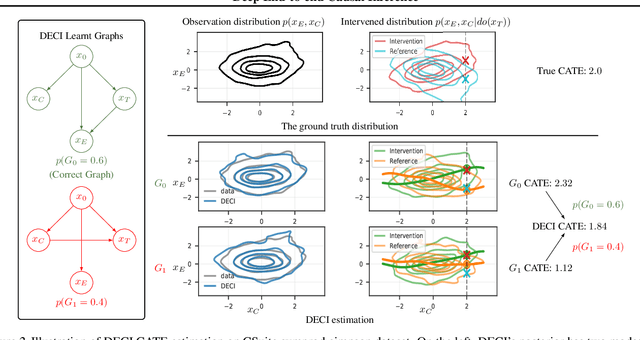
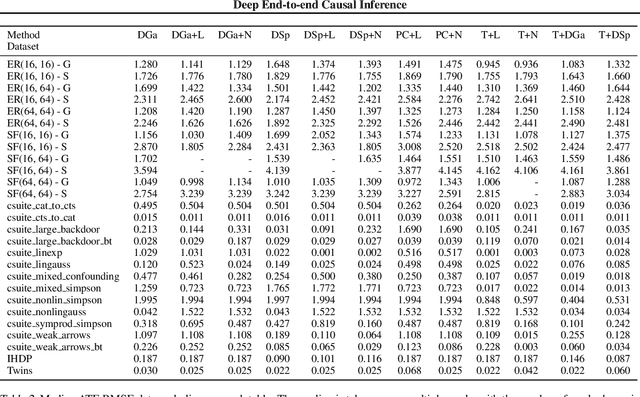
Causal inference is essential for data-driven decision making across domains such as business engagement, medical treatment or policy making. However, research on causal discovery and inference has evolved separately, and the combination of the two domains is not trivial. In this work, we develop Deep End-to-end Causal Inference (DECI), a single flow-based method that takes in observational data and can perform both causal discovery and inference, including conditional average treatment effect (CATE) estimation. We provide a theoretical guarantee that DECI can recover the ground truth causal graph under mild assumptions. In addition, our method can handle heterogeneous, real-world, mixed-type data with missing values, allowing for both continuous and discrete treatment decisions. Moreover, the design principle of our method can generalize beyond DECI, providing a general End-to-end Causal Inference (ECI) recipe, which enables different ECI frameworks to be built using existing methods. Our results show the superior performance of DECI when compared to relevant baselines for both causal discovery and (C)ATE estimation in over a thousand experiments on both synthetic datasets and other causal machine learning benchmark datasets.

MCMC Variational Inference via Uncorrected Hamiltonian Annealing

Given an unnormalized target distribution we want to obtain approximate samples from it and a tight lower bound on its (log) normalization constant log Z. Annealed Importance Sampling (AIS) with Hamiltonian MCMC is a powerful method that can be used to do this. Its main drawback is that it uses non-differentiable transition kernels, which makes tuning its many parameters hard. We propose a framework to use an AIS-like procedure with Uncorrected Hamiltonian MCMC, called Uncorrected Hamiltonian Annealing. Our method leads to tight and differentiable lower bounds on log Z. We show empirically that our method yields better performances than other competing approaches, and that the ability to tune its parameters using reparameterization gradients may lead to large performance improvements.

Empirical Evaluation of Biased Methods for Alpha Divergence Minimization

In this paper we empirically evaluate biased methods for alpha-divergence minimization. In particular, we focus on how the bias affects the final solutions found, and how this depends on the dimensionality of the problem. We find that (i) solutions returned by these methods appear to be strongly biased towards minimizers of the traditional "exclusive" KL-divergence, KL(q||p), and (ii) in high dimensions, an impractically large amount of computation is needed to mitigate this bias and obtain solutions that actually minimize the alpha-divergence of interest.