A Dual Control Variate for doubly stochastic optimization and black-box variational inference

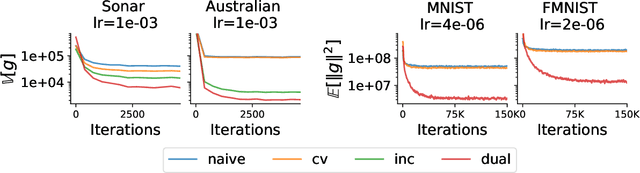
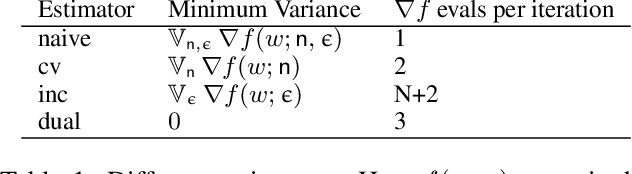
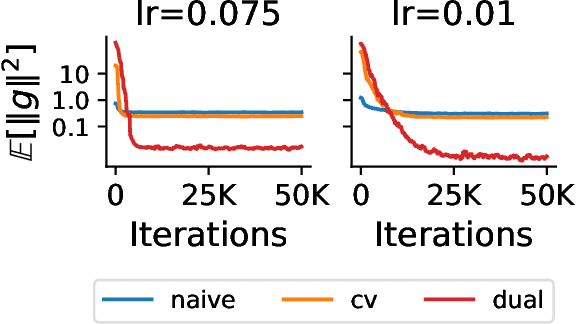
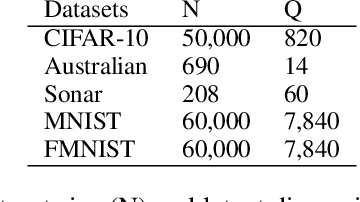
In this paper, we aim at reducing the variance of doubly stochastic optimization, a type of stochastic optimization algorithm that contains two independent sources of randomness: The subsampling of training data and the Monte Carlo estimation of expectations. Such an optimization regime often has the issue of large gradient variance which would lead to a slow rate of convergence. Therefore we propose Dual Control Variate, a new type of control variate capable of reducing gradient variance from both sources jointly. The dual control variate is built upon approximation-based control variates and incremental gradient methods. We show that on doubly stochastic optimization problems, compared with past variance reduction approaches that take only one source of randomness into account, dual control variate leads to a gradient estimator of significant smaller variance and demonstrates superior performance on real-world applications, like generalized linear models with dropout and black-box variational inference.