Scalable Bayesian Inference in the Era of Deep Learning: From Gaussian Processes to Deep Neural Networks

Large neural networks trained on large datasets have become the dominant paradigm in machine learning. These systems rely on maximum likelihood point estimates of their parameters, precluding them from expressing model uncertainty. This may result in overconfident predictions and it prevents the use of deep learning models for sequential decision making. This thesis develops scalable methods to equip neural networks with model uncertainty. In particular, we leverage the linearised Laplace approximation to equip pre-trained neural networks with the uncertainty estimates provided by their tangent linear models. This turns the problem of Bayesian inference in neural networks into one of Bayesian inference in conjugate Gaussian-linear models. Alas, the cost of this remains cubic in either the number of network parameters or in the number of observations times output dimensions. By assumption, neither are tractable. We address this intractability by using stochastic gradient descent (SGD) -- the workhorse algorithm of deep learning -- to perform posterior sampling in linear models and their convex duals: Gaussian processes. With this, we turn back to linearised neural networks, finding the linearised Laplace approximation to present a number of incompatibilities with modern deep learning practices -- namely, stochastic optimisation, early stopping and normalisation layers -- when used for hyperparameter learning. We resolve these and construct a sample-based EM algorithm for scalable hyperparameter learning with linearised neural networks. We apply the above methods to perform linearised neural network inference with ResNet-50 (25M parameters) trained on Imagenet (1.2M observations and 1000 output dimensions). Additionally, we apply our methods to estimate uncertainty for 3d tomographic reconstructions obtained with the deep image prior network.

Deep End-to-end Causal Inference

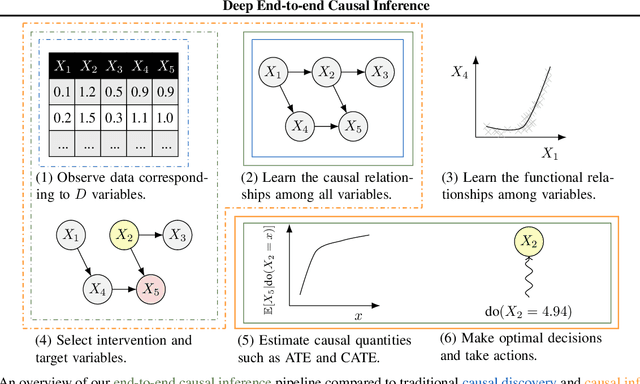
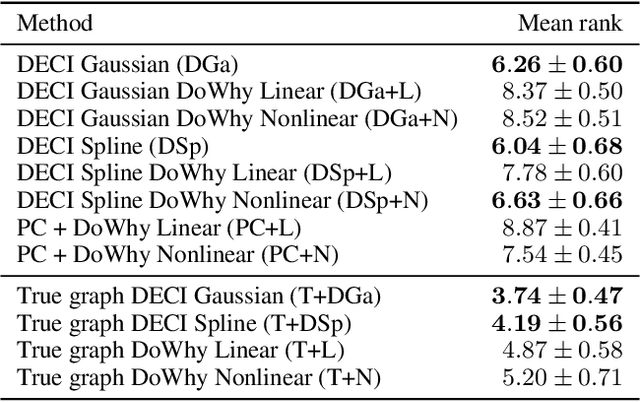
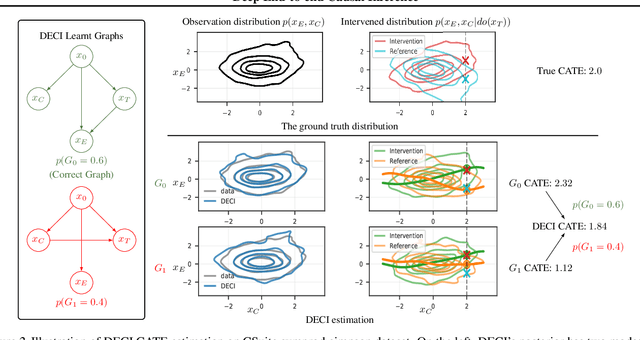
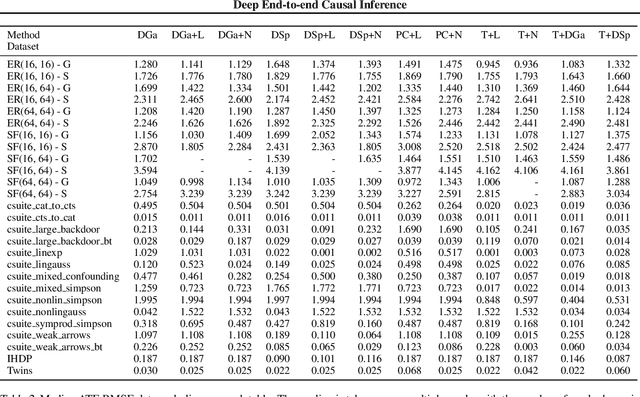
Causal inference is essential for data-driven decision making across domains such as business engagement, medical treatment or policy making. However, research on causal discovery and inference has evolved separately, and the combination of the two domains is not trivial. In this work, we develop Deep End-to-end Causal Inference (DECI), a single flow-based method that takes in observational data and can perform both causal discovery and inference, including conditional average treatment effect (CATE) estimation. We provide a theoretical guarantee that DECI can recover the ground truth causal graph under mild assumptions. In addition, our method can handle heterogeneous, real-world, mixed-type data with missing values, allowing for both continuous and discrete treatment decisions. Moreover, the design principle of our method can generalize beyond DECI, providing a general End-to-end Causal Inference (ECI) recipe, which enables different ECI frameworks to be built using existing methods. Our results show the superior performance of DECI when compared to relevant baselines for both causal discovery and (C)ATE estimation in over a thousand experiments on both synthetic datasets and other causal machine learning benchmark datasets.

Disentangling in Variational Autoencoders with Natural Clustering

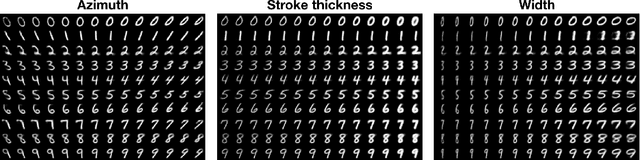
Learning representations that disentangle the underlying factors of variability in data is an intuitive precursor to AI with human-like reasoning. Consequently, it has been the object of many efforts of the machine learning community. This work takes a step further in this direction by addressing the scenario where generative factors present a multimodal distribution due to the existence of class distinction in the data. We formulate a lower bound on the joint distribution of inputs and class labels and present N-VAE, a model which is capable of separating factors of variation which are exclusive to certain classes from factors that are shared among classes. This model implements the natural clustering prior through the use of a class-conditioned latent space and a shared latent space. We show its usefulness for detecting and disentangling class-dependent generative factors as well as for generating rich artificial samples.