Heavy-Tailed Diffusion Models

Diffusion models achieve state-of-the-art generation quality across many applications, but their ability to capture rare or extreme events in heavy-tailed distributions remains unclear. In this work, we show that traditional diffusion and flow-matching models with standard Gaussian priors fail to capture heavy-tailed behavior. We address this by repurposing the diffusion framework for heavy-tail estimation using multivariate Student-t distributions. We develop a tailored perturbation kernel and derive the denoising posterior based on the conditional Student-t distribution for the backward process. Inspired by $\gamma$-divergence for heavy-tailed distributions, we derive a training objective for heavy-tailed denoisers. The resulting framework introduces controllable tail generation using only a single scalar hyperparameter, making it easily tunable for diverse real-world distributions. As specific instantiations of our framework, we introduce t-EDM and t-Flow, extensions of existing diffusion and flow models that employ a Student-t prior. Remarkably, our approach is readily compatible with standard Gaussian diffusion models and requires only minimal code changes. Empirically, we show that our t-EDM and t-Flow outperform standard diffusion models in heavy-tail estimation on high-resolution weather datasets in which generating rare and extreme events is crucial.

Kilometer-Scale Convection Allowing Model Emulation using Generative Diffusion Modeling

Storm-scale convection-allowing models (CAMs) are an important tool for predicting the evolution of thunderstorms and mesoscale convective systems that result in damaging extreme weather. By explicitly resolving convective dynamics within the atmosphere they afford meteorologists the nuance needed to provide outlook on hazard. Deep learning models have thus far not proven skilful at km-scale atmospheric simulation, despite being competitive at coarser resolution with state-of-the-art global, medium-range weather forecasting. We present a generative diffusion model called StormCast, which emulates the high-resolution rapid refresh (HRRR) model-NOAA's state-of-the-art 3km operational CAM. StormCast autoregressively predicts 99 state variables at km scale using a 1-hour time step, with dense vertical resolution in the atmospheric boundary layer, conditioned on 26 synoptic variables. We present evidence of successfully learnt km-scale dynamics including competitive 1-6 hour forecast skill for composite radar reflectivity alongside physically realistic convective cluster evolution, moist updrafts, and cold pool morphology. StormCast predictions maintain realistic power spectra for multiple predicted variables across multi-hour forecasts. Together, these results establish the potential for autoregressive ML to emulate CAMs -- opening up new km-scale frontiers for regional ML weather prediction and future climate hazard dynamical downscaling.

Huge Ensembles Part I: Design of Ensemble Weather Forecasts using Spherical Fourier Neural Operators

Studying low-likelihood high-impact extreme weather events in a warming world is a significant and challenging task for current ensemble forecasting systems. While these systems presently use up to 100 members, larger ensembles could enrich the sampling of internal variability. They may capture the long tails associated with climate hazards better than traditional ensemble sizes. Due to computational constraints, it is infeasible to generate huge ensembles (comprised of 1,000-10,000 members) with traditional, physics-based numerical models. In this two-part paper, we replace traditional numerical simulations with machine learning (ML) to generate hindcasts of huge ensembles. In Part I, we construct an ensemble weather forecasting system based on Spherical Fourier Neural Operators (SFNO), and we discuss important design decisions for constructing such an ensemble. The ensemble represents model uncertainty through perturbed-parameter techniques, and it represents initial condition uncertainty through bred vectors, which sample the fastest growing modes of the forecast. Using the European Centre for Medium-Range Weather Forecasts Integrated Forecasting System (IFS) as a baseline, we develop an evaluation pipeline composed of mean, spectral, and extreme diagnostics. Using large-scale, distributed SFNOs with 1.1 billion learned parameters, we achieve calibrated probabilistic forecasts. As the trajectories of the individual members diverge, the ML ensemble mean spectra degrade with lead time, consistent with physical expectations. However, the individual ensemble members' spectra stay constant with lead time. Therefore, these members simulate realistic weather states, and the ML ensemble thus passes a crucial spectral test in the literature. The IFS and ML ensembles have similar Extreme Forecast Indices, and we show that the ML extreme weather forecasts are reliable and discriminating.

Huge Ensembles Part II: Properties of a Huge Ensemble of Hindcasts Generated with Spherical Fourier Neural Operators

In Part I, we created an ensemble based on Spherical Fourier Neural Operators. As initial condition perturbations, we used bred vectors, and as model perturbations, we used multiple checkpoints trained independently from scratch. Based on diagnostics that assess the ensemble's physical fidelity, our ensemble has comparable performance to operational weather forecasting systems. However, it requires several orders of magnitude fewer computational resources. Here in Part II, we generate a huge ensemble (HENS), with 7,424 members initialized each day of summer 2023. We enumerate the technical requirements for running huge ensembles at this scale. HENS precisely samples the tails of the forecast distribution and presents a detailed sampling of internal variability. For extreme climate statistics, HENS samples events 4$\sigma$ away from the ensemble mean. At each grid cell, HENS improves the skill of the most accurate ensemble member and enhances coverage of possible future trajectories. As a weather forecasting model, HENS issues extreme weather forecasts with better uncertainty quantification. It also reduces the probability of outlier events, in which the verification value lies outside the ensemble forecast distribution.

Climate-Invariant Machine Learning

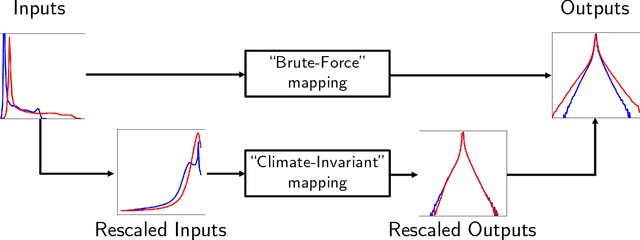
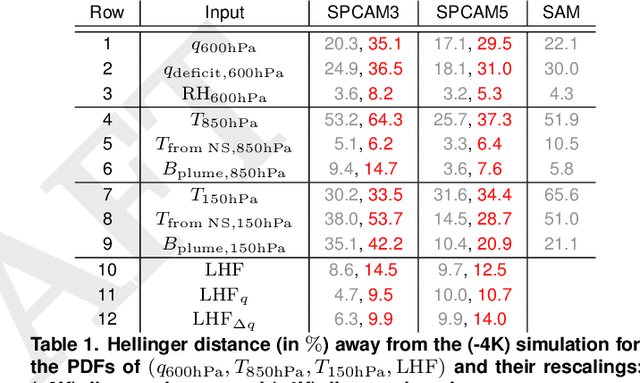
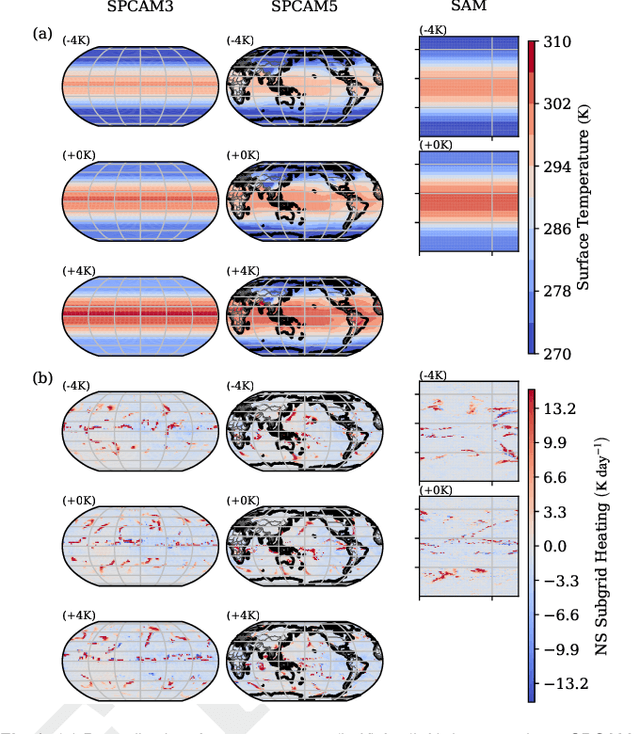
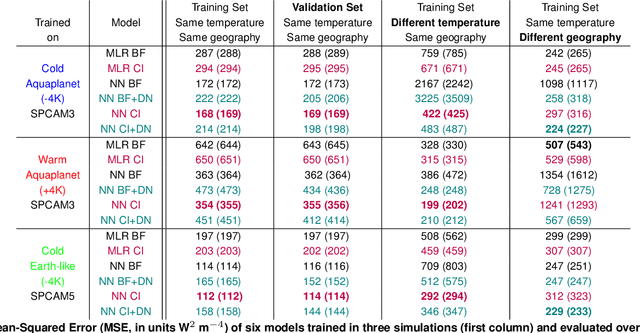
Data-driven algorithms, in particular neural networks, can emulate the effects of unresolved processes in coarse-resolution climate models when trained on high-resolution simulation data; however, they often make large generalization errors when evaluated in conditions they were not trained on. Here, we propose to physically rescale the inputs and outputs of machine learning algorithms to help them generalize to unseen climates. Applied to offline parameterizations of subgrid-scale thermodynamics in three distinct climate models, we show that rescaled or "climate-invariant" neural networks make accurate predictions in test climates that are 4K and 8K warmer than their training climates. Additionally, "climate-invariant" neural nets facilitate generalization between Aquaplanet and Earth-like simulations. Through visualization and attribution methods, we show that compared to standard machine learning models, "climate-invariant" algorithms learn more local and robust relations between storm-scale convection, radiation, and their synoptic thermodynamic environment. Overall, these results suggest that explicitly incorporating physical knowledge into data-driven models of Earth system processes can improve their consistency and ability to generalize across climate regimes.

Generative Modeling for Atmospheric Convection

To improve climate modeling, we need a better understanding of multi-scale atmospheric dynamics--the relationship between large scale environment and small-scale storm formation, morphology and propagation--as well as superior stochastic parameterization of convective organization. We analyze raw output from ~6 million instances of explicitly simulated convection spanning all global geographic regimes of convection in the tropics, focusing on the vertical velocities extracted every 15 minutes from ~4 hundred thousands separate instances of a storm-permitting moist turbulence model embedded within a multi-scale global model of the atmosphere. Generative modeling techniques applied on high-resolution climate data for representation learning hold the potential to drive next-generation parameterization and breakthroughs in understanding of convection and storm development. To that end, we design and implement a specialized Variational Autoencoder (VAE) to perform structural replication, dimensionality reduction and clustering on these cloud-resolving vertical velocity outputs. Our VAE reproduces the structure of disparate classes of convection, successfully capturing both their magnitude and variances. This VAE thus provides a novel way to perform unsupervised grouping of convective organization in multi-scale simulations of the atmosphere in a physically sensible manner. The success of our VAE in structural emulation, learning physical meaning in convective transitions and anomalous vertical velocity field detection may help set the stage for developing generative models for stochastic parameterization that might one day replace explicit convection calculations.

Towards Physically-consistent, Data-driven Models of Convection

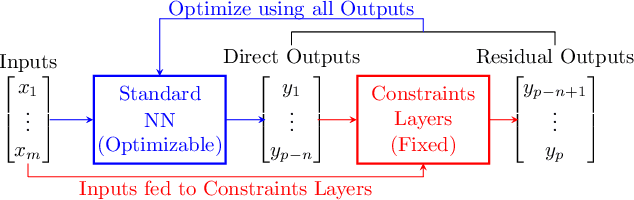
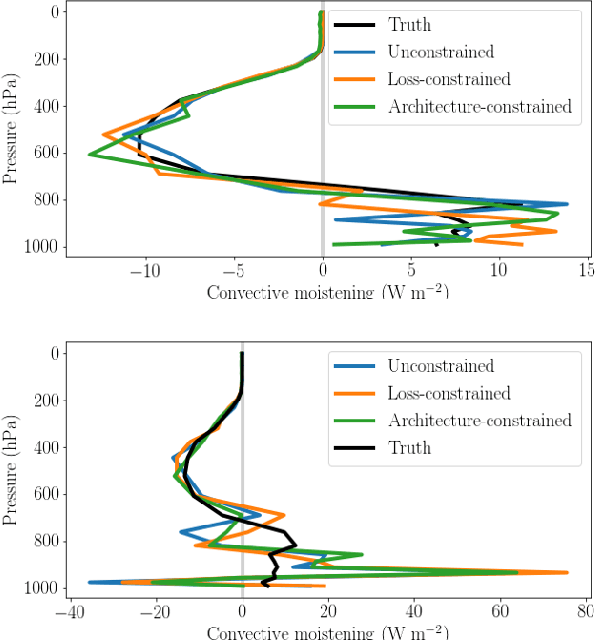
Data-driven algorithms, in particular neural networks, can emulate the effect of sub-grid scale processes in coarse-resolution climate models if trained on high-resolution climate simulations. However, they may violate key physical constraints and lack the ability to generalize outside of their training set. Here, we show that physical constraints can be enforced in neural networks, either approximately by adapting the loss function or to machine precision by adapting the architecture. As these physical constraints are insufficient to guarantee generalizability, we additionally propose a framework to find physical normalizations that can be applied to the training and validation data to improve the ability of neural networks to generalize to unseen climates.

Achieving Conservation of Energy in Neural Network Emulators for Climate Modeling

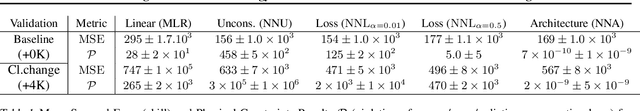
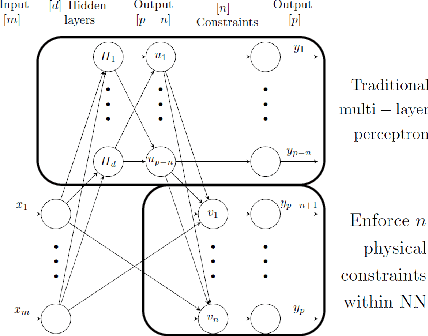
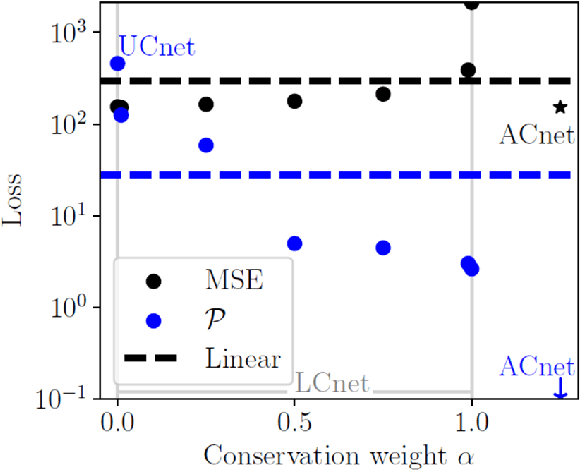
Artificial neural-networks have the potential to emulate cloud processes with higher accuracy than the semi-empirical emulators currently used in climate models. However, neural-network models do not intrinsically conserve energy and mass, which is an obstacle to using them for long-term climate predictions. Here, we propose two methods to enforce linear conservation laws in neural-network emulators of physical models: Constraining (1) the loss function or (2) the architecture of the network itself. Applied to the emulation of explicitly-resolved cloud processes in a prototype multi-scale climate model, we show that architecture constraints can enforce conservation laws to satisfactory numerical precision, while all constraints help the neural-network better generalize to conditions outside of its training set, such as global warming.