Large-Margin Classification with Multiple Decision Rules
Paper and Code
Nov 19, 2014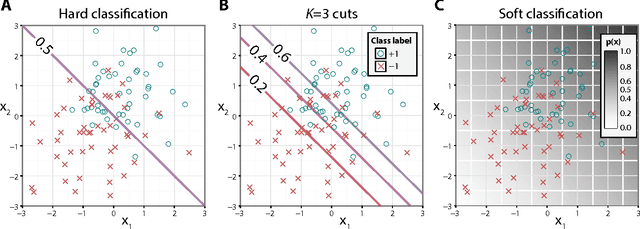
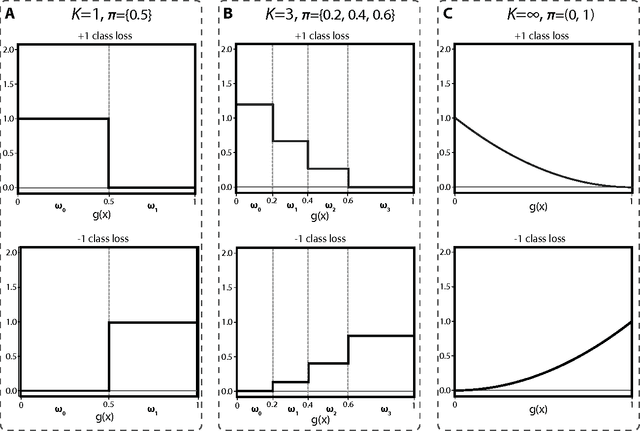
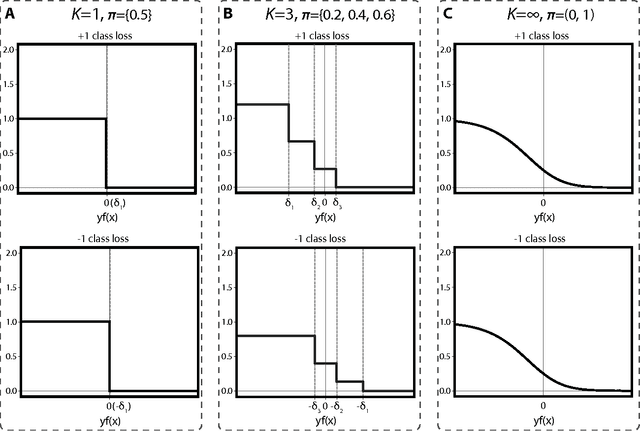
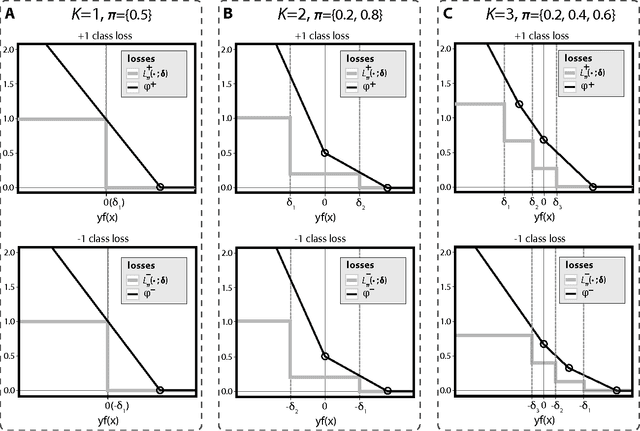
Binary classification is a common statistical learning problem in which a model is estimated on a set of covariates for some outcome indicating the membership of one of two classes. In the literature, there exists a distinction between hard and soft classification. In soft classification, the conditional class probability is modeled as a function of the covariates. In contrast, hard classification methods only target the optimal prediction boundary. While hard and soft classification methods have been studied extensively, not much work has been done to compare the actual tasks of hard and soft classification. In this paper we propose a spectrum of statistical learning problems which span the hard and soft classification tasks based on fitting multiple decision rules to the data. By doing so, we reveal a novel collection of learning tasks of increasing complexity. We study the problems using the framework of large-margin classifiers and a class of piecewise linear convex surrogates, for which we derive statistical properties and a corresponding sub-gradient descent algorithm. We conclude by applying our approach to simulation settings and a magnetic resonance imaging (MRI) dataset from the Alzheimer's Disease Neuroimaging Initiative (ADNI) study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge