Interior Object Geometry via Fitted Frames

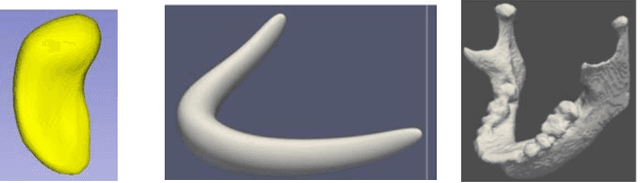
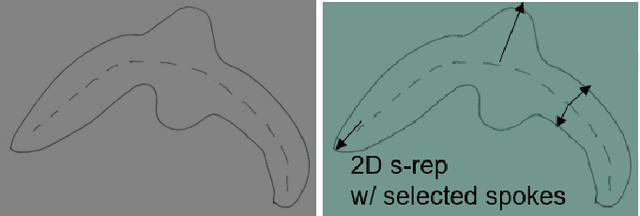
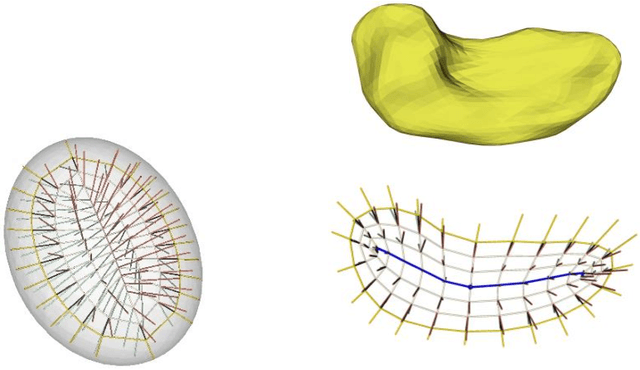
We describe a representation targeted for anatomic objects which is designed to enable strong locational correspondence within object populations and thus to provide powerful object statistics. The method generates fitted frames on the boundary and in the interior of objects and produces alignment-free geometric features from them. It accomplishes this by understanding an object as the diffeomorphic deformation of an ellipsoid and using a skeletal representation fitted throughout the deformation to produce a model of the target object, where the object is provided initially in the form of a boundary mesh. Via classification performance on hippocampi shape between individuals with a disorder vs. others, we compare our method to two state-of-the-art methods for producing object representations that are intended to capture geometric correspondence across a population of objects and to yield geometric features useful for statistics, and we show improved classification performance by this new representation, which we call the evolutionary s-rep. The geometric features that are derived from each of the representations, especially via fitted frames, is discussed.

Non-Euclidean Analysis of Joint Variations in Multi-Object Shapes

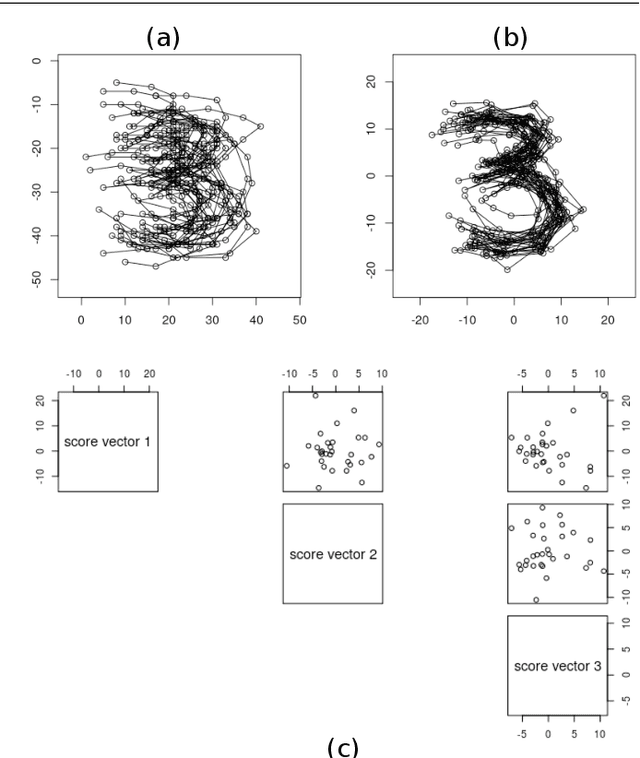
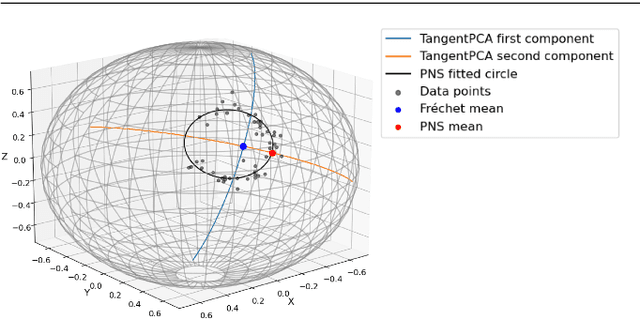
This paper considers joint analysis of multiple functionally related structures in classification tasks. In particular, our method developed is driven by how functionally correlated brain structures vary together between autism and control groups. To do so, we devised a method based on a novel combination of (1) non-Euclidean statistics that can faithfully represent non-Euclidean data in Euclidean spaces and (2) a non-parametric integrative analysis method that can decompose multi-block Euclidean data into joint, individual, and residual structures. We find that the resulting joint structure is effective, robust, and interpretable in recognizing the underlying patterns of the joint variation of multi-block non-Euclidean data. We verified the method in classifying the structural shape data collected from cases that developed and did not develop into Autistic Spectrum Disorder (ASD).

Rigidity Properties of the Blum Medial Axis

We consider the Blum medial axis of a region in $\mathbb R^n$ with piecewise smooth boundary and examine its "rigidity properties", by which we mean properties preserved under diffeomorphisms of the regions preserving the medial axis. There are several possible versions of rigidity depending on what features of the Blum medial axis we wish to retain. We use a form of the cross ratio from projective geometry to show that in the case of four smooth sheets of the medial axis meeting along a branching submanifold, the cross ratio defines a function on the branching sheet which must be preserved under any diffeomorphism of the medial axis with another. Second, we show in the generic case, along a Y-branching submanifold that there are three cross ratios involving the three limiting tangent planes of the three smooth sheets and each of the hyperplanes defined by one of the radial lines and the tangent space to the Y-branching submanifold at the point, which again must be preserved. Moreover, the triple of cross ratios then locally uniquely determines the angles between the smooth sheets. Third, we observe that for a diffeomorphism of the region preserving the Blum medial axis and the infinitesimal directions of the radial lines, the second derivative of the diffeomorphism at points of the medial axis must satisfy a condition relating the radial shape operators and hence the differential geometry of the boundaries at corresponding boundary points.

Modeling Multi-Object Configurations via Medial/Skeletal Linking Structures

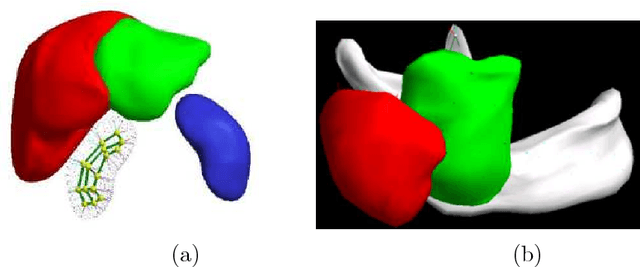
We introduce a method for modeling a configuration of objects in 2D or 3D images using a mathematical "skeletal linking structure" which will simultaneously capture the individual shape features of the objects and their positional information relative to one another. The objects may either have smooth boundaries and be disjoint from the others or share common portions of their boundaries with other objects in a piecewise smooth manner. These structures include a special class of "Blum medial linking structures," which are intrinsically associated to the configuration and build upon the Blum medial axes of the individual objects. We give a classification of the properties of Blum linking structures for generic configurations. The skeletal linking structures add increased flexibility for modeling configurations of objects by relaxing the Blum conditions and they extend in a minimal way the individual "skeletal structures" which have been previously used for modeling individual objects and capturing their geometric properties. This allows for the mathematical methods introduced for single objects to be significantly extended to the entire configuration of objects. These methods not only capture the internal shape structures of the individual objects but also the external structure of the neighboring regions of the objects.

Shape and Positional Geometry of Multi-Object Configurations

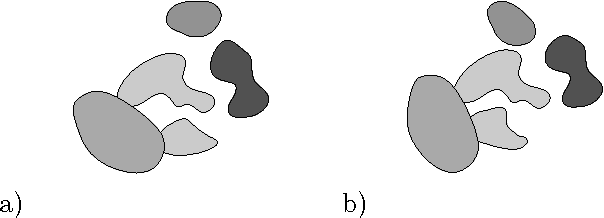
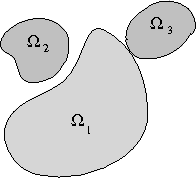
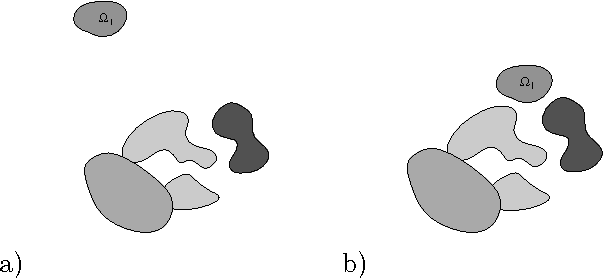
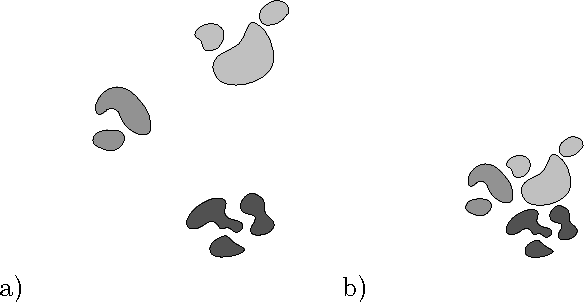
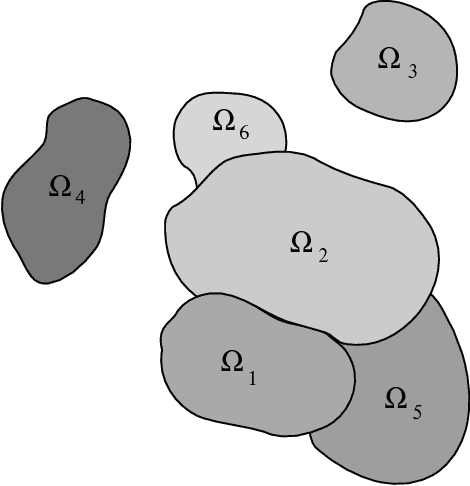
In previous work, we introduced a method for modeling a configuration of objects in 2D and 3D images using a mathematical "medial/skeletal linking structure." In this paper, we show how these structures allow us to capture positional properties of a multi-object configuration in addition to the shape properties of the individual objects. In particular, we introduce numerical invariants for positional properties which measure the closeness of neighboring objects, including identifying the parts of the objects which are close, and the "relative significance" of objects compared with the other objects in the configuration. Using these numerical measures, we introduce a hierarchical ordering and relations between the individual objects, and quantitative criteria for identifying subconfigurations. In addition, the invariants provide a "proximity matrix" which yields a unique set of weightings measuring overall proximity of objects in the configuration. Furthermore, we show that these invariants, which are volumetrically defined and involve external regions, may be computed via integral formulas in terms of "skeletal linking integrals" defined on the internal skeletal structures of the objects.