Modeling Multi-Object Configurations via Medial/Skeletal Linking Structures

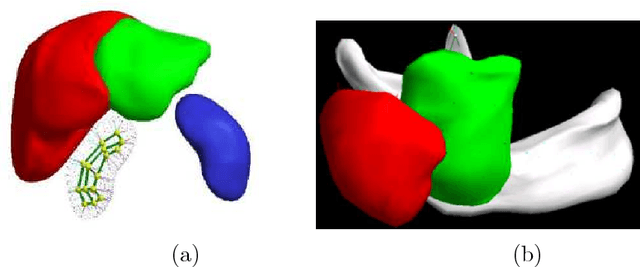
We introduce a method for modeling a configuration of objects in 2D or 3D images using a mathematical "skeletal linking structure" which will simultaneously capture the individual shape features of the objects and their positional information relative to one another. The objects may either have smooth boundaries and be disjoint from the others or share common portions of their boundaries with other objects in a piecewise smooth manner. These structures include a special class of "Blum medial linking structures," which are intrinsically associated to the configuration and build upon the Blum medial axes of the individual objects. We give a classification of the properties of Blum linking structures for generic configurations. The skeletal linking structures add increased flexibility for modeling configurations of objects by relaxing the Blum conditions and they extend in a minimal way the individual "skeletal structures" which have been previously used for modeling individual objects and capturing their geometric properties. This allows for the mathematical methods introduced for single objects to be significantly extended to the entire configuration of objects. These methods not only capture the internal shape structures of the individual objects but also the external structure of the neighboring regions of the objects.

Shape and Positional Geometry of Multi-Object Configurations

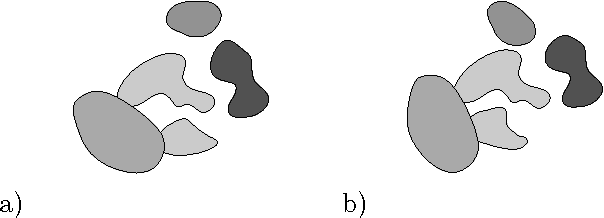
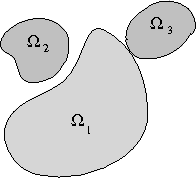
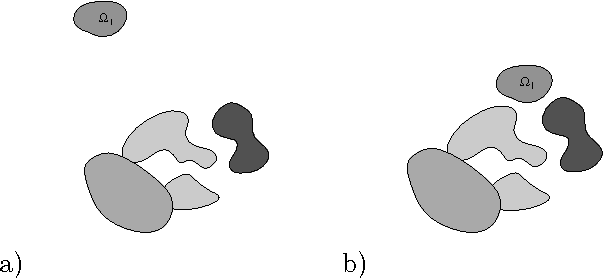
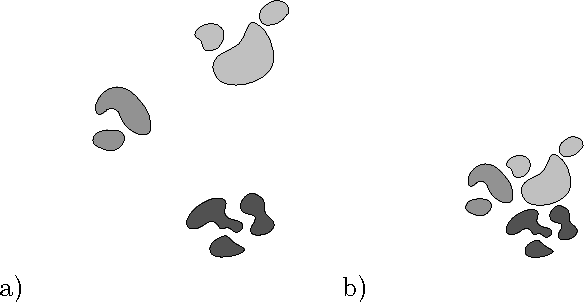
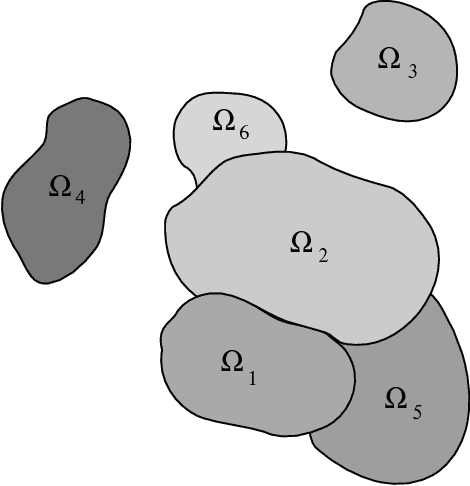
In previous work, we introduced a method for modeling a configuration of objects in 2D and 3D images using a mathematical "medial/skeletal linking structure." In this paper, we show how these structures allow us to capture positional properties of a multi-object configuration in addition to the shape properties of the individual objects. In particular, we introduce numerical invariants for positional properties which measure the closeness of neighboring objects, including identifying the parts of the objects which are close, and the "relative significance" of objects compared with the other objects in the configuration. Using these numerical measures, we introduce a hierarchical ordering and relations between the individual objects, and quantitative criteria for identifying subconfigurations. In addition, the invariants provide a "proximity matrix" which yields a unique set of weightings measuring overall proximity of objects in the configuration. Furthermore, we show that these invariants, which are volumetrically defined and involve external regions, may be computed via integral formulas in terms of "skeletal linking integrals" defined on the internal skeletal structures of the objects.

Multi-Scale Local Shape Analysis and Feature Selection in Machine Learning Applications

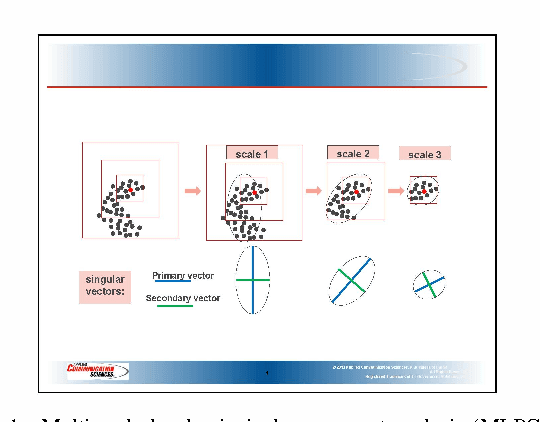
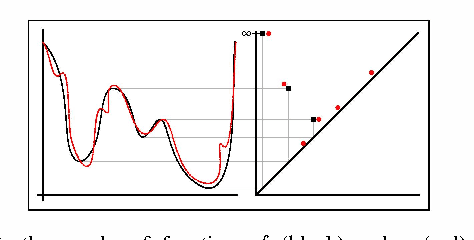
We introduce a method called multi-scale local shape analysis, or MLSA, for extracting features that describe the local structure of points within a dataset. The method uses both geometric and topological features at multiple levels of granularity to capture diverse types of local information for subsequent machine learning algorithms operating on the dataset. Using synthetic and real dataset examples, we demonstrate significant performance improvement of classification algorithms constructed for these datasets with correspondingly augmented features.