Paul Bendich
Topological Parallax: A Geometric Specification for Deep Perception Models
Jun 20, 2023



Abstract:For safety and robustness of AI systems, we introduce topological parallax as a theoretical and computational tool that compares a trained model to a reference dataset to determine whether they have similar multiscale geometric structure. Our proofs and examples show that this geometric similarity between dataset and model is essential to trustworthy interpolation and perturbation, and we conjecture that this new concept will add value to the current debate regarding the unclear relationship between overfitting and generalization in applications of deep-learning. In typical DNN applications, an explicit geometric description of the model is impossible, but parallax can estimate topological features (components, cycles, voids, etc.) in the model by examining the effect on the Rips complex of geodesic distortions using the reference dataset. Thus, parallax indicates whether the model shares similar multiscale geometric features with the dataset. Parallax presents theoretically via topological data analysis [TDA] as a bi-filtered persistence module, and the key properties of this module are stable under perturbation of the reference dataset.
A Convolutional Persistence Transform
Aug 03, 2022



Abstract:We consider a new topological feauturization of $d$-dimensional images, obtained by convolving images with various filters before computing persistence. Viewing a convolution filter as a motif within an image, the persistence diagram of the resulting convolution describes the way the motif is distributed throughout that image. This pipeline, which we call convolutional persistence, extends the capacity of topology to observe patterns in image data. Indeed, we prove that (generically speaking) for any two images one can find some filter for which they produce different persistence diagrams, so that the collection of all possible convolutional persistence diagrams for a given image is an injective invariant. This is proven by showing convolutional persistence to be a special case of another topological invariant, the Persistent Homology Transform. Other advantages of convolutional persistence are improved stability and robustness to noise, greater flexibility for data-dependent vectorizations, and reduced computational complexity for convolutions with large stride vectors. Additionally, we have a suite of experiments showing that convolutions greatly improve the predictive power of persistence on a host of classification tasks, even if one uses random filters and vectorizes the resulting diagrams by recording only their total persistences.
Improving Metric Dimensionality Reduction with Distributed Topology
Jun 14, 2021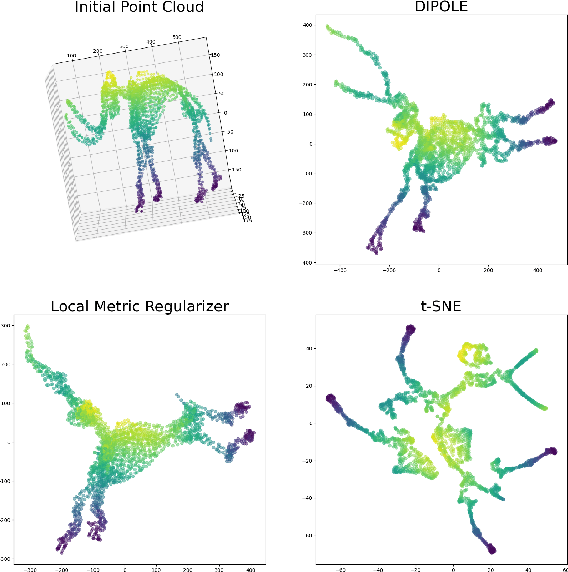
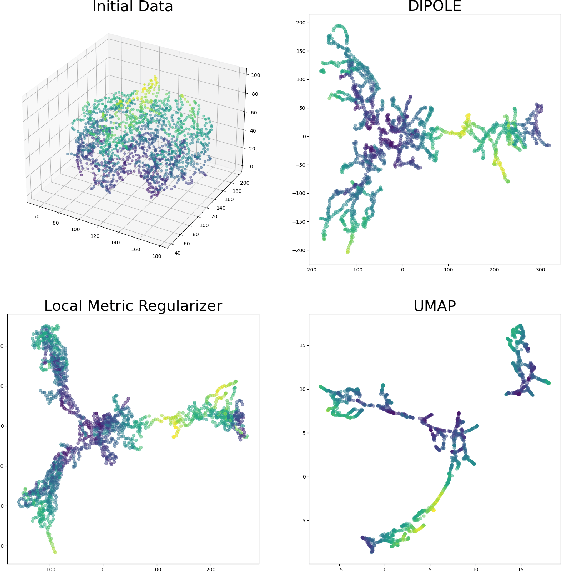
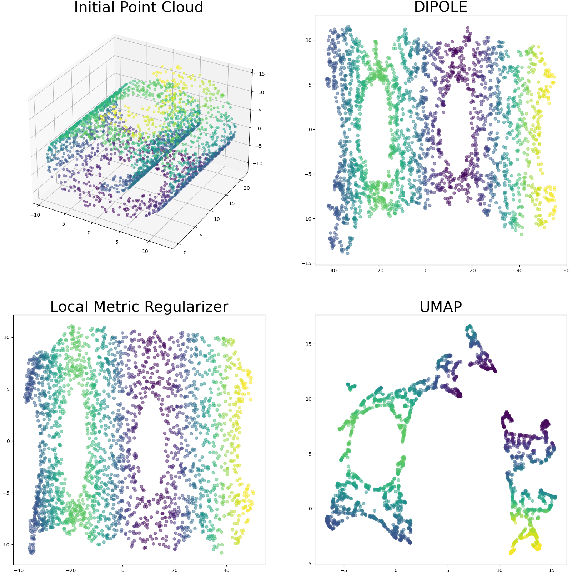
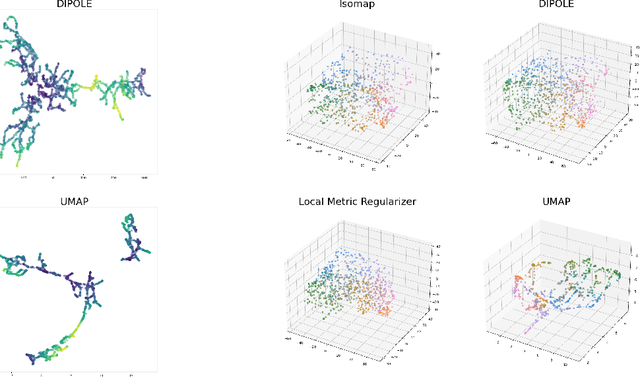
Abstract:We propose a novel approach to dimensionality reduction combining techniques of metric geometry and distributed persistent homology, in the form of a gradient-descent based method called DIPOLE. DIPOLE is a dimensionality-reduction post-processing step that corrects an initial embedding by minimizing a loss functional with both a local, metric term and a global, topological term. By fixing an initial embedding method (we use Isomap), DIPOLE can also be viewed as a full dimensionality-reduction pipeline. This framework is based on the strong theoretical and computational properties of distributed persistent homology and comes with the guarantee of almost sure convergence. We observe that DIPOLE outperforms popular methods like UMAP, t-SNE, and Isomap on a number of popular datasets, both visually and in terms of precise quantitative metrics.
From Geometry to Topology: Inverse Theorems for Distributed Persistence
Feb 03, 2021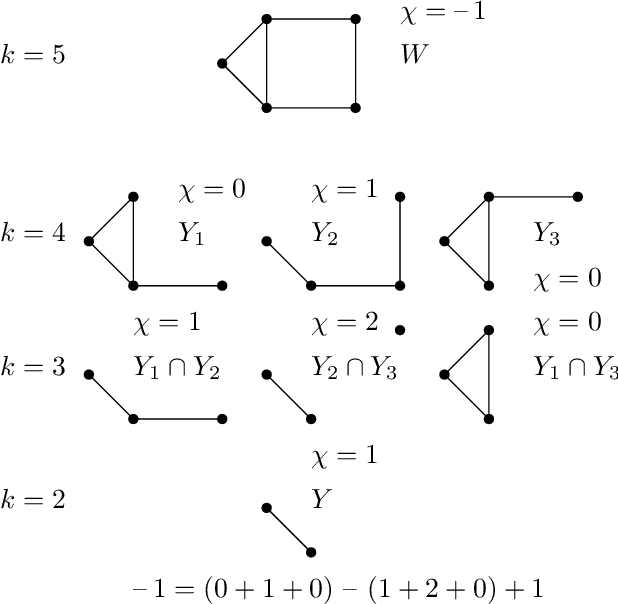
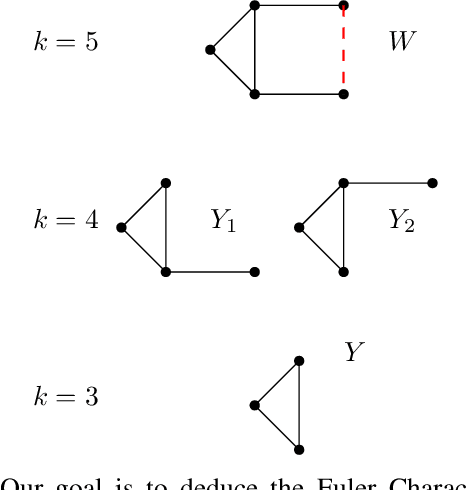
Abstract:What is the "right" topological invariant of a large point cloud X? Prior research has focused on estimating the full persistence diagram of X, a quantity that is very expensive to compute, unstable to outliers, and far from a sufficient statistic. We therefore propose that the correct invariant is not the persistence diagram of X, but rather the collection of persistence diagrams of many small subsets. This invariant, which we call "distributed persistence," is trivially parallelizable, more stable to outliers, and has a rich inverse theory. The map from the space of point clouds (with the quasi-isometry metric) to the space of distributed persistence invariants (with the Hausdorff-Bottleneck distance) is a global quasi-isometry. This is a much stronger property than simply being injective, as it implies that the inverse of a small neighborhood is a small neighborhood, and is to our knowledge the only result of its kind in the TDA literature. Moreover, the quasi-isometry bounds depend on the size of the subsets taken, so that as the size of these subsets goes from small to large, the invariant interpolates between a purely geometric one and a topological one. Lastly, we note that our inverse results do not actually require considering all subsets of a fixed size (an enormous collection), but a relatively small collection satisfying certain covering properties that arise with high probability when randomly sampling subsets. These theoretical results are complemented by two synthetic experiments demonstrating the use of distributed persistence in practice.
A Fast and Robust Method for Global Topological Functional Optimization
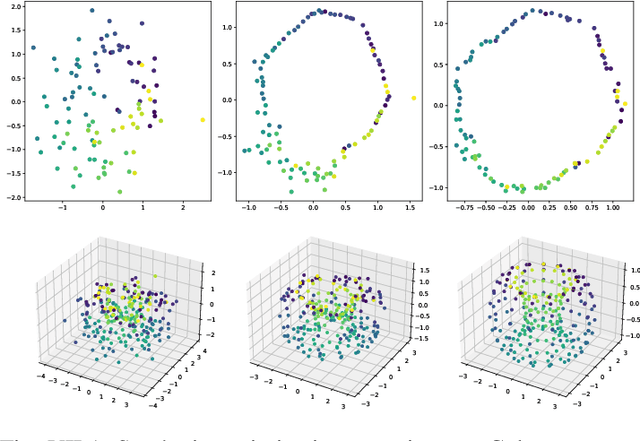
Sep 17, 2020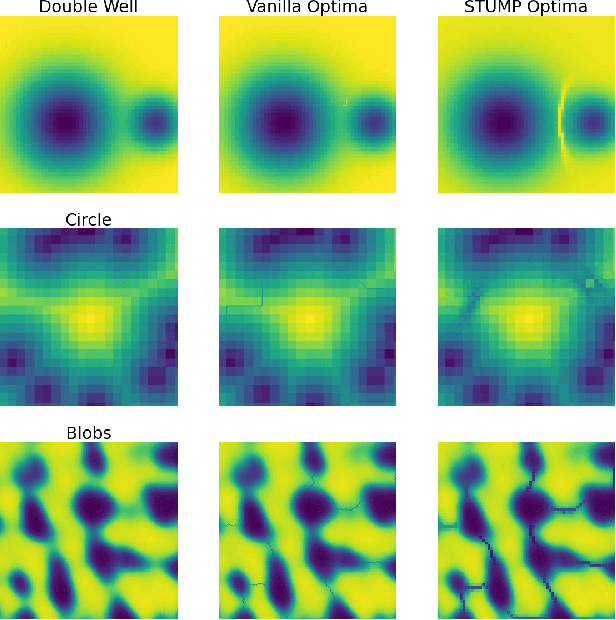
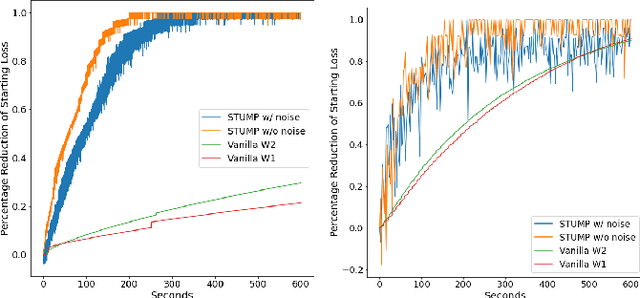
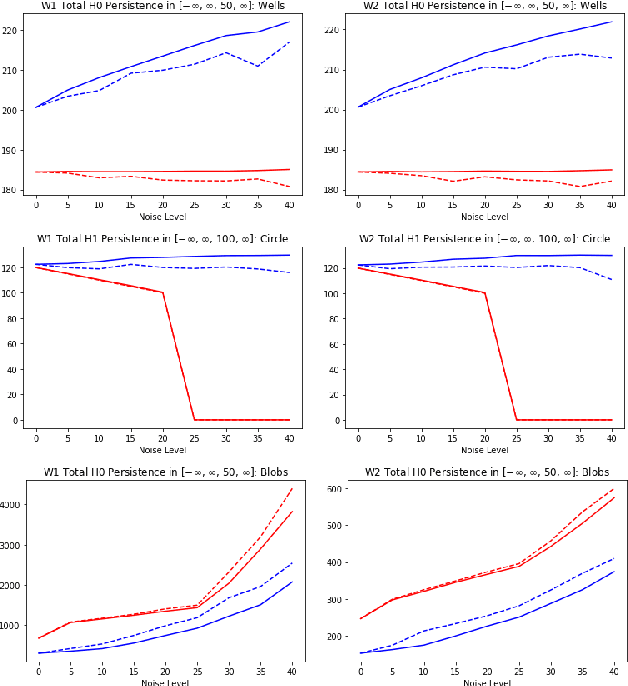
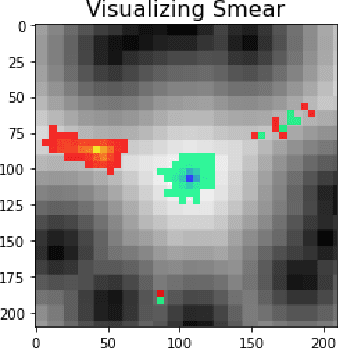
Abstract:Topological statistics, in the form of persistence diagrams, are a class of shape descriptors that capture global structural information in data. The mapping from data structures to persistence diagrams is almost everywhere differentiable, allowing for topological gradients to be backpropagated to ordinary gradients. However, as a method for optimizing a topological functional, this backpropagation method is expensive, unstable, and produces very fragile optima. Our contribution is to introduce a novel backpropagation scheme that is significantly faster, more stable, and produces more robust optima. Moreover, this scheme can also be used to produce a stable visualization of dots in a persistence diagram as a distribution over critical, and near-critical, simplices in the data structure.
Geometric Fusion via Joint Delay Embeddings
Feb 25, 2020Abstract:We introduce geometric and topological methods to develop a new framework for fusing multi-sensor time series. This framework consists of two steps: (1) a joint delay embedding, which reconstructs a high-dimensional state space in which our sensors correspond to observation functions, and (2) a simple orthogonalization scheme, which accounts for tangencies between such observation functions, and produces a more diversified geometry on the embedding space. We conclude with some synthetic and real-world experiments demonstrating that our framework outperforms traditional metric fusion methods.
Graph Spectral Embedding for Parsimonious Transmission of Multivariate Time Series
Oct 10, 2019



Abstract:We propose a graph spectral representation of time series data that 1) is parsimoniously encoded to user-demanded resolution; 2) is unsupervised and performant in data-constrained scenarios; 3) captures event and event-transition structure within the time series; and 4) has near-linear computational complexity in both signal length and ambient dimension. This representation, which we call Laplacian Events Signal Segmentation (LESS), can be computed on time series of arbitrary dimension and originating from sensors of arbitrary type. Hence, time series originating from sensors of heterogeneous type can be compressed to levels demanded by constrained-communication environments, before being fused at a common center. Temporal dynamics of the data is summarized without explicit partitioning or probabilistic modeling. As a proof-of-principle, we apply this technique on high dimensional wavelet coefficients computed from the Free Spoken Digit Dataset to generate a memory efficient representation that is interpretable. Due to its unsupervised and non-parametric nature, LESS representations remain performant in the digit classification task despite the absence of labels and limited data.
Multi-scale Geometric Summaries for Similarity-based Sensor Fusion
Oct 13, 2018



Abstract:In this work, we address fusion of heterogeneous sensor data using wavelet-based summaries of fused self-similarity information from each sensor. The technique we develop is quite general, does not require domain specific knowledge or physical models, and requires no training. Nonetheless, it can perform surprisingly well at the general task of differentiating classes of time-ordered behavior sequences which are sensed by more than one modality. As a demonstration of our capabilities in the audio to video context, we focus on the differentiation of speech sequences. Data from two or more modalities first are represented using self-similarity matrices(SSMs) corresponding to time-ordered point clouds in feature spaces of each of these data sources; we note that these feature spaces can be of entirely different scale and dimensionality. A fused similarity template is then derived from the modality-specific SSMs using a technique called similarity network fusion (SNF). We investigate pipelines using SNF as both an upstream (feature-level) and a downstream (ranking-level) fusion technique. Multiscale geometric features of this template are then extracted using a recently-developed technique called the scattering transform, and these features are then used to differentiate speech sequences. This method outperforms unsupervised techniques which operate directly on the raw data, and it also outperforms stovepiped methods which operate on SSMs separately derived from the distinct modalities. The benefits of this method become even more apparent as the simulated peak signal to noise ratio decreases.
Supervised Learning of Labeled Pointcloud Differences via Cover-Tree Entropy Reduction
Jan 19, 2018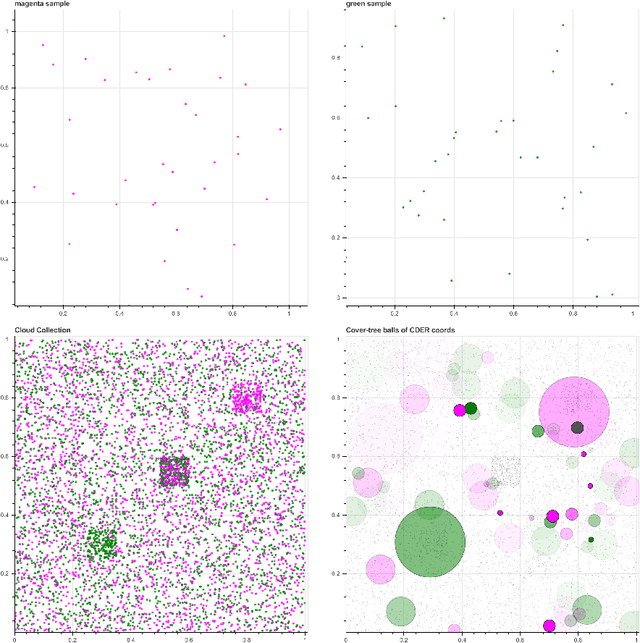
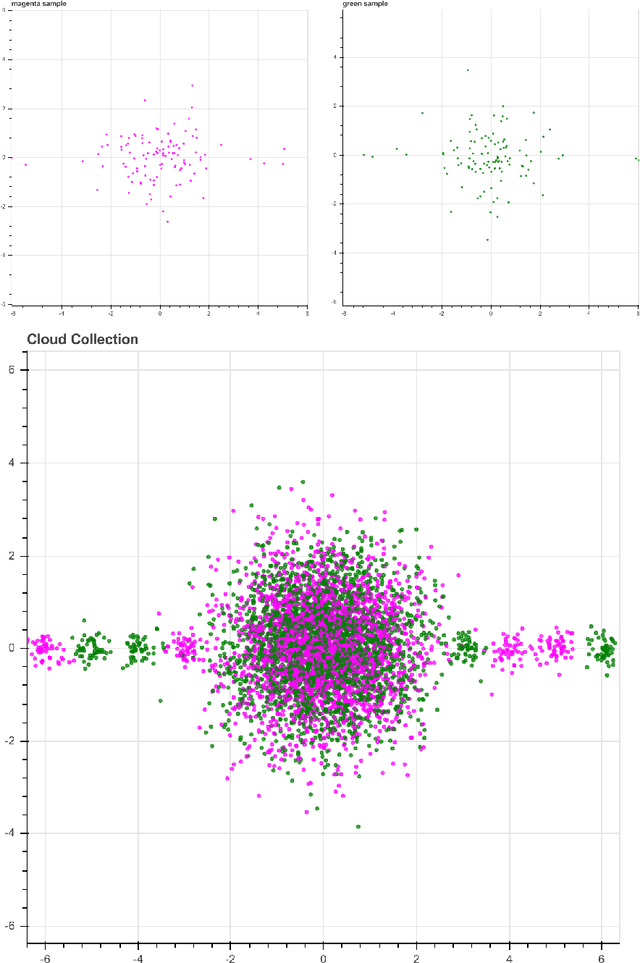
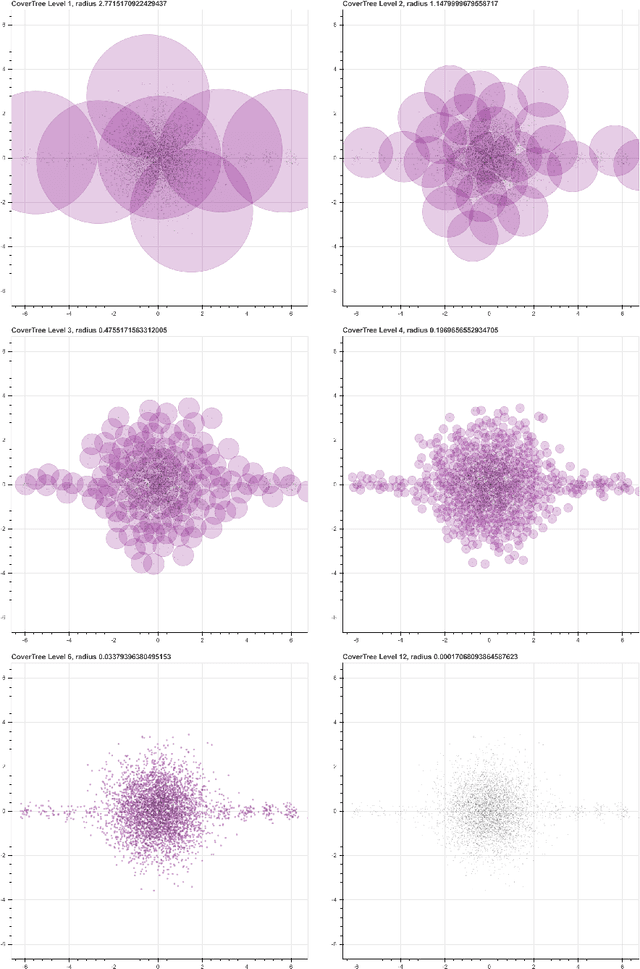
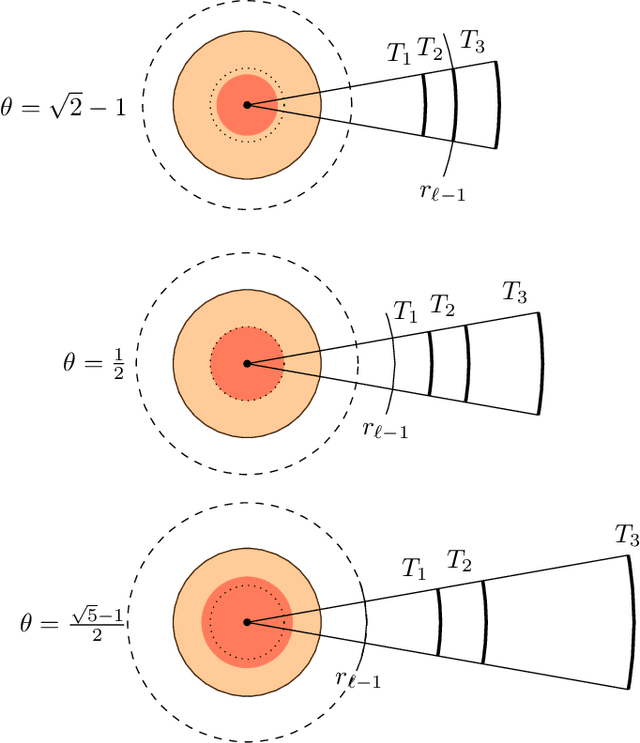
Abstract:We introduce a new algorithm, called CDER, for supervised machine learning that merges the multi-scale geometric properties of Cover Trees with the information-theoretic properties of entropy. CDER applies to a training set of labeled pointclouds embedded in a common Euclidean space. If typical pointclouds corresponding to distinct labels tend to differ at any scale in any sub-region, CDER can identify these differences in (typically) linear time, creating a set of distributional coordinates which act as a feature extraction mechanism for supervised learning. We describe theoretical properties and implementation details of CDER, and illustrate its benefits on several synthetic examples.
Geometric Cross-Modal Comparison of Heterogeneous Sensor Data
Nov 23, 2017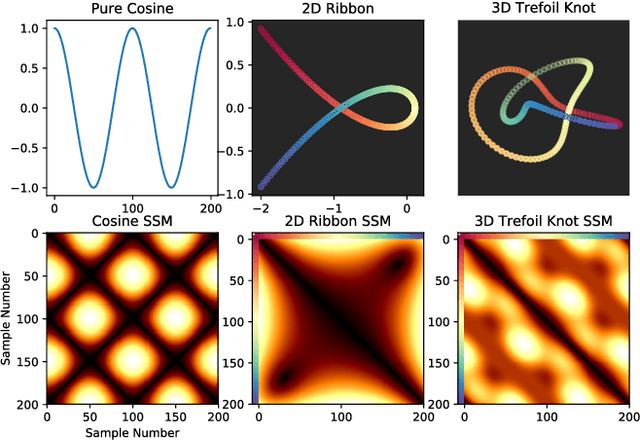
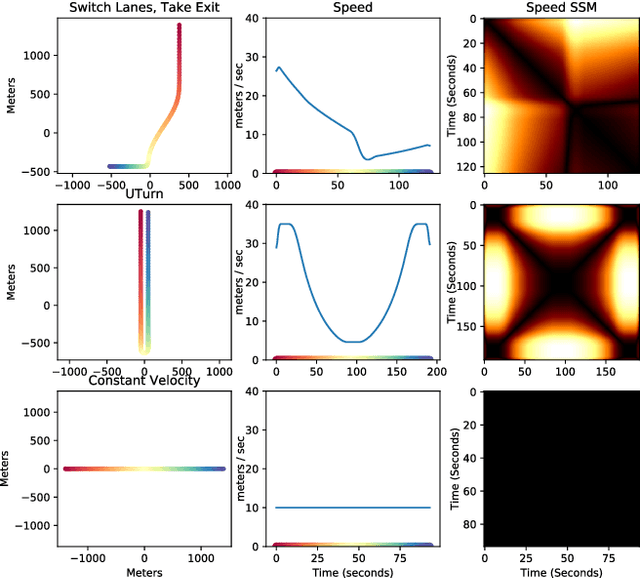
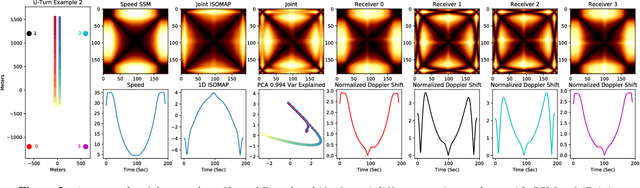
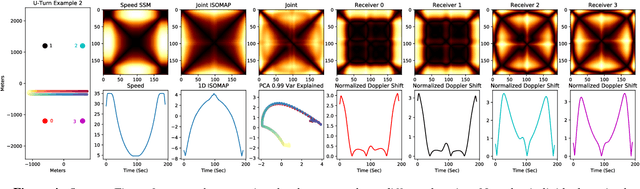
Abstract:In this work, we address the problem of cross-modal comparison of aerial data streams. A variety of simulated automobile trajectories are sensed using two different modalities: full-motion video, and radio-frequency (RF) signals received by detectors at various locations. The information represented by the two modalities is compared using self-similarity matrices (SSMs) corresponding to time-ordered point clouds in feature spaces of each of these data sources; we note that these feature spaces can be of entirely different scale and dimensionality. Several metrics for comparing SSMs are explored, including a cutting-edge time-warping technique that can simultaneously handle local time warping and partial matches, while also controlling for the change in geometry between feature spaces of the two modalities. We note that this technique is quite general, and does not depend on the choice of modalities. In this particular setting, we demonstrate that the cross-modal distance between SSMs corresponding to the same trajectory type is smaller than the cross-modal distance between SSMs corresponding to distinct trajectory types, and we formalize this observation via precision-recall metrics in experiments. Finally, we comment on promising implications of these ideas for future integration into multiple-hypothesis tracking systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge