Supervised Learning of Labeled Pointcloud Differences via Cover-Tree Entropy Reduction

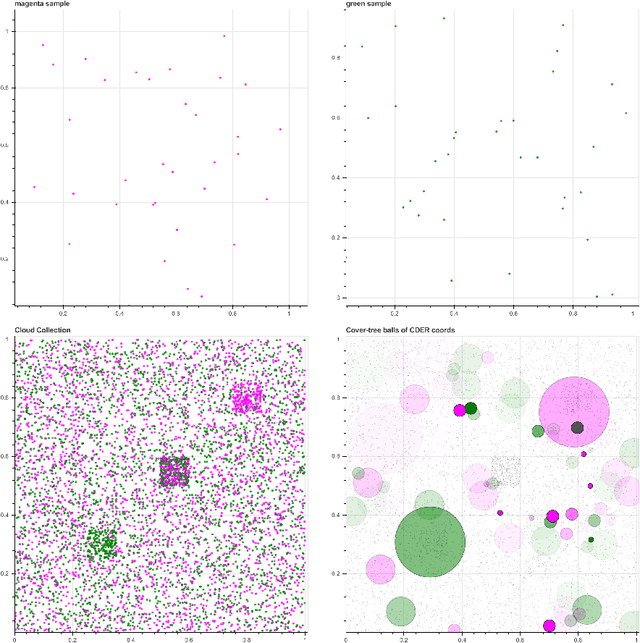
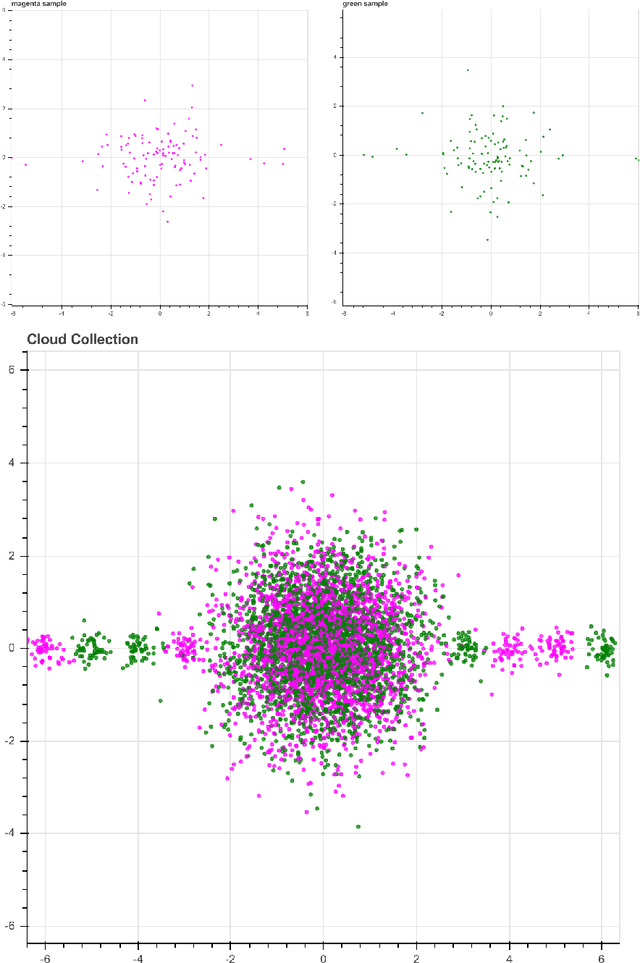
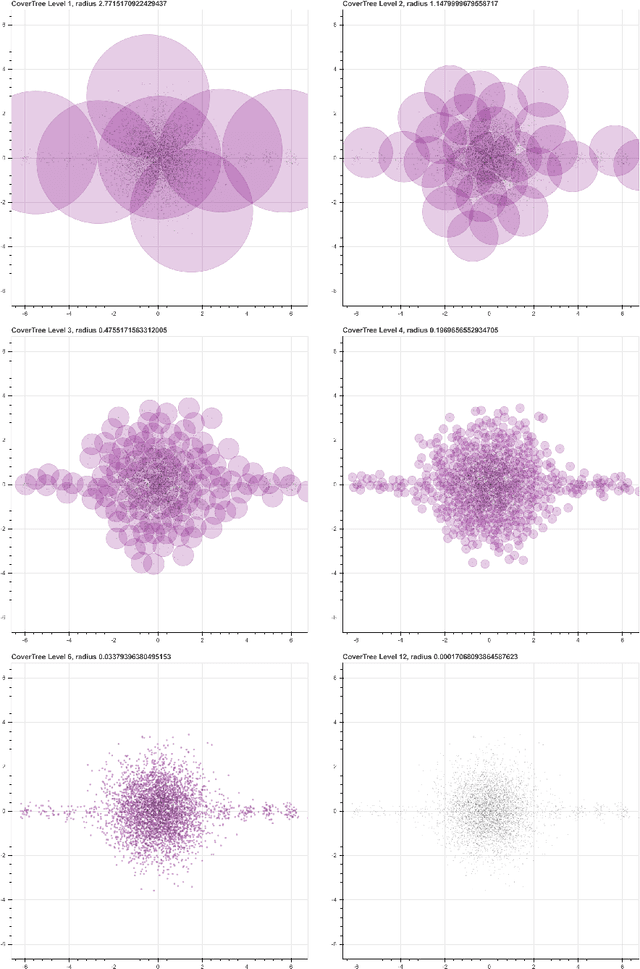
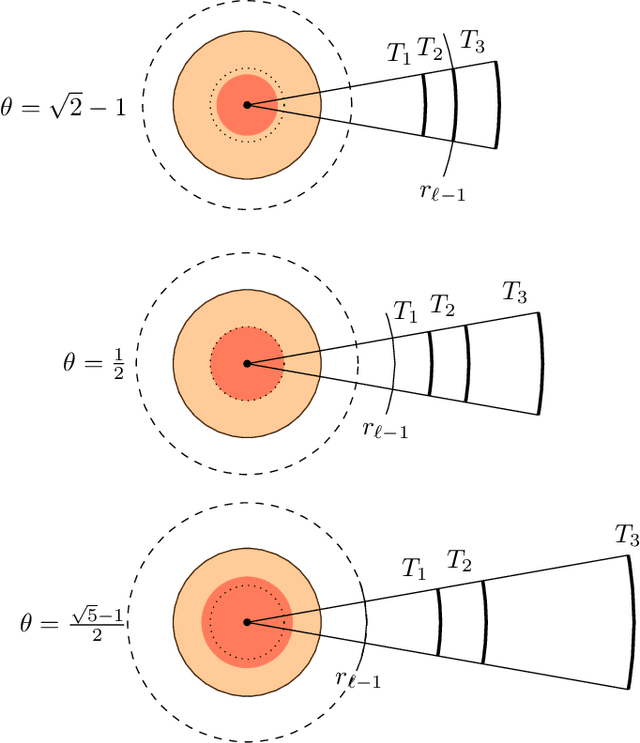
We introduce a new algorithm, called CDER, for supervised machine learning that merges the multi-scale geometric properties of Cover Trees with the information-theoretic properties of entropy. CDER applies to a training set of labeled pointclouds embedded in a common Euclidean space. If typical pointclouds corresponding to distinct labels tend to differ at any scale in any sub-region, CDER can identify these differences in (typically) linear time, creating a set of distributional coordinates which act as a feature extraction mechanism for supervised learning. We describe theoretical properties and implementation details of CDER, and illustrate its benefits on several synthetic examples.

Geometric Cross-Modal Comparison of Heterogeneous Sensor Data

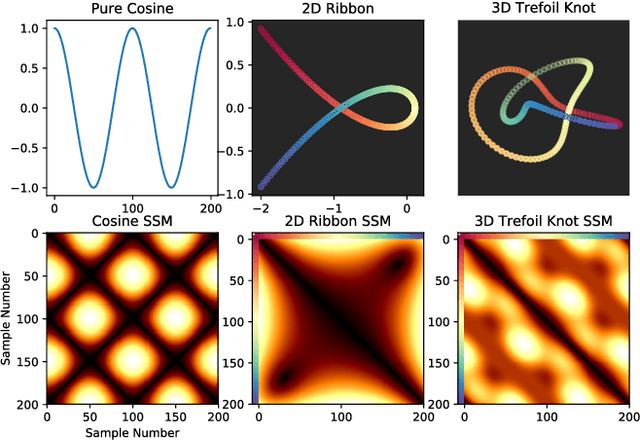
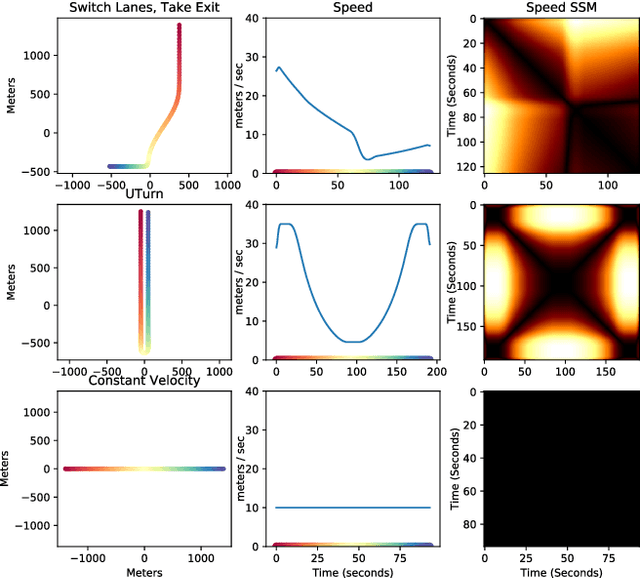
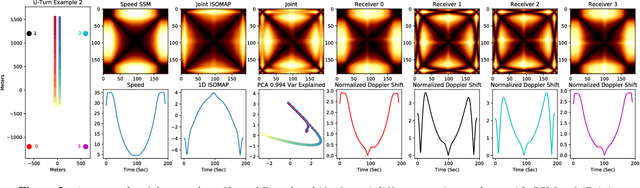
In this work, we address the problem of cross-modal comparison of aerial data streams. A variety of simulated automobile trajectories are sensed using two different modalities: full-motion video, and radio-frequency (RF) signals received by detectors at various locations. The information represented by the two modalities is compared using self-similarity matrices (SSMs) corresponding to time-ordered point clouds in feature spaces of each of these data sources; we note that these feature spaces can be of entirely different scale and dimensionality. Several metrics for comparing SSMs are explored, including a cutting-edge time-warping technique that can simultaneously handle local time warping and partial matches, while also controlling for the change in geometry between feature spaces of the two modalities. We note that this technique is quite general, and does not depend on the choice of modalities. In this particular setting, we demonstrate that the cross-modal distance between SSMs corresponding to the same trajectory type is smaller than the cross-modal distance between SSMs corresponding to distinct trajectory types, and we formalize this observation via precision-recall metrics in experiments. Finally, we comment on promising implications of these ideas for future integration into multiple-hypothesis tracking systems.