Replay Attacks Against Audio Deepfake Detection

We show how replay attacks undermine audio deepfake detection: By playing and re-recording deepfake audio through various speakers and microphones, we make spoofed samples appear authentic to the detection model. To study this phenomenon in more detail, we introduce ReplayDF, a dataset of recordings derived from M-AILABS and MLAAD, featuring 109 speaker-microphone combinations across six languages and four TTS models. It includes diverse acoustic conditions, some highly challenging for detection. Our analysis of six open-source detection models across five datasets reveals significant vulnerability, with the top-performing W2V2-AASIST model's Equal Error Rate (EER) surging from 4.7% to 18.2%. Even with adaptive Room Impulse Response (RIR) retraining, performance remains compromised with an 11.0% EER. We release ReplayDF for non-commercial research use.

Improving Metric Dimensionality Reduction with Distributed Topology

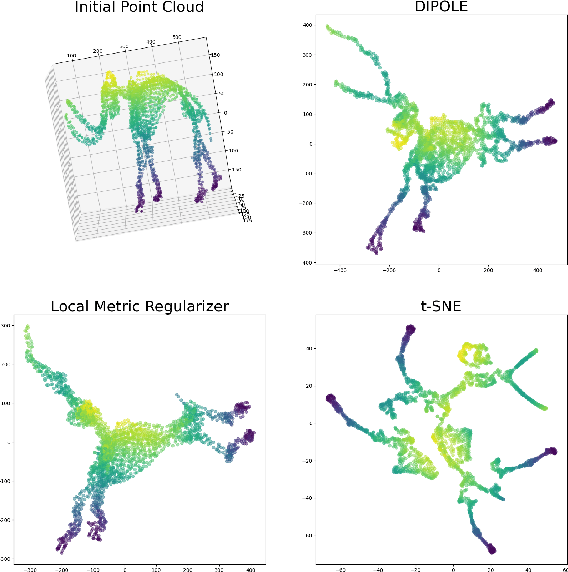
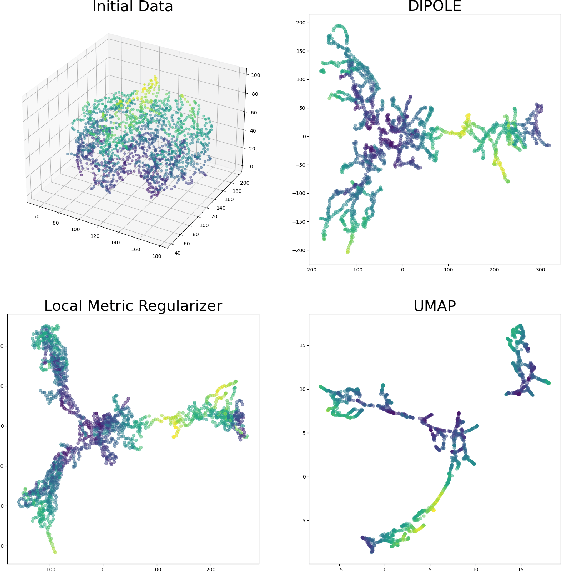
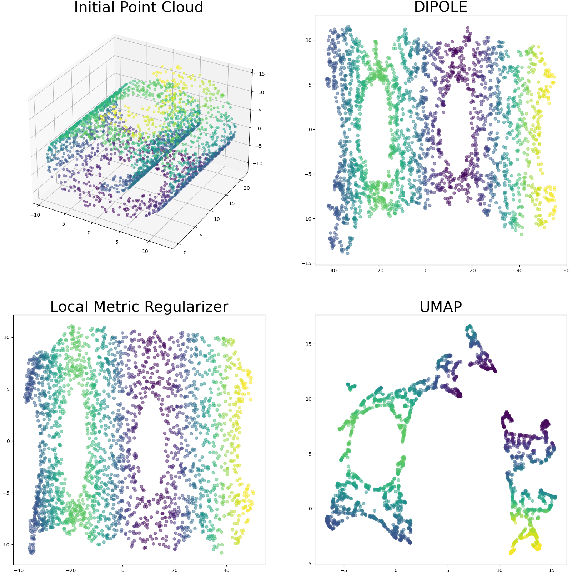
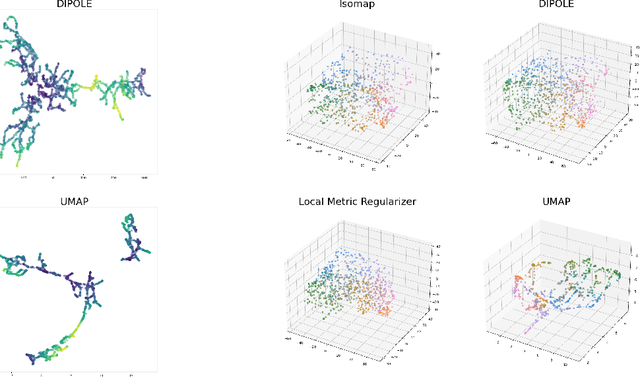
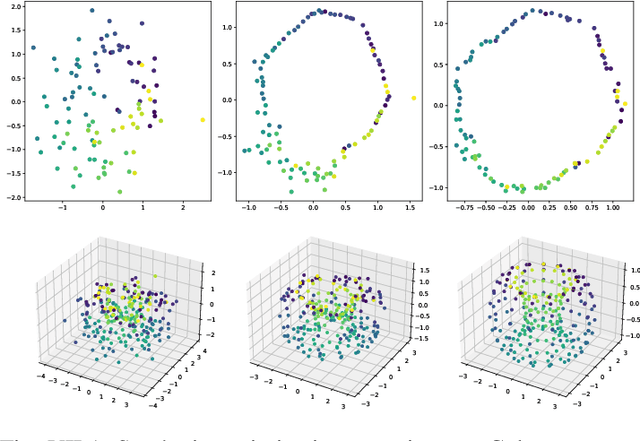
We propose a novel approach to dimensionality reduction combining techniques of metric geometry and distributed persistent homology, in the form of a gradient-descent based method called DIPOLE. DIPOLE is a dimensionality-reduction post-processing step that corrects an initial embedding by minimizing a loss functional with both a local, metric term and a global, topological term. By fixing an initial embedding method (we use Isomap), DIPOLE can also be viewed as a full dimensionality-reduction pipeline. This framework is based on the strong theoretical and computational properties of distributed persistent homology and comes with the guarantee of almost sure convergence. We observe that DIPOLE outperforms popular methods like UMAP, t-SNE, and Isomap on a number of popular datasets, both visually and in terms of precise quantitative metrics.

From Geometry to Topology: Inverse Theorems for Distributed Persistence

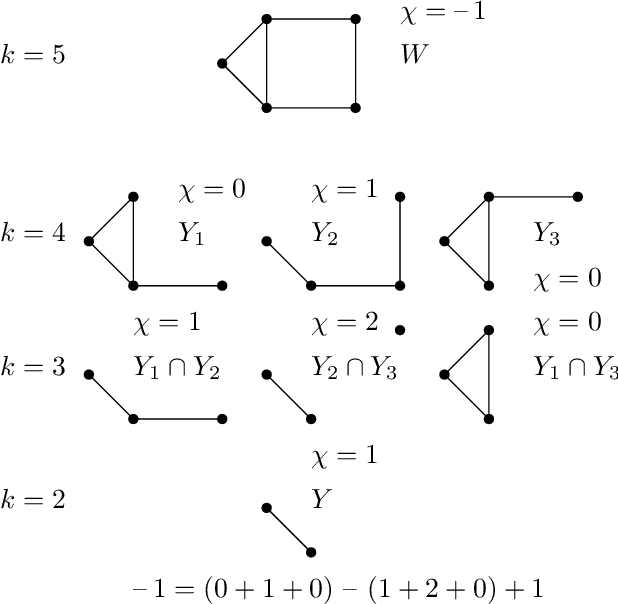
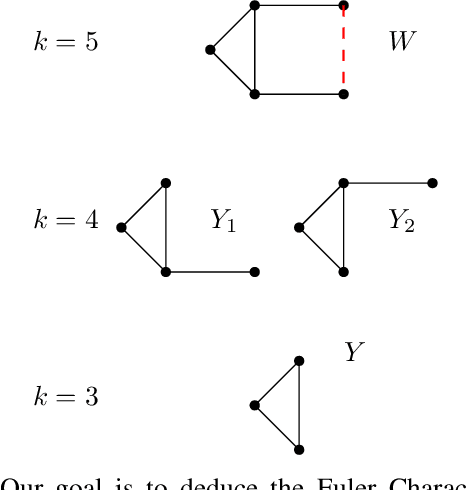
What is the "right" topological invariant of a large point cloud X? Prior research has focused on estimating the full persistence diagram of X, a quantity that is very expensive to compute, unstable to outliers, and far from a sufficient statistic. We therefore propose that the correct invariant is not the persistence diagram of X, but rather the collection of persistence diagrams of many small subsets. This invariant, which we call "distributed persistence," is trivially parallelizable, more stable to outliers, and has a rich inverse theory. The map from the space of point clouds (with the quasi-isometry metric) to the space of distributed persistence invariants (with the Hausdorff-Bottleneck distance) is a global quasi-isometry. This is a much stronger property than simply being injective, as it implies that the inverse of a small neighborhood is a small neighborhood, and is to our knowledge the only result of its kind in the TDA literature. Moreover, the quasi-isometry bounds depend on the size of the subsets taken, so that as the size of these subsets goes from small to large, the invariant interpolates between a purely geometric one and a topological one. Lastly, we note that our inverse results do not actually require considering all subsets of a fixed size (an enormous collection), but a relatively small collection satisfying certain covering properties that arise with high probability when randomly sampling subsets. These theoretical results are complemented by two synthetic experiments demonstrating the use of distributed persistence in practice.

A Fast and Robust Method for Global Topological Functional Optimization

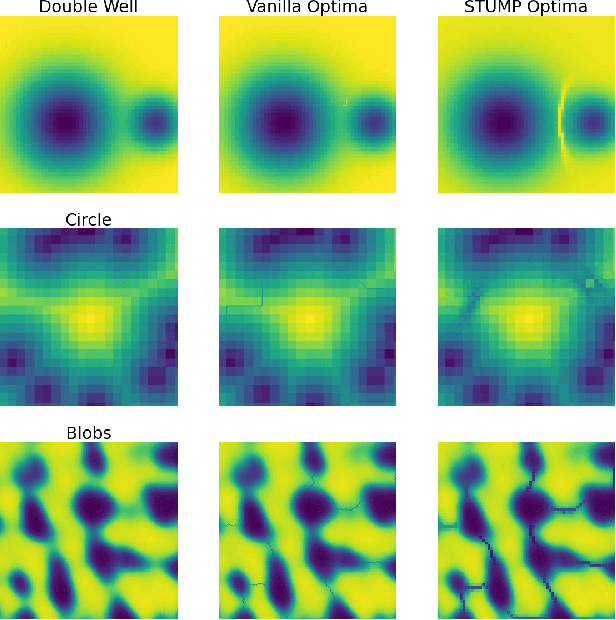
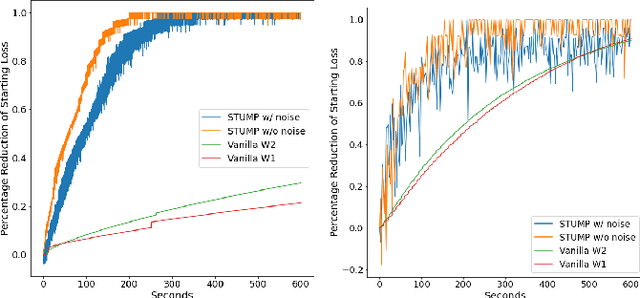
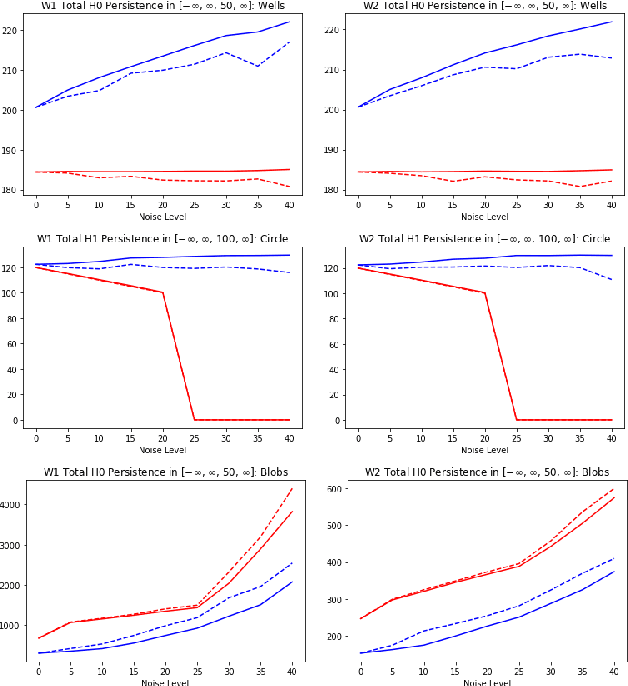
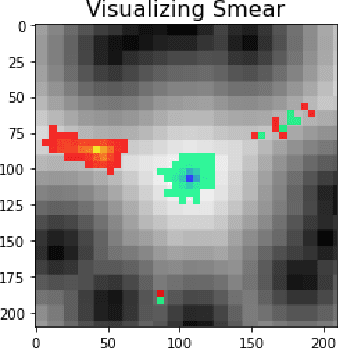
Topological statistics, in the form of persistence diagrams, are a class of shape descriptors that capture global structural information in data. The mapping from data structures to persistence diagrams is almost everywhere differentiable, allowing for topological gradients to be backpropagated to ordinary gradients. However, as a method for optimizing a topological functional, this backpropagation method is expensive, unstable, and produces very fragile optima. Our contribution is to introduce a novel backpropagation scheme that is significantly faster, more stable, and produces more robust optima. Moreover, this scheme can also be used to produce a stable visualization of dots in a persistence diagram as a distribution over critical, and near-critical, simplices in the data structure.

Nonembeddability of Persistence Diagrams with $p>2$ Wasserstein Metric

Persistence diagrams do not admit an inner product structure compatible with any Wasserstein metric. Hence, when applying kernel methods to persistence diagrams, the underlying feature map necessarily causes distortion. We prove persistence diagrams with the p-Wasserstein metric do not admit a coarse embedding into a Hilbert space when p > 2.

Embeddings of Persistence Diagrams into Hilbert Spaces

Since persistence diagrams do not admit an inner product structure, a map into a Hilbert space is needed in order to use kernel methods. It is natural to ask if such maps necessarily distort the metric on persistence diagrams. We show that persistence diagrams with the bottleneck distance do not even admit a coarse embedding into a Hilbert space. As part of our proof, we show that any separable, bounded metric space isometrically embeds into the space of persistence diagrams with the bottleneck distance. As corollaries, we obtain the generalized roundness, negative type, and asymptotic dimension of this space.