A Convolutional Persistence Transform

We consider a new topological feauturization of $d$-dimensional images, obtained by convolving images with various filters before computing persistence. Viewing a convolution filter as a motif within an image, the persistence diagram of the resulting convolution describes the way the motif is distributed throughout that image. This pipeline, which we call convolutional persistence, extends the capacity of topology to observe patterns in image data. Indeed, we prove that (generically speaking) for any two images one can find some filter for which they produce different persistence diagrams, so that the collection of all possible convolutional persistence diagrams for a given image is an injective invariant. This is proven by showing convolutional persistence to be a special case of another topological invariant, the Persistent Homology Transform. Other advantages of convolutional persistence are improved stability and robustness to noise, greater flexibility for data-dependent vectorizations, and reduced computational complexity for convolutions with large stride vectors. Additionally, we have a suite of experiments showing that convolutions greatly improve the predictive power of persistence on a host of classification tasks, even if one uses random filters and vectorizes the resulting diagrams by recording only their total persistences.

Improving Metric Dimensionality Reduction with Distributed Topology

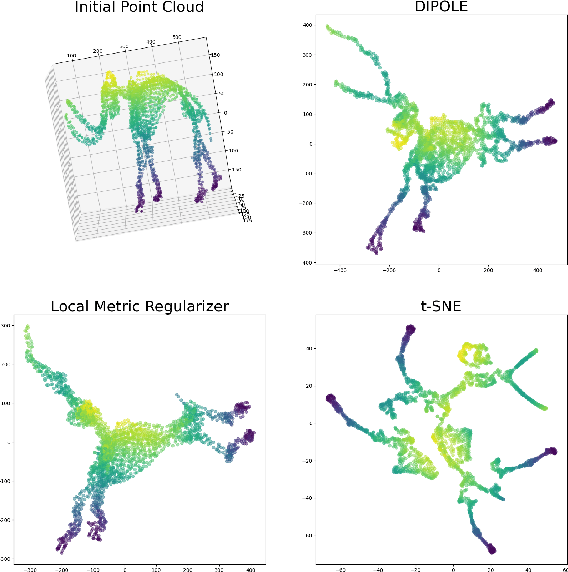
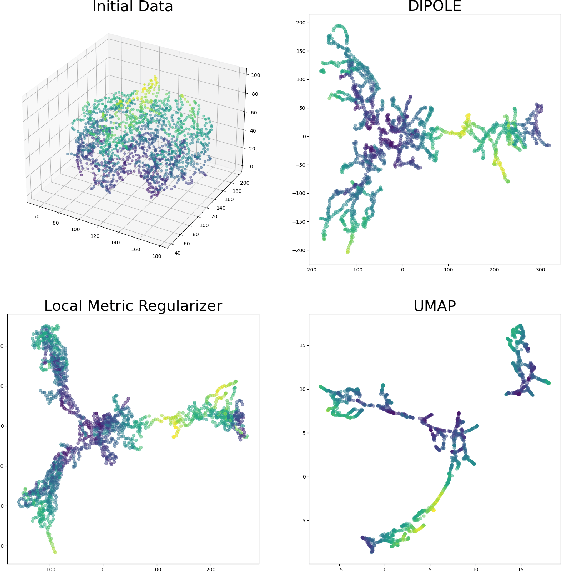
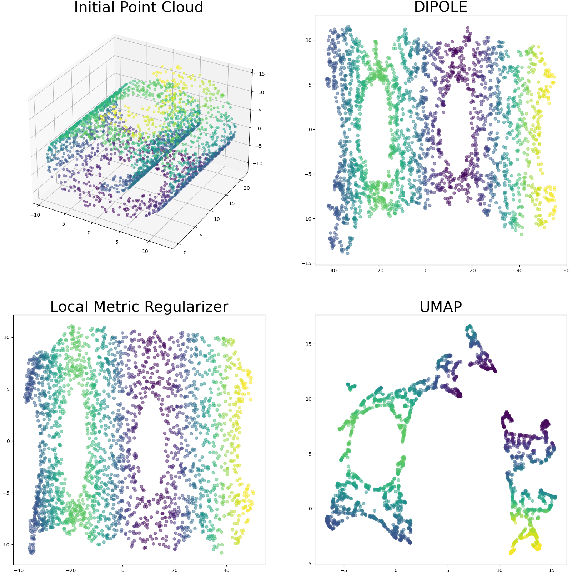
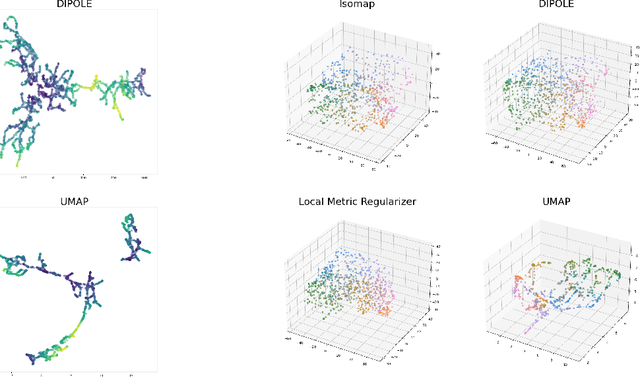
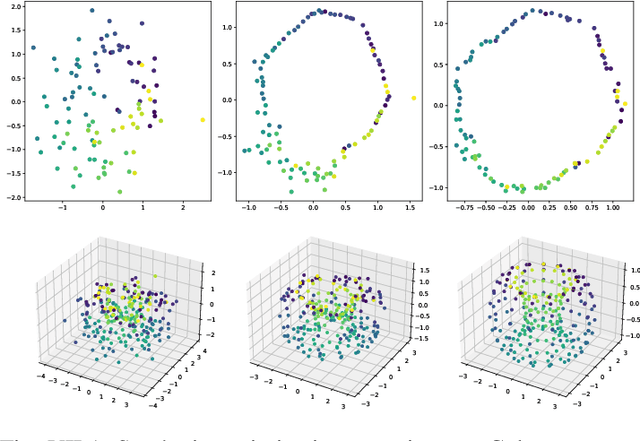
We propose a novel approach to dimensionality reduction combining techniques of metric geometry and distributed persistent homology, in the form of a gradient-descent based method called DIPOLE. DIPOLE is a dimensionality-reduction post-processing step that corrects an initial embedding by minimizing a loss functional with both a local, metric term and a global, topological term. By fixing an initial embedding method (we use Isomap), DIPOLE can also be viewed as a full dimensionality-reduction pipeline. This framework is based on the strong theoretical and computational properties of distributed persistent homology and comes with the guarantee of almost sure convergence. We observe that DIPOLE outperforms popular methods like UMAP, t-SNE, and Isomap on a number of popular datasets, both visually and in terms of precise quantitative metrics.

From Geometry to Topology: Inverse Theorems for Distributed Persistence

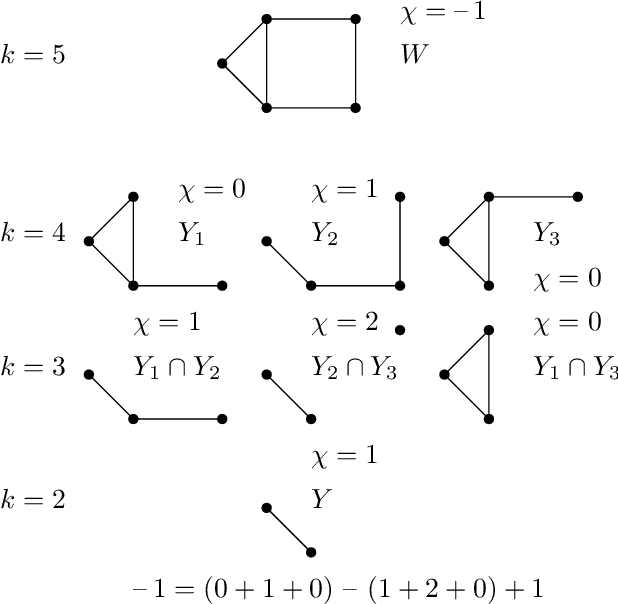
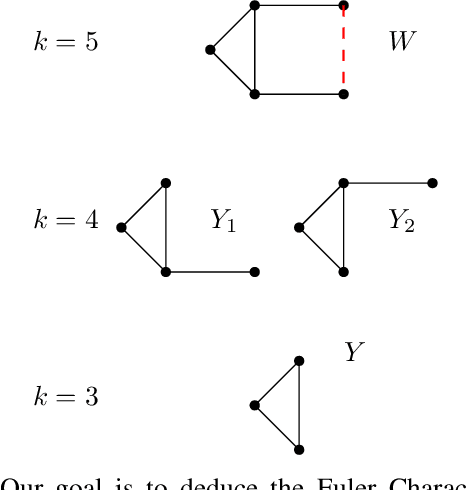
What is the "right" topological invariant of a large point cloud X? Prior research has focused on estimating the full persistence diagram of X, a quantity that is very expensive to compute, unstable to outliers, and far from a sufficient statistic. We therefore propose that the correct invariant is not the persistence diagram of X, but rather the collection of persistence diagrams of many small subsets. This invariant, which we call "distributed persistence," is trivially parallelizable, more stable to outliers, and has a rich inverse theory. The map from the space of point clouds (with the quasi-isometry metric) to the space of distributed persistence invariants (with the Hausdorff-Bottleneck distance) is a global quasi-isometry. This is a much stronger property than simply being injective, as it implies that the inverse of a small neighborhood is a small neighborhood, and is to our knowledge the only result of its kind in the TDA literature. Moreover, the quasi-isometry bounds depend on the size of the subsets taken, so that as the size of these subsets goes from small to large, the invariant interpolates between a purely geometric one and a topological one. Lastly, we note that our inverse results do not actually require considering all subsets of a fixed size (an enormous collection), but a relatively small collection satisfying certain covering properties that arise with high probability when randomly sampling subsets. These theoretical results are complemented by two synthetic experiments demonstrating the use of distributed persistence in practice.

A Fast and Robust Method for Global Topological Functional Optimization

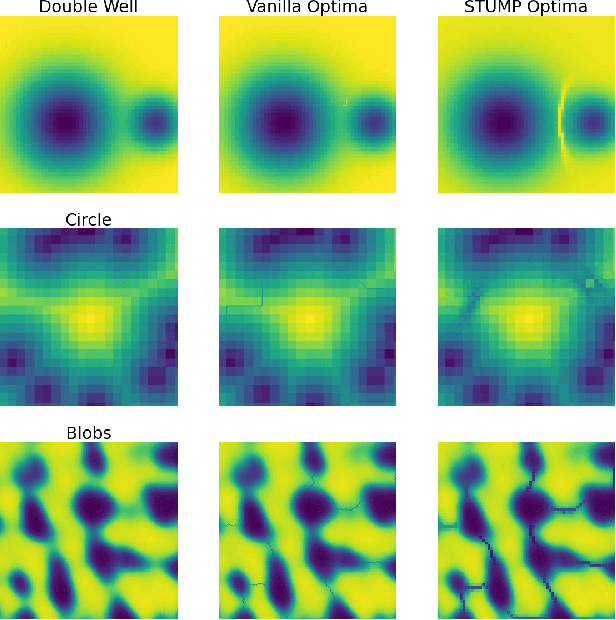
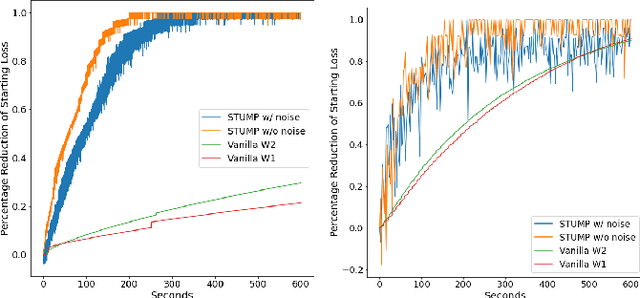
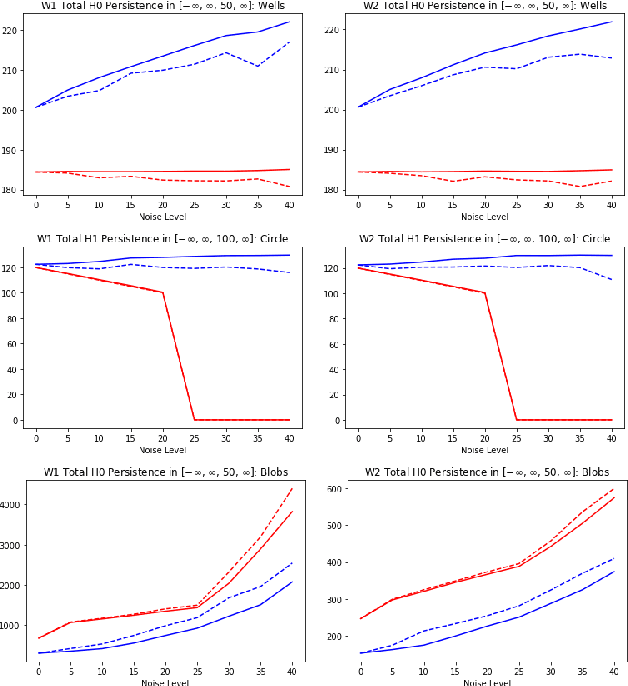
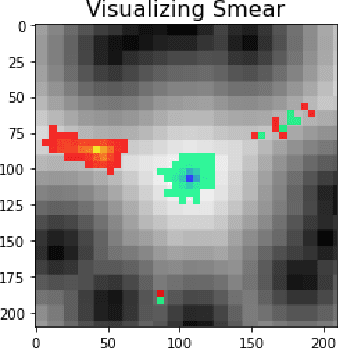
Topological statistics, in the form of persistence diagrams, are a class of shape descriptors that capture global structural information in data. The mapping from data structures to persistence diagrams is almost everywhere differentiable, allowing for topological gradients to be backpropagated to ordinary gradients. However, as a method for optimizing a topological functional, this backpropagation method is expensive, unstable, and produces very fragile optima. Our contribution is to introduce a novel backpropagation scheme that is significantly faster, more stable, and produces more robust optima. Moreover, this scheme can also be used to produce a stable visualization of dots in a persistence diagram as a distribution over critical, and near-critical, simplices in the data structure.

Geometric Fusion via Joint Delay Embeddings

We introduce geometric and topological methods to develop a new framework for fusing multi-sensor time series. This framework consists of two steps: (1) a joint delay embedding, which reconstructs a high-dimensional state space in which our sensors correspond to observation functions, and (2) a simple orthogonalization scheme, which accounts for tangencies between such observation functions, and produces a more diversified geometry on the embedding space. We conclude with some synthetic and real-world experiments demonstrating that our framework outperforms traditional metric fusion methods.