Mixup Barcodes: Quantifying Geometric-Topological Interactions between Point Clouds

We combine standard persistent homology with image persistent homology to define a novel way of characterizing shapes and interactions between them. In particular, we introduce: (1) a mixup barcode, which captures geometric-topological interactions (mixup) between two point sets in arbitrary dimension; (2) simple summary statistics, total mixup and total percentage mixup, which quantify the complexity of the interactions as a single number; (3) a software tool for playing with the above. As a proof of concept, we apply this tool to a problem arising from machine learning. In particular, we study the disentanglement in embeddings of different classes. The results suggest that topological mixup is a useful method for characterizing interactions for low and high-dimensional data. Compared to the typical usage of persistent homology, the new tool is sensitive to the geometric locations of the topological features, which is often desirable.

Activation Landscapes as a Topological Summary of Neural Network Performance

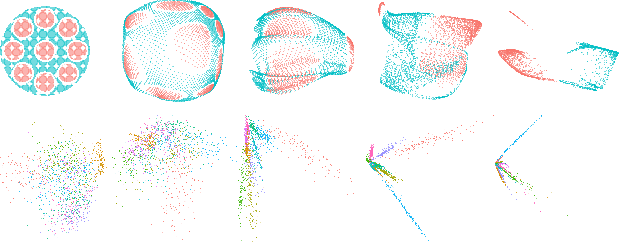
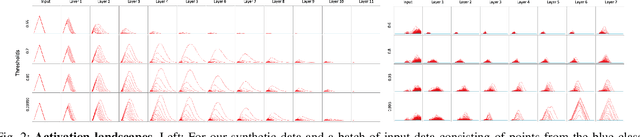
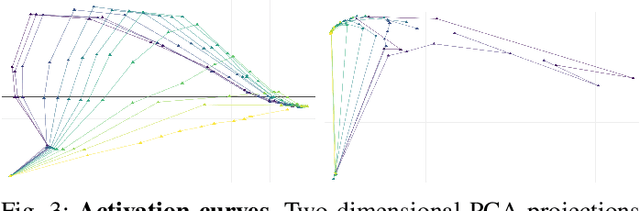
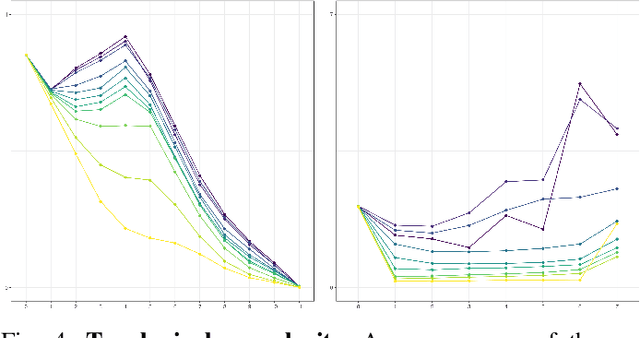
We use topological data analysis (TDA) to study how data transforms as it passes through successive layers of a deep neural network (DNN). We compute the persistent homology of the activation data for each layer of the network and summarize this information using persistence landscapes. The resulting feature map provides both an informative visual- ization of the network and a kernel for statistical analysis and machine learning. We observe that the topological complexity often increases with training and that the topological complexity does not decrease with each layer.

Persistent homology detects curvature

In topological data analysis, persistent homology is used to study the "shape of data". Persistent homology computations are completely characterized by a set of intervals called a bar code. It is often said that the long intervals represent the "topological signal" and the short intervals represent "noise". We give evidence to dispute this thesis, showing that the short intervals encode geometric information. Specifically, we prove that persistent homology detects the curvature of disks from which points have been sampled. We describe a general computational framework for solving inverse problems using the average persistence landscape, a continuous mapping from metric spaces with a probability measure to a Hilbert space. In the present application, the average persistence landscapes of points sampled from disks of constant curvature results in a path in this Hilbert space which may be learned using standard tools from statistical and machine learning.

Embeddings of Persistence Diagrams into Hilbert Spaces

Since persistence diagrams do not admit an inner product structure, a map into a Hilbert space is needed in order to use kernel methods. It is natural to ask if such maps necessarily distort the metric on persistence diagrams. We show that persistence diagrams with the bottleneck distance do not even admit a coarse embedding into a Hilbert space. As part of our proof, we show that any separable, bounded metric space isometrically embeds into the space of persistence diagrams with the bottleneck distance. As corollaries, we obtain the generalized roundness, negative type, and asymptotic dimension of this space.

The persistence landscape and some of its properties

Persistence landscapes map persistence diagrams into a function space, which may often be taken to be a Banach space or even a Hilbert space. In the latter case, it is a feature map and there is an associated kernel. The main advantage of this summary is that it allows one to apply tools from statistics and machine learning. Furthermore, the mapping from persistence diagrams to persistence landscapes is stable and invertible. We introduce a weighted version of the persistence landscape and define a one-parameter family of Poisson-weighted persistence landscape kernels that may be useful for learning. We also demonstrate some additional properties of the persistence landscape. First, the persistence landscape may be viewed as a tropical rational function. Second, in many cases it is possible to exactly reconstruct all of the component persistence diagrams from an average persistence landscape. It follows that the persistence landscape kernel is characteristic for certain generic empirical measures. Finally, the persistence landscape distance may be arbitrarily small compared to the interleaving distance.

Min-type Morse theory for configuration spaces of hard spheres

We study configuration spaces of hard spheres in a bounded region. We develop a general Morse-theoretic framework, and show that mechanically balanced configurations play the role of critical points. As an application, we find the precise threshold radius for a configuration space to be homotopy equivalent to the configuration space of points.