Hubert Wagner
Bregman-Hausdorff divergence: strengthening the connections between computational geometry and machine learning
Apr 09, 2025Abstract:The purpose of this paper is twofold. On a technical side, we propose an extension of the Hausdorff distance from metric spaces to spaces equipped with asymmetric distance measures. Specifically, we focus on the family of Bregman divergences, which includes the popular Kullback--Leibler divergence (also known as relative entropy). As a proof of concept, we use the resulting Bregman--Hausdorff divergence to compare two collections of probabilistic predictions produced by different machine learning models trained using the relative entropy loss. The algorithms we propose are surprisingly efficient even for large inputs with hundreds of dimensions. In addition to the introduction of this technical concept, we provide a survey. It outlines the basics of Bregman geometry, as well as computational geometry algorithms. We focus on algorithms that are compatible with this geometry and are relevant for machine learning.
Mixup Barcodes: Quantifying Geometric-Topological Interactions between Point Clouds
Feb 23, 2024Abstract:We combine standard persistent homology with image persistent homology to define a novel way of characterizing shapes and interactions between them. In particular, we introduce: (1) a mixup barcode, which captures geometric-topological interactions (mixup) between two point sets in arbitrary dimension; (2) simple summary statistics, total mixup and total percentage mixup, which quantify the complexity of the interactions as a single number; (3) a software tool for playing with the above. As a proof of concept, we apply this tool to a problem arising from machine learning. In particular, we study the disentanglement in embeddings of different classes. The results suggest that topological mixup is a useful method for characterizing interactions for low and high-dimensional data. Compared to the typical usage of persistent homology, the new tool is sensitive to the geometric locations of the topological features, which is often desirable.
Topological Detection of Trojaned Neural Networks
Jun 11, 2021
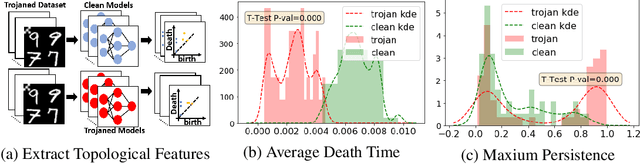

Abstract:Deep neural networks are known to have security issues. One particular threat is the Trojan attack. It occurs when the attackers stealthily manipulate the model's behavior through Trojaned training samples, which can later be exploited. Guided by basic neuroscientific principles we discover subtle -- yet critical -- structural deviation characterizing Trojaned models. In our analysis we use topological tools. They allow us to model high-order dependencies in the networks, robustly compare different networks, and localize structural abnormalities. One interesting observation is that Trojaned models develop short-cuts from input to output layers. Inspired by these observations, we devise a strategy for robust detection of Trojaned models. Compared to standard baselines it displays better performance on multiple benchmarks.
Streaming Algorithm for Euler Characteristic Curves of Multidimensional Images
Oct 17, 2018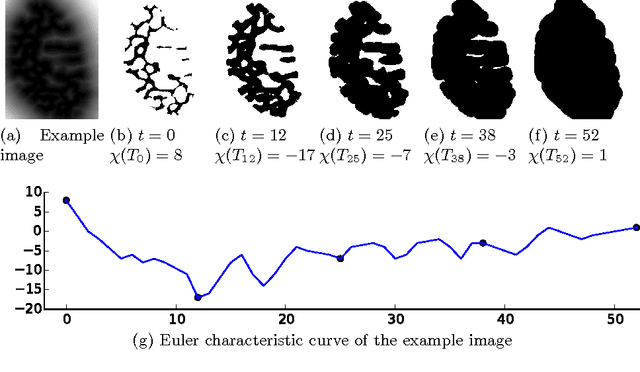
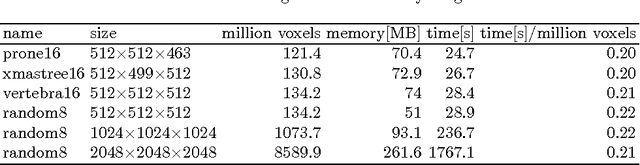
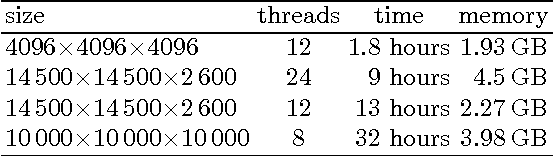
Abstract:We present an efficient algorithm to compute Euler characteristic curves of gray scale images of arbitrary dimension. In various applications the Euler characteristic curve is used as a descriptor of an image. Our algorithm is the first streaming algorithm for Euler characteristic curves. The usage of streaming removes the necessity to store the entire image in RAM. Experiments show that our implementation handles terabyte scale images on commodity hardware. Due to lock-free parallelism, it scales well with the number of processor cores. Our software---CHUNKYEuler---is available as open source on Bitbucket. Additionally, we put the concept of the Euler characteristic curve in the wider context of computational topology. In particular, we explain the connection with persistence diagrams.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge