The Impact of Changes in Resolution on the Persistent Homology of Images

Digital images enable quantitative analysis of material properties at micro and macro length scales, but choosing an appropriate resolution when acquiring the image is challenging. A high resolution means longer image acquisition and larger data requirements for a given sample, but if the resolution is too low, significant information may be lost. This paper studies the impact of changes in resolution on persistent homology, a tool from topological data analysis that provides a signature of structure in an image across all length scales. Given prior information about a function, the geometry of an object, or its density distribution at a given resolution, we provide methods to select the coarsest resolution yielding results within an acceptable tolerance. We present numerical case studies for an illustrative synthetic example and samples from porous materials where the theoretical bounds are unknown.

Duality in Persistent Homology of Images

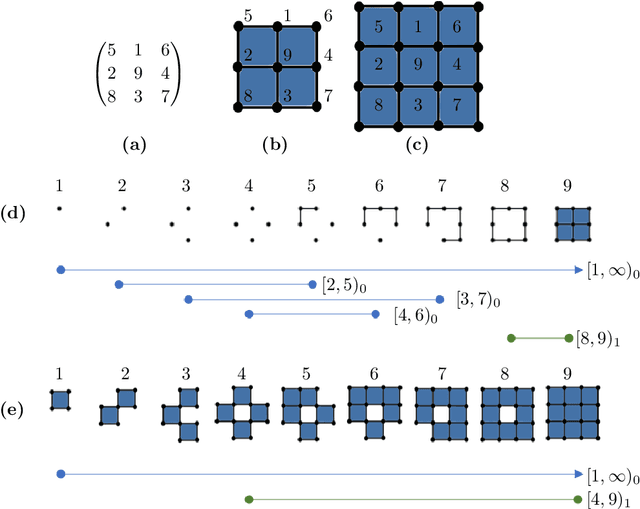
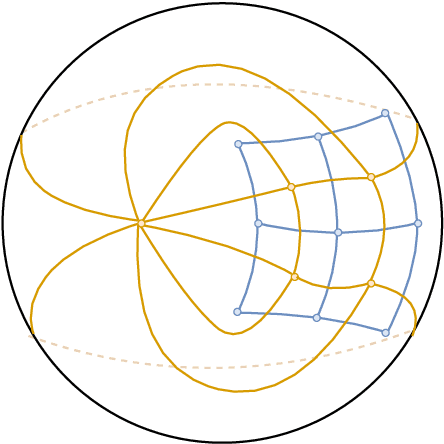
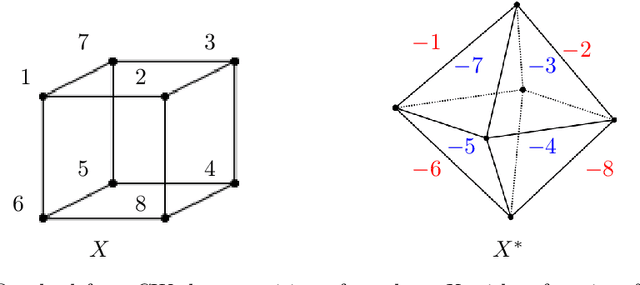
We derive the relationship between the persistent homology barcodes of two dual filtered CW complexes. Applied to greyscale digital images, we obtain an algorithm to convert barcodes between the two different (dual) topological models of pixel connectivity.

Streaming Algorithm for Euler Characteristic Curves of Multidimensional Images

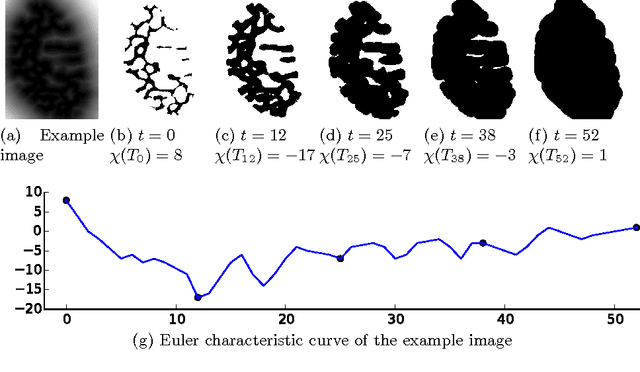
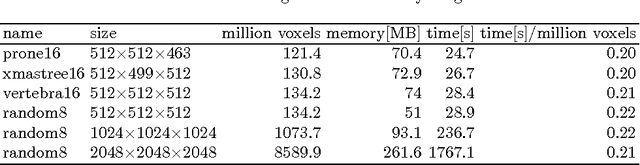
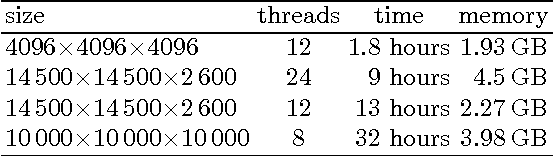
We present an efficient algorithm to compute Euler characteristic curves of gray scale images of arbitrary dimension. In various applications the Euler characteristic curve is used as a descriptor of an image. Our algorithm is the first streaming algorithm for Euler characteristic curves. The usage of streaming removes the necessity to store the entire image in RAM. Experiments show that our implementation handles terabyte scale images on commodity hardware. Due to lock-free parallelism, it scales well with the number of processor cores. Our software---CHUNKYEuler---is available as open source on Bitbucket. Additionally, we put the concept of the Euler characteristic curve in the wider context of computational topology. In particular, we explain the connection with persistence diagrams.