Brittany Story
A Topological Deep Learning Framework for Neural Spike Decoding
Dec 01, 2022Abstract:The brain's spatial orientation system uses different neuron ensembles to aid in environment-based navigation. One of the ways brains encode spatial information is through grid cells, layers of decked neurons that overlay to provide environment-based navigation. These neurons fire in ensembles where several neurons fire at once to activate a single grid. We want to capture this firing structure and use it to decode grid cell data. Understanding, representing, and decoding these neural structures require models that encompass higher order connectivity than traditional graph-based models may provide. To that end, in this work, we develop a topological deep learning framework for neural spike train decoding. Our framework combines unsupervised simplicial complex discovery with the power of deep learning via a new architecture we develop herein called a simplicial convolutional recurrent neural network (SCRNN). Simplicial complexes, topological spaces that use not only vertices and edges but also higher-dimensional objects, naturally generalize graphs and capture more than just pairwise relationships. Additionally, this approach does not require prior knowledge of the neural activity beyond spike counts, which removes the need for similarity measurements. The effectiveness and versatility of the SCRNN is demonstrated on head direction data to test its performance and then applied to grid cell datasets with the task to automatically predict trajectories.
The Impact of Changes in Resolution on the Persistent Homology of Images
Nov 10, 2021
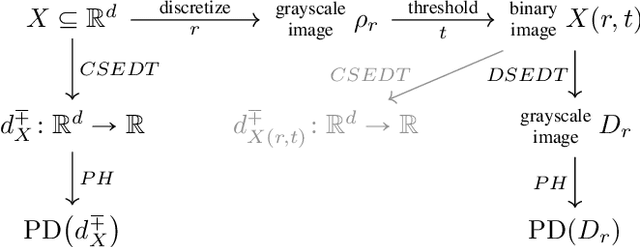
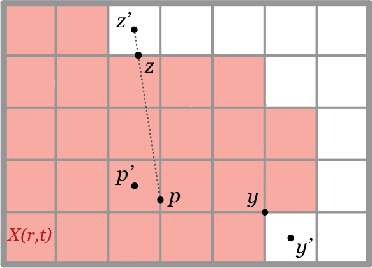
Abstract:Digital images enable quantitative analysis of material properties at micro and macro length scales, but choosing an appropriate resolution when acquiring the image is challenging. A high resolution means longer image acquisition and larger data requirements for a given sample, but if the resolution is too low, significant information may be lost. This paper studies the impact of changes in resolution on persistent homology, a tool from topological data analysis that provides a signature of structure in an image across all length scales. Given prior information about a function, the geometry of an object, or its density distribution at a given resolution, we provide methods to select the coarsest resolution yielding results within an acceptable tolerance. We present numerical case studies for an illustrative synthetic example and samples from porous materials where the theoretical bounds are unknown.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge