The Impact of Changes in Resolution on the Persistent Homology of Images

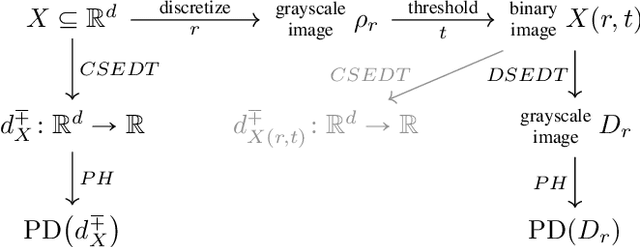
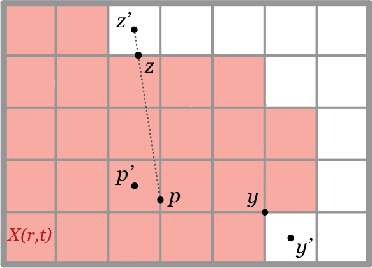
Digital images enable quantitative analysis of material properties at micro and macro length scales, but choosing an appropriate resolution when acquiring the image is challenging. A high resolution means longer image acquisition and larger data requirements for a given sample, but if the resolution is too low, significant information may be lost. This paper studies the impact of changes in resolution on persistent homology, a tool from topological data analysis that provides a signature of structure in an image across all length scales. Given prior information about a function, the geometry of an object, or its density distribution at a given resolution, we provide methods to select the coarsest resolution yielding results within an acceptable tolerance. We present numerical case studies for an illustrative synthetic example and samples from porous materials where the theoretical bounds are unknown.

Localized Persistent Homologies for more Effective Deep Learning

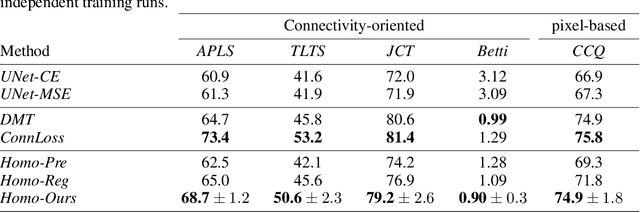
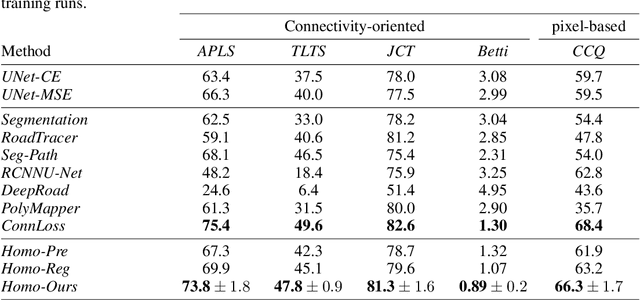
Persistent Homologies have been successfully used to increase the performance of deep networks trained to detect curvilinear structures and to improve the topological quality of the results. However, existing methods are very global and ignore the location of topological features. In this paper, we introduce an approach that relies on a new filtration function to account for location during network training. We demonstrate experimentally on 2D images of roads and 3D image stacks of neuronal processes that networks trained in this manner are better at recovering the topology of the curvilinear structures they extract.

Duality in Persistent Homology of Images

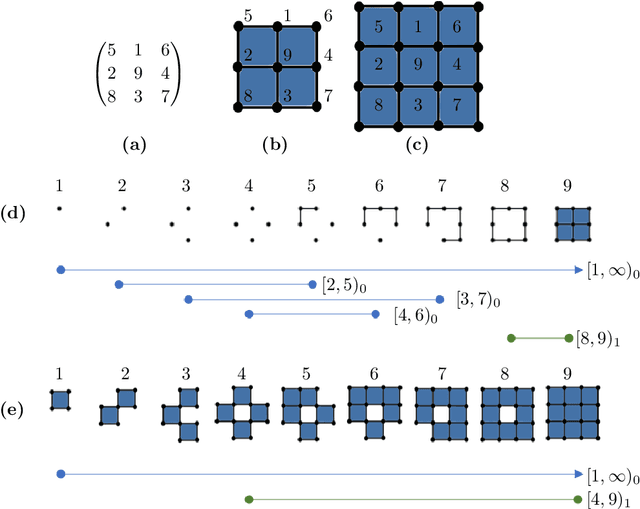
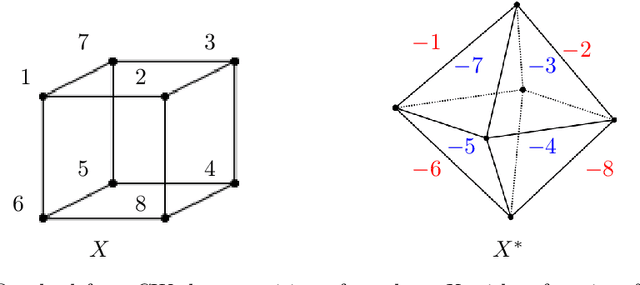
We derive the relationship between the persistent homology barcodes of two dual filtered CW complexes. Applied to greyscale digital images, we obtain an algorithm to convert barcodes between the two different (dual) topological models of pixel connectivity.

A Topological "Reading" Lesson: Classification of MNIST using TDA

We present a way to use Topological Data Analysis (TDA) for machine learning tasks on grayscale images. We apply persistent homology to generate a wide range of topological features using a point cloud obtained from an image, its natural grayscale filtration, and different filtrations defined on the binarized image. We show that this topological machine learning pipeline can be used as a highly relevant dimensionality reduction by applying it to the MNIST digits dataset. We conduct a feature selection and study their correlations while providing an intuitive interpretation of their importance, which is relevant in both machine learning and TDA. Finally, we show that we can classify digit images while reducing the size of the feature set by a factor 5 compared to the grayscale pixel value features and maintain similar accuracy.