Doruk Oner
CAPE: Connectivity-Aware Path Enforcement Loss for Curvilinear Structure Delineation
Apr 01, 2025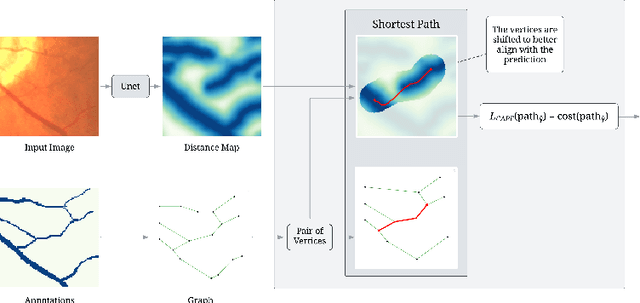
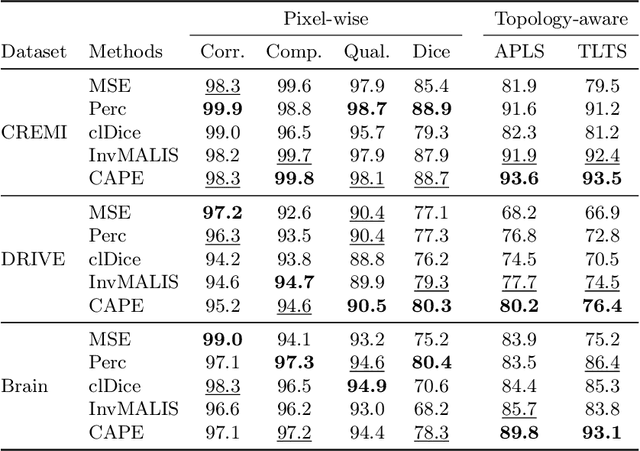
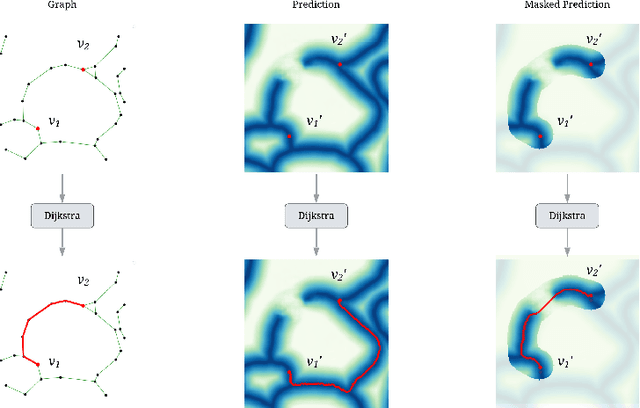
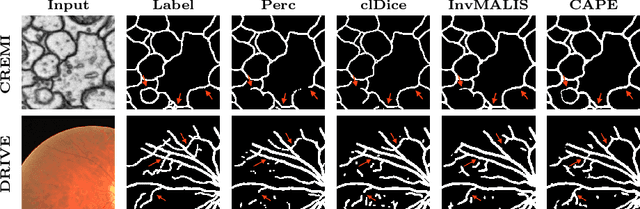
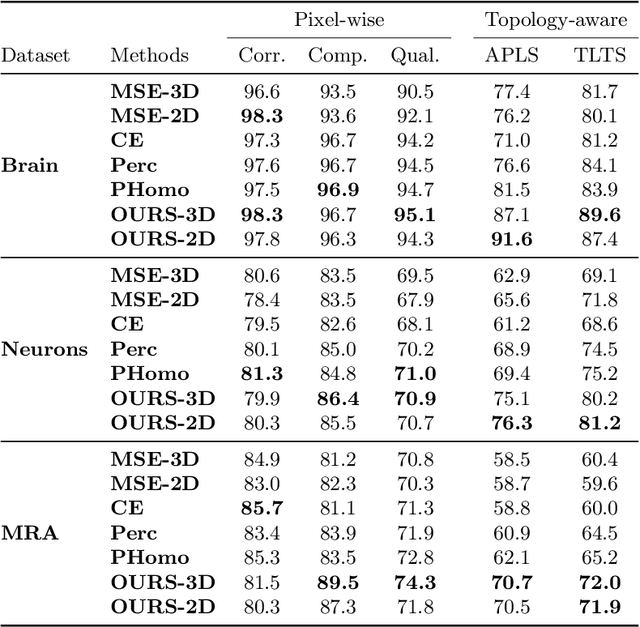
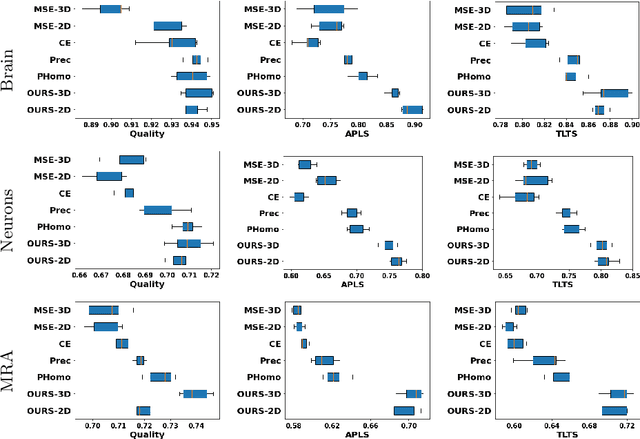
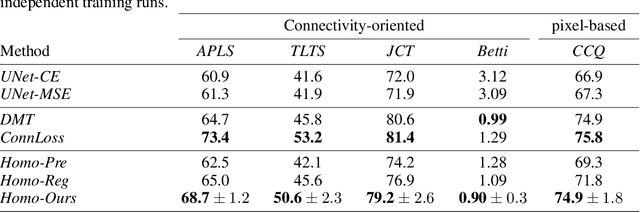
Abstract:Promoting the connectivity of curvilinear structures, such as neuronal processes in biomedical scans and blood vessels in CT images, remains a key challenge in semantic segmentation. Traditional pixel-wise loss functions, including cross-entropy and Dice losses, often fail to capture high-level topological connectivity, resulting in topological mistakes in graphs obtained from prediction maps. In this paper, we propose CAPE (Connectivity-Aware Path Enforcement), a novel loss function designed to enforce connectivity in graphs obtained from segmentation maps by optimizing a graph connectivity metric. CAPE uses the graph representation of the ground truth to select node pairs and determine their corresponding paths within the predicted segmentation through a shortest-path algorithm. Using this, we penalize both disconnections and false positive connections, effectively promoting the model to preserve topological correctness. Experiments on 2D and 3D datasets, including neuron and blood vessel tracing demonstrate that CAPE significantly improves topology-aware metrics and outperforms state-of-the-art methods.
PartSDF: Part-Based Implicit Neural Representation for Composite 3D Shape Parametrization and Optimization
Feb 18, 2025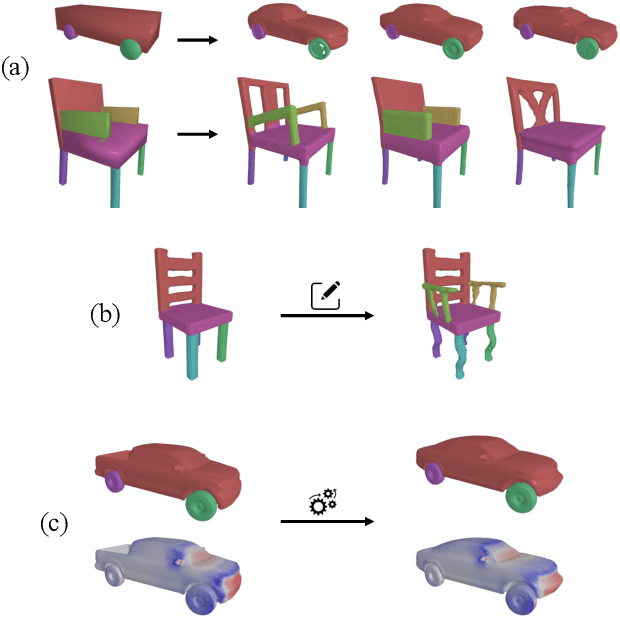
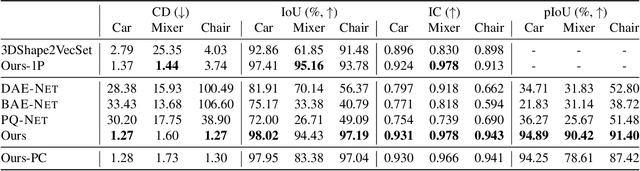
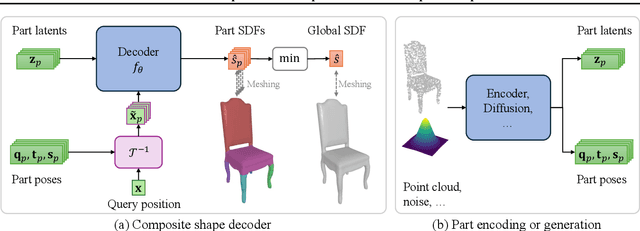
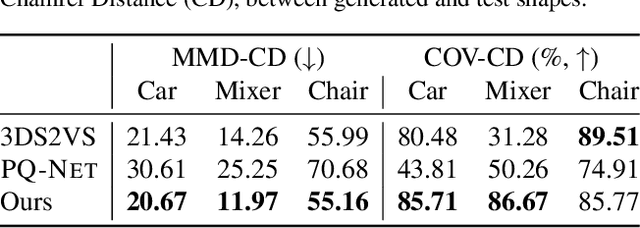
Abstract:Accurate 3D shape representation is essential in engineering applications such as design, optimization, and simulation. In practice, engineering workflows require structured, part-aware representations, as objects are inherently designed as assemblies of distinct components. However, most existing methods either model shapes holistically or decompose them without predefined part structures, limiting their applicability in real-world design tasks. We propose PartSDF, a supervised implicit representation framework that explicitly models composite shapes with independent, controllable parts while maintaining shape consistency. Despite its simple single-decoder architecture, PartSDF outperforms both supervised and unsupervised baselines in reconstruction and generation tasks. We further demonstrate its effectiveness as a structured shape prior for engineering applications, enabling precise control over individual components while preserving overall coherence. Code available at https://github.com/cvlab-epfl/PartSDF.
IT$^3$: Idempotent Test-Time Training
Oct 05, 2024



Abstract:This paper introduces Idempotent Test-Time Training (IT$^3$), a novel approach to addressing the challenge of distribution shift. While supervised-learning methods assume matching train and test distributions, this is rarely the case for machine learning systems deployed in the real world. Test-Time Training (TTT) approaches address this by adapting models during inference, but they are limited by a domain specific auxiliary task. IT$^3$ is based on the universal property of idempotence. An idempotent operator is one that can be applied sequentially without changing the result beyond the initial application, that is $f(f(x))=f(x)$. At training, the model receives an input $x$ along with another signal that can either be the ground truth label $y$ or a neutral "don't know" signal $0$. At test time, the additional signal can only be $0$. When sequentially applying the model, first predicting $y_0 = f(x, 0)$ and then $y_1 = f(x, y_0)$, the distance between $y_0$ and $y_1$ measures certainty and indicates out-of-distribution input $x$ if high. We use this distance, that can be expressed as $||f(x, f(x, 0)) - f(x, 0)||$ as our TTT loss during inference. By carefully optimizing this objective, we effectively train $f(x,\cdot)$ to be idempotent, projecting the internal representation of the input onto the training distribution. We demonstrate the versatility of our approach across various tasks, including corrupted image classification, aerodynamic predictions, tabular data with missing information, age prediction from face, and large-scale aerial photo segmentation. Moreover, these tasks span different architectures such as MLPs, CNNs, and GNNs.
Vision-Based Power Line Cables and Pylons Detection for Low Flying Aircrafts
Jul 19, 2024



Abstract:Power lines are dangerous for low-flying aircrafts, especially in low-visibility conditions. Thus, a vision-based system able to analyze the aircraft's surroundings and to provide the pilots with a "second pair of eyes" can contribute to enhancing their safety. To this end, we have developed a deep learning approach to jointly detect power line cables and pylons from images captured at distances of several hundred meters by aircraft-mounted cameras. In doing so, we have combined a modern convolutional architecture with transfer learning and a loss function adapted to curvilinear structure delineation. We use a single network for both detection tasks and demonstrated its performance on two benchmarking datasets. We have integrated it within an onboard system and run it in flight, and have demonstrated with our experiments that it outperforms the prior distant cable detection method on both datasets, while also successfully detecting pylons, given their annotations are available for the data.
Enabling Uncertainty Estimation in Iterative Neural Networks
Mar 25, 2024Abstract:Turning pass-through network architectures into iterative ones, which use their own output as input, is a well-known approach for boosting performance. In this paper, we argue that such architectures offer an additional benefit: The convergence rate of their successive outputs is highly correlated with the accuracy of the value to which they converge. Thus, we can use the convergence rate as a useful proxy for uncertainty. This results in an approach to uncertainty estimation that provides state-of-the-art estimates at a much lower computational cost than techniques like Ensembles, and without requiring any modifications to the original iterative model. We demonstrate its practical value by embedding it in two application domains: road detection in aerial images and the estimation of aerodynamic properties of 2D and 3D shapes.
Enforcing connectivity of 3D linear structures using their 2D projections
Jul 14, 2022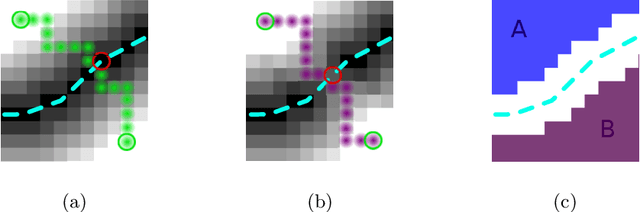
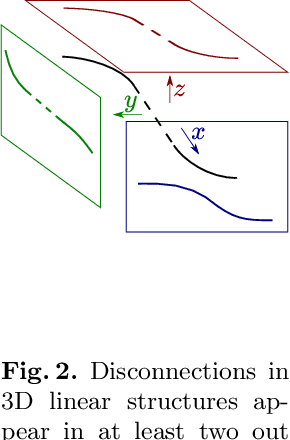
Abstract:Many biological and medical tasks require the delineation of 3D curvilinear structures such as blood vessels and neurites from image volumes. This is typically done using neural networks trained by minimizing voxel-wise loss functions that do not capture the topological properties of these structures. As a result, the connectivity of the recovered structures is often wrong, which lessens their usefulness. In this paper, we propose to improve the 3D connectivity of our results by minimizing a sum of topology-aware losses on their 2D projections. This suffices to increase the accuracy and to reduce the annotation effort required to provide the required annotated training data.
Adjusting the Ground Truth Annotations for Connectivity-Based Learning to Delineate
Dec 06, 2021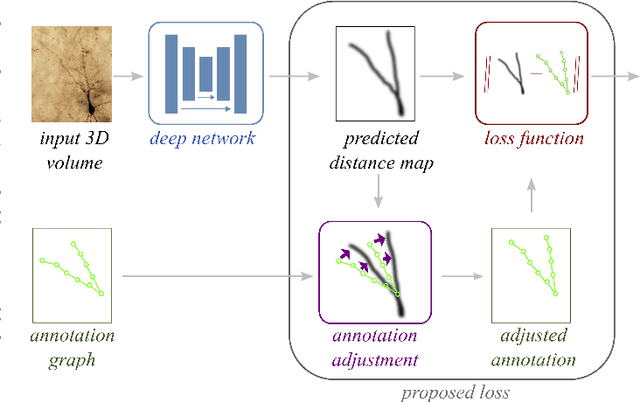
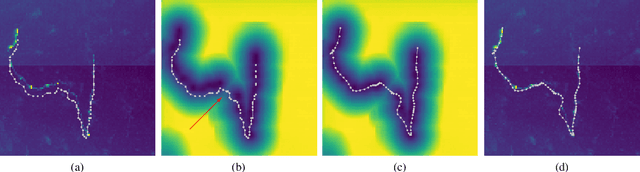
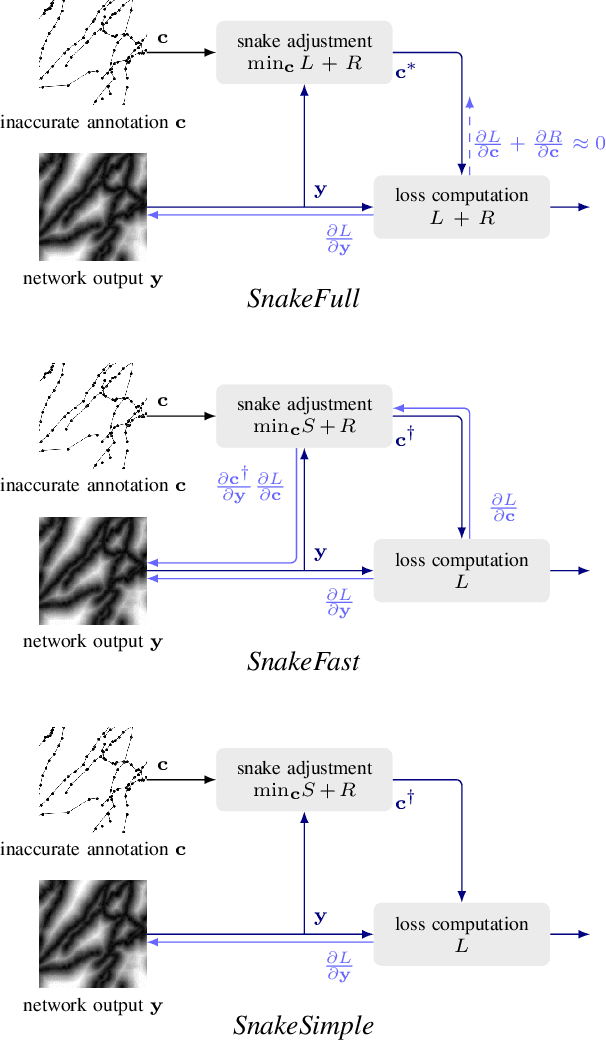

Abstract:Deep learning-based approaches to delineating 3D structure depend on accurate annotations to train the networks. Yet, in practice, people, no matter how conscientious, have trouble precisely delineating in 3D and on a large scale, in part because the data is often hard to interpret visually and in part because the 3D interfaces are awkward to use. In this paper, we introduce a method that explicitly accounts for annotation inaccuracies. To this end, we treat the annotations as active contour models that can deform themselves while preserving their topology. This enables us to jointly train the network and correct potential errors in the original annotations. The result is an approach that boosts performance of deep networks trained with potentially inaccurate annotations.
Localized Persistent Homologies for more Effective Deep Learning
Oct 12, 2021

Abstract:Persistent Homologies have been successfully used to increase the performance of deep networks trained to detect curvilinear structures and to improve the topological quality of the results. However, existing methods are very global and ignore the location of topological features. In this paper, we introduce an approach that relies on a new filtration function to account for location during network training. We demonstrate experimentally on 2D images of roads and 3D image stacks of neuronal processes that networks trained in this manner are better at recovering the topology of the curvilinear structures they extract.
Promoting Connectivity of Network-Like Structures by Enforcing Region Separation
Sep 15, 2020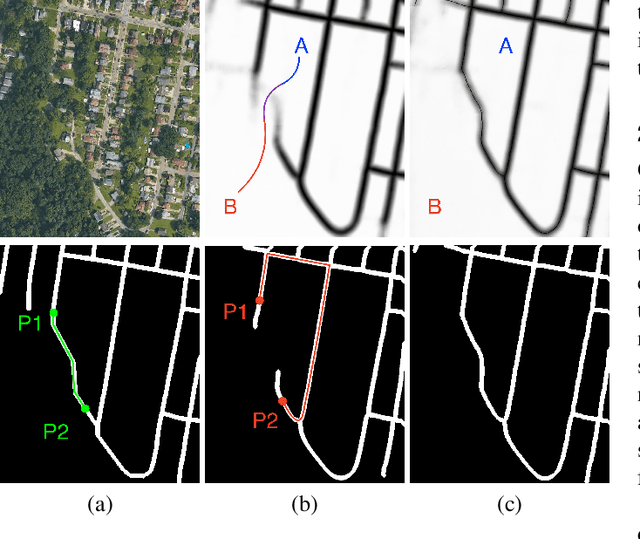
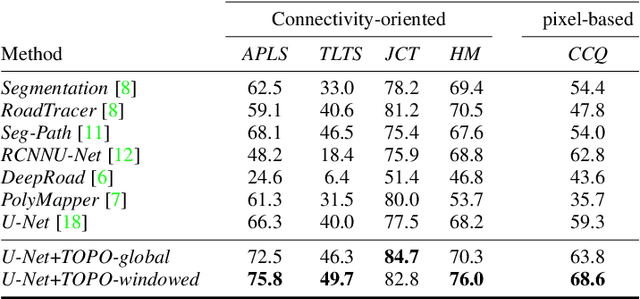
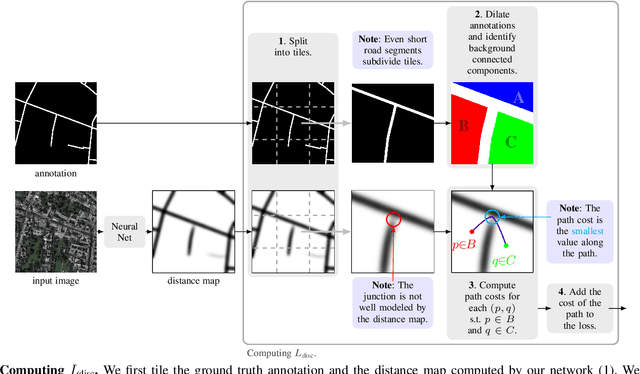
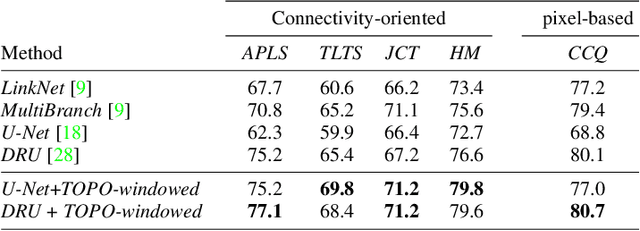
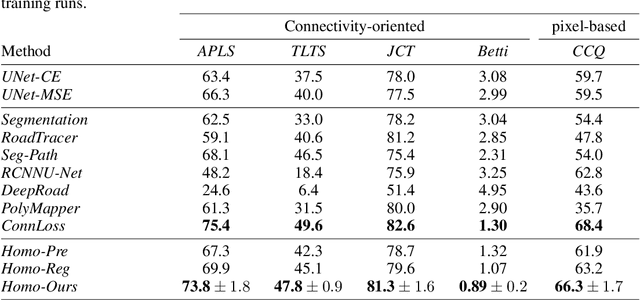
Abstract:We propose a novel, connectivity-oriented loss function for training deep convolutional networks to reconstruct network-like structures, like roads and irrigation canals, from aerial images. The main idea behind our loss is to express the connectivity of roads, or canals, in terms of disconnections that they create between background regions of the image. In simple terms, a gap in the predicted road causes two background regions, that lie on the opposite sides of a ground truth road, to touch in prediction. Our loss function is designed to prevent such unwanted connections between background regions, and therefore close the gaps in predicted roads. It also prevents predicting false positive roads and canals by penalizing unwarranted disconnections of background regions. In order to capture even short, dead-ending road segments, we evaluate the loss in small image crops. We show, in experiments on two standard road benchmarks and a new data set of irrigation canals, that convnets trained with our loss function recover road connectivity so well, that it suffices to skeletonize their output to produce state of the art maps. A distinct advantage of our approach is that the loss can be plugged in to any existing training setup without further modifications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge