Enabling Uncertainty Estimation in Iterative Neural Networks

Turning pass-through network architectures into iterative ones, which use their own output as input, is a well-known approach for boosting performance. In this paper, we argue that such architectures offer an additional benefit: The convergence rate of their successive outputs is highly correlated with the accuracy of the value to which they converge. Thus, we can use the convergence rate as a useful proxy for uncertainty. This results in an approach to uncertainty estimation that provides state-of-the-art estimates at a much lower computational cost than techniques like Ensembles, and without requiring any modifications to the original iterative model. We demonstrate its practical value by embedding it in two application domains: road detection in aerial images and the estimation of aerodynamic properties of 2D and 3D shapes.

DEBOSH: Deep Bayesian Shape Optimization

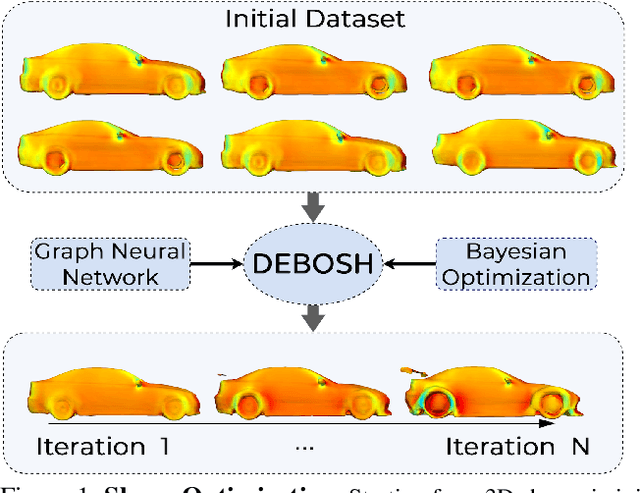
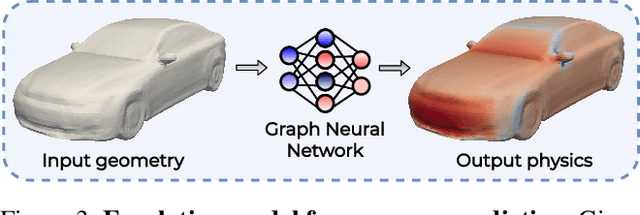
Shape optimization is at the heart of many industrial applications, such as aerodynamics, heat transfer, and structural analysis. It has recently been shown that Graph Neural Networks (GNNs) can predict the performance of a shape quickly and accurately and be used to optimize more effectively than traditional techniques that rely on response-surfaces obtained by Kriging. However, GNNs suffer from the fact that they do not evaluate their own accuracy, which is something Bayesian Optimization methods require. Therefore, estimating confidence in generated predictions is necessary to go beyond straight deterministic optimization, which is less effective. In this paper, we demonstrate that we can use Ensembles-based technique to overcome this limitation and outperform the state-of-the-art. Our experiments on diverse aerodynamics and structural analysis tasks prove that adding uncertainty to shape optimization significantly improves the quality of resulting shapes and reduces the time required for the optimization.

HybridSDF: Combining Free Form Shapes and Geometric Primitives for effective Shape Manipulation

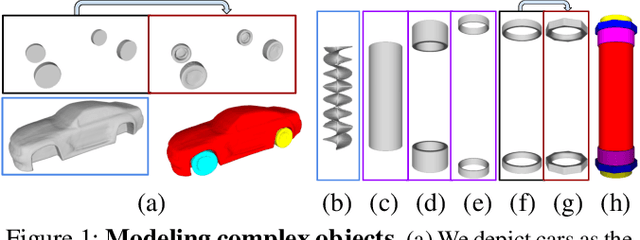
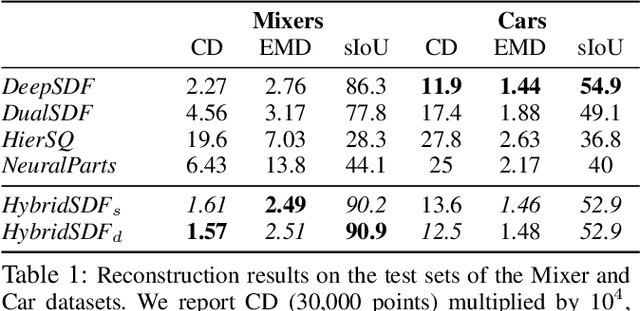
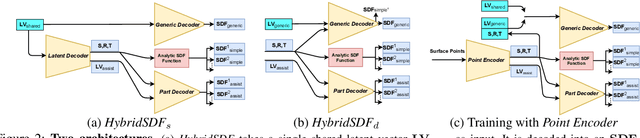
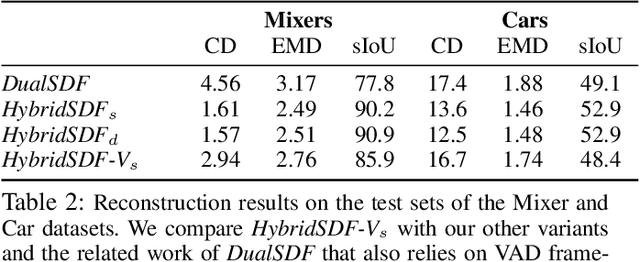
CAD modeling typically involves the use of simple geometric primitives whereas recent advances in deep-learning based 3D surface modeling have opened new shape design avenues. Unfortunately, these advances have not yet been accepted by the CAD community because they cannot be integrated into engineering workflows. To remedy this, we propose a novel approach to effectively combining geometric primitives and free-form surfaces represented by implicit surfaces for accurate modeling that preserves interpretability, enforces consistency, and enables easy manipulation.

Scaling up deep neural networks: a capacity allocation perspective

Following the recent work on capacity allocation, we formulate the conjecture that the shattering problem in deep neural networks can only be avoided if the capacity propagation through layers has a non-degenerate continuous limit when the number of layers tends to infinity. This allows us to study a number of commonly used architectures and determine which scaling relations should be enforced in practice as the number of layers grows large. In particular, we recover the conditions of Xavier initialization in the multi-channel case, and we find that weights and biases should be scaled down as the inverse square root of the number of layers for deep residual networks and as the inverse square root of the desired memory length for recurrent networks.

Capacity allocation through neural network layers

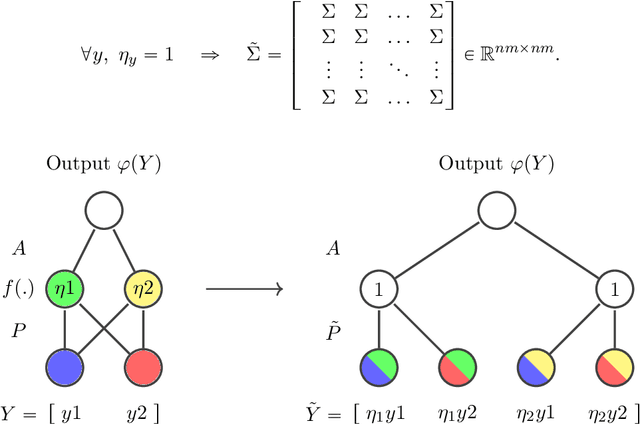
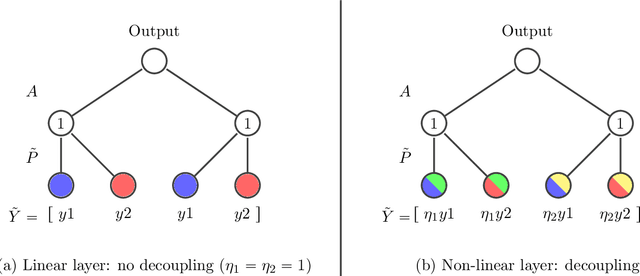
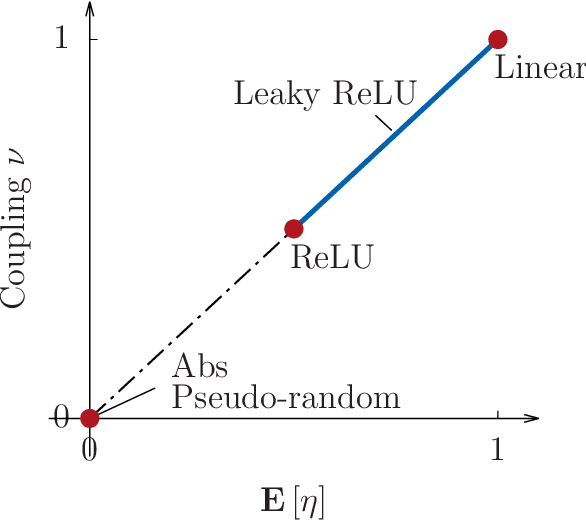
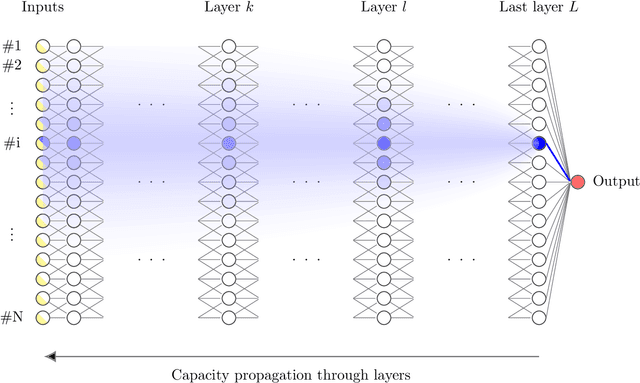
Capacity analysis has been recently introduced as a way to analyze how linear models distribute their modelling capacity across the input space. In this paper, we extend the notion of capacity allocation to the case of neural networks with non-linear layers. We show that under some hypotheses the problem is equivalent to linear capacity allocation, within some extended input space that factors in the non-linearities. We introduce the notion of layer decoupling, which quantifies the degree to which a non-linear activation decouples its outputs, and show that it plays a central role in capacity allocation through layers. In the highly non-linear limit where decoupling is total, we show that the propagation of capacity throughout the layers follows a simple markovian rule, which turns into a diffusion PDE in the limit of deep networks with residual layers. This allows us to recover some known results about deep neural networks, such as the size of the effective receptive field, or why ResNets avoid the shattering problem.

Capacity allocation analysis of neural networks: A tool for principled architecture design

Designing neural network architectures is a task that lies somewhere between science and art. For a given task, some architectures are eventually preferred over others, based on a mix of intuition, experience, experimentation and luck. For many tasks, the final word is attributed to the loss function, while for some others a further perceptual evaluation is necessary to assess and compare performance across models. In this paper, we introduce the concept of capacity allocation analysis, with the aim of shedding some light on what network architectures focus their modelling capacity on, when used on a given task. We focus more particularly on spatial capacity allocation, which analyzes a posteriori the effective number of parameters that a given model has allocated for modelling dependencies on a given point or region in the input space, in linear settings. We use this framework to perform a quantitative comparison between some classical architectures on various synthetic tasks. Finally, we consider how capacity allocation might translate in non-linear settings.