HybridSDF: Combining Free Form Shapes and Geometric Primitives for effective Shape Manipulation

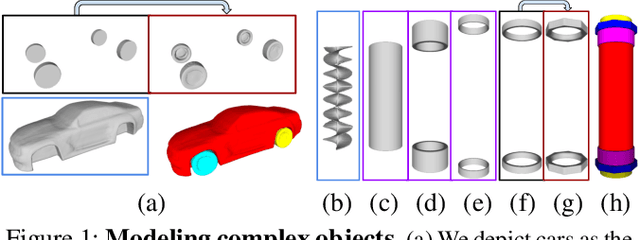
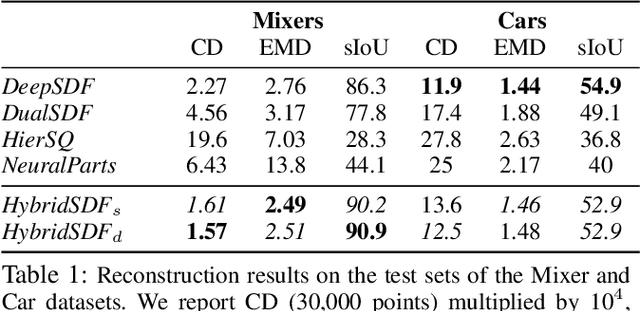
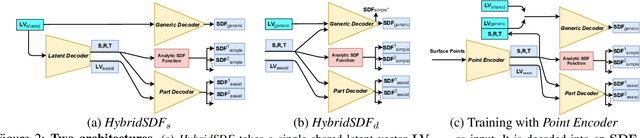
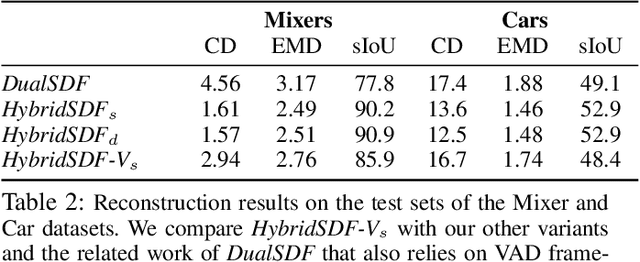
CAD modeling typically involves the use of simple geometric primitives whereas recent advances in deep-learning based 3D surface modeling have opened new shape design avenues. Unfortunately, these advances have not yet been accepted by the CAD community because they cannot be integrated into engineering workflows. To remedy this, we propose a novel approach to effectively combining geometric primitives and free-form surfaces represented by implicit surfaces for accurate modeling that preserves interpretability, enforces consistency, and enables easy manipulation.

DeepMesh: Differentiable Iso-Surface Extraction

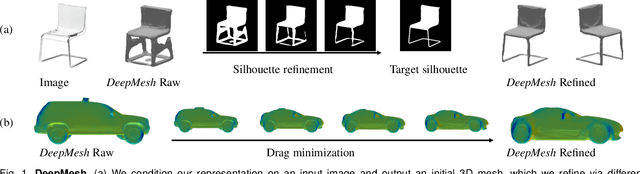
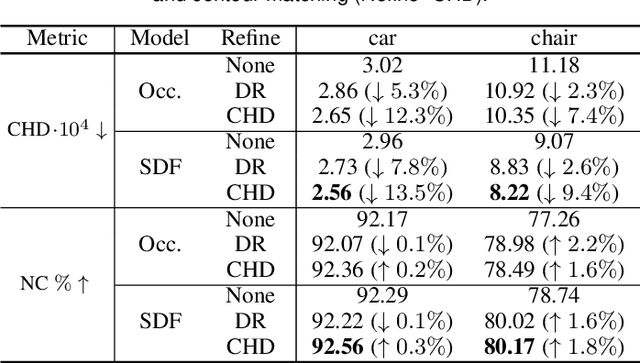
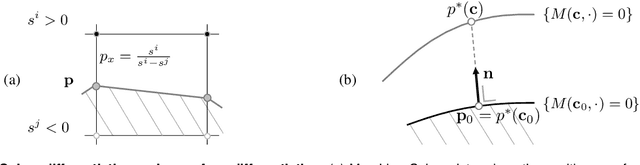
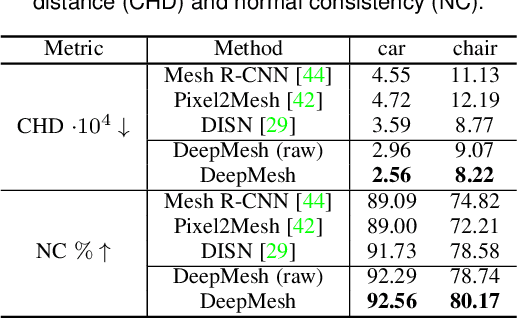
Geometric Deep Learning has recently made striking progress with the advent of continuous Deep Implicit Fields. They allow for detailed modeling of watertight surfaces of arbitrary topology while not relying on a 3D Euclidean grid, resulting in a learnable parameterization that is unlimited in resolution. Unfortunately, these methods are often unsuitable for applications that require an explicit mesh-based surface representation because converting an implicit field to such a representation relies on the Marching Cubes algorithm, which cannot be differentiated with respect to the underlying implicit field. In this work, we remove this limitation and introduce a differentiable way to produce explicit surface mesh representations from Deep Implicit Fields. Our key insight is that by reasoning on how implicit field perturbations impact local surface geometry, one can ultimately differentiate the 3D location of surface samples with respect to the underlying deep implicit field. We exploit this to define DeepMesh -- end-to-end differentiable mesh representation that can vary its topology. We use two different applications to validate our theoretical insight: Single view 3D Reconstruction via Differentiable Rendering and Physically-Driven Shape Optimization. In both cases our end-to-end differentiable parameterization gives us an edge over state-of-the-art algorithms.

Masksembles for Uncertainty Estimation

Deep neural networks have amply demonstrated their prowess but estimating the reliability of their predictions remains challenging. Deep Ensembles are widely considered as being one of the best methods for generating uncertainty estimates but are very expensive to train and evaluate. MC-Dropout is another popular alternative, which is less expensive, but also less reliable. Our central intuition is that there is a continuous spectrum of ensemble-like models of which MC-Dropout and Deep Ensembles are extreme examples. The first uses an effectively infinite number of highly correlated models while the second relies on a finite number of independent models. To combine the benefits of both, we introduce Masksembles. Instead of randomly dropping parts of the network as in MC-dropout, Masksemble relies on a fixed number of binary masks, which are parameterized in a way that allows to change correlations between individual models. Namely, by controlling the overlap between the masks and their density one can choose the optimal configuration for the task at hand. This leads to a simple and easy to implement method with performance on par with Ensembles at a fraction of the cost. We experimentally validate Masksembles on two widely used datasets, CIFAR10 and ImageNet.

MeshSDF: Differentiable Iso-Surface Extraction

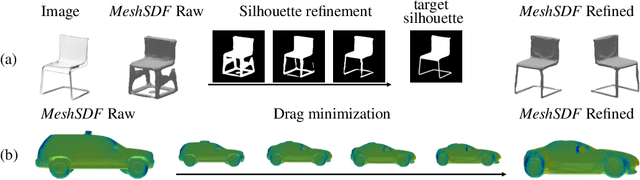
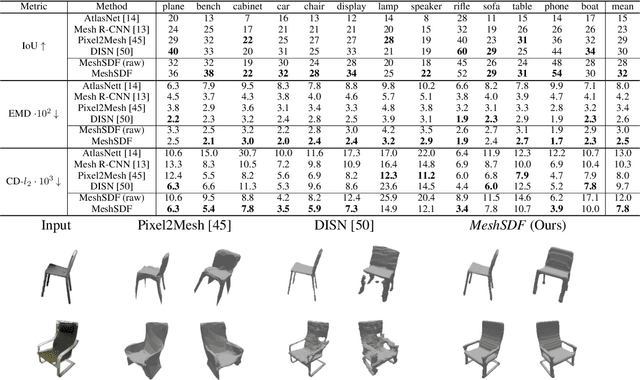
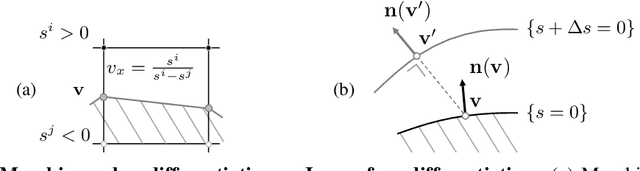
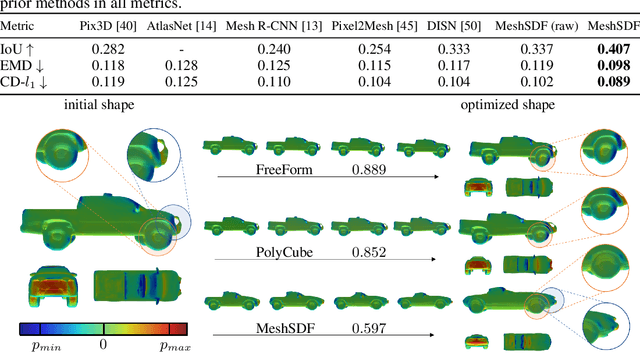
Geometric Deep Learning has recently made striking progress with the advent of continuous Deep Implicit Fields. They allow for detailed modeling of watertight surfaces of arbitrary topology while not relying on a 3D Euclidean grid, resulting in a learnable parameterization that is not limited in resolution. Unfortunately, these methods are often not suitable for applications that require an explicit mesh-based surface representation because converting an implicit field to such a representation relies on the Marching Cubes algorithm, which cannot be differentiated with respect to the underlying implicit field. In this work, we remove this limitation and introduce a differentiable way to produce explicit surface mesh representations from Deep Signed Distance Functions. Our key insight is that by reasoning on how implicit field perturbations impact local surface geometry, one can ultimately differentiate the 3D location of surface samples with respect to the underlying deep implicit field. We exploit this to define MeshSDF, an end-to-end differentiable mesh representation which can vary its topology. We use two different applications to validate our theoretical insight: Single-View Reconstruction via Differentiable Rendering and Physically-Driven Shape Optimization. In both cases our differentiable parameterization gives us an edge over state-of-the-art algorithms.

NeuralSampler: Euclidean Point Cloud Auto-Encoder and Sampler

Most algorithms that rely on deep learning-based approaches to generate 3D point sets can only produce clouds containing fixed number of points. Furthermore, they typically require large networks parameterized by many weights, which makes them hard to train. In this paper, we propose an auto-encoder architecture that can both encode and decode clouds of arbitrary size and demonstrate its effectiveness at upsampling sparse point clouds. Interestingly, we can do so using less than half as many parameters as state-of-the-art architectures while still delivering better performance. We will make our code base fully available.