Capacity allocation through neural network layers
Paper and Code
Feb 27, 2019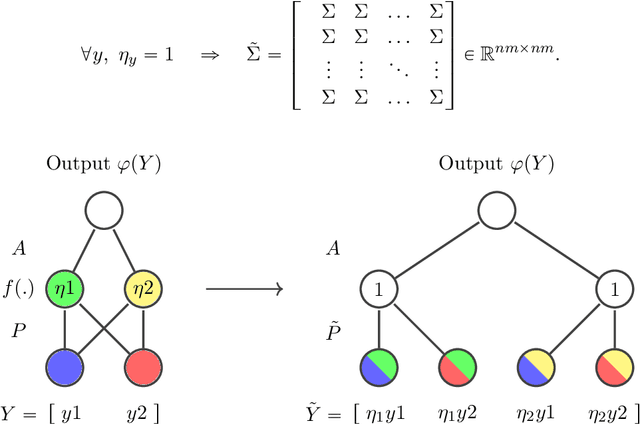
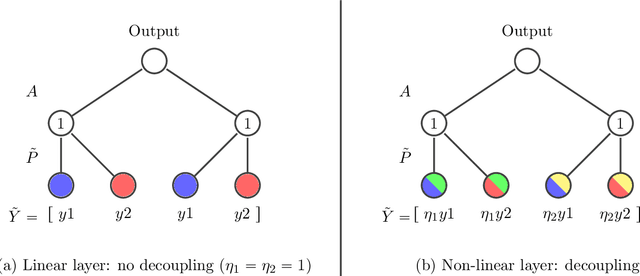
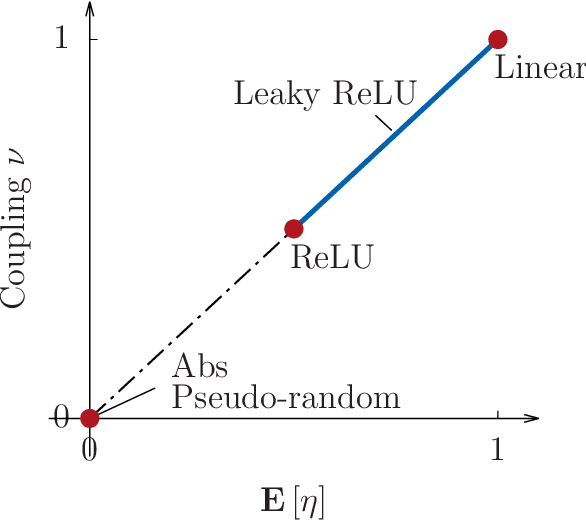
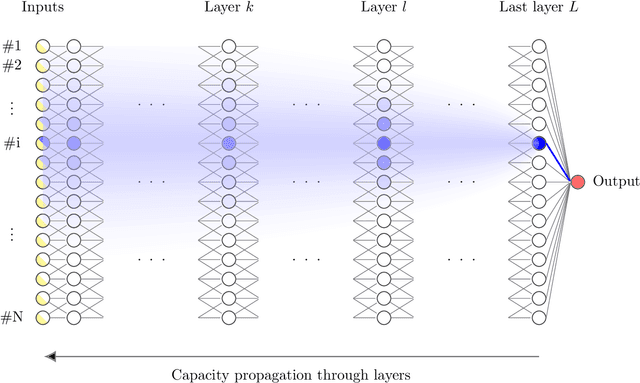
Capacity analysis has been recently introduced as a way to analyze how linear models distribute their modelling capacity across the input space. In this paper, we extend the notion of capacity allocation to the case of neural networks with non-linear layers. We show that under some hypotheses the problem is equivalent to linear capacity allocation, within some extended input space that factors in the non-linearities. We introduce the notion of layer decoupling, which quantifies the degree to which a non-linear activation decouples its outputs, and show that it plays a central role in capacity allocation through layers. In the highly non-linear limit where decoupling is total, we show that the propagation of capacity throughout the layers follows a simple markovian rule, which turns into a diffusion PDE in the limit of deep networks with residual layers. This allows us to recover some known results about deep neural networks, such as the size of the effective receptive field, or why ResNets avoid the shattering problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge