Bayesian Sheaf Neural Networks

Equipping graph neural networks with a convolution operation defined in terms of a cellular sheaf offers advantages for learning expressive representations of heterophilic graph data. The most flexible approach to constructing the sheaf is to learn it as part of the network as a function of the node features. However, this leaves the network potentially overly sensitive to the learned sheaf. As a counter-measure, we propose a variational approach to learning cellular sheaves within sheaf neural networks, yielding an architecture we refer to as a Bayesian sheaf neural network. As part of this work, we define a novel family of reparameterizable probability distributions on the rotation group $SO(n)$ using the Cayley transform. We evaluate the Bayesian sheaf neural network on several graph datasets, and show that our Bayesian sheaf models outperform deterministic sheaf models when training data is limited, and are less sensitive to the choice of hyperparameters.

Monitoring Drug-Induced Brain Activity Changes with Functional Ultrasound Imaging and Convolutional Neural Networks

Functional ultrasound imaging (fUSI) is a cutting-edge technology that measures changes in cerebral blood volume (CBV) by detecting backscattered echoes from red blood cells moving within its field of view (FOV). It offers high spatiotemporal resolution and sensitivity, allowing for detailed visualization of cerebral blood flow dynamics. While fUSI has been utilized in preclinical drug development studies to explore the mechanisms of action of various drugs targeting the central nervous system, many of these studies have primarily focused on predetermined regions of interest (ROIs). This focus may overlook relevant brain activity outside these specific areas, which could influence the results. To address this limitation, we combined convolutional neural networks (CNNs) with fUSI to comprehensively understand the pharmacokinetic process of Dizocilpine, also known as MK-801, a drug that blocks the N-Methyl-D-aspartate (NMDA) receptor in the central nervous system. CNN and class activation mapping (CAM) revealed the spatiotemporal effects of MK-801, which originated in the cortex and propagated to the hippocampus, demonstrating the ability to detect dynamic drug effects over time. Additionally, CNN and CAM assessed the impact of anesthesia on the spatiotemporal hemodynamics of the brain, revealing no distinct patterns between early and late stages. The integration of fUSI and CNN provides a powerful tool to gain insights into the spatiotemporal dynamics of drug action in the brain. This combination enables a comprehensive and unbiased assessment of drug effects on brain function, potentially accelerating the development of new therapies in neuropharmacological studies.

Geometric sparsification in recurrent neural networks

A common technique for ameliorating the computational costs of running large neural models is sparsification, or the removal of neural connections during training. Sparse models are capable of maintaining the high accuracy of state of the art models, while functioning at the cost of more parsimonious models. The structures which underlie sparse architectures are, however, poorly understood and not consistent between differently trained models and sparsification schemes. In this paper, we propose a new technique for sparsification of recurrent neural nets (RNNs), called moduli regularization, in combination with magnitude pruning. Moduli regularization leverages the dynamical system induced by the recurrent structure to induce a geometric relationship between neurons in the hidden state of the RNN. By making our regularizing term explicitly geometric, we provide the first, to our knowledge, a priori description of the desired sparse architecture of our neural net. We verify the effectiveness of our scheme for navigation and natural language processing RNNs. Navigation is a structurally geometric task, for which there are known moduli spaces, and we show that regularization can be used to reach 90% sparsity while maintaining model performance only when coefficients are chosen in accordance with a suitable moduli space. Natural language processing, however, has no known moduli space in which computations are performed. Nevertheless, we show that moduli regularization induces more stable recurrent neural nets with a variety of moduli regularizers, and achieves high fidelity models at 98% sparsity.

Quantum Distance Approximation for Persistence Diagrams

Topological Data Analysis methods can be useful for classification and clustering tasks in many different fields as they can provide two dimensional persistence diagrams that summarize important information about the shape of potentially complex and high dimensional data sets. The space of persistence diagrams can be endowed with various metrics such as the Wasserstein distance which admit a statistical structure and allow to use these summaries for machine learning algorithms. However, computing the distance between two persistence diagrams involves finding an optimal way to match the points of the two diagrams and may not always be an easy task for classical computers. In this work we explore the potential of quantum computers to estimate the distance between persistence diagrams, in particular we propose variational quantum algorithms for the Wasserstein distance as well as the $d^{c}_{p}$ distance. Our implementation is a weighted version of the Quantum Approximate Optimization Algorithm that relies on control clauses to encode the constraints of the optimization problem.

Position Paper: Challenges and Opportunities in Topological Deep Learning

Topological deep learning (TDL) is a rapidly evolving field that uses topological features to understand and design deep learning models. This paper posits that TDL may complement graph representation learning and geometric deep learning by incorporating topological concepts, and can thus provide a natural choice for various machine learning settings. To this end, this paper discusses open problems in TDL, ranging from practical benefits to theoretical foundations. For each problem, it outlines potential solutions and future research opportunities. At the same time, this paper serves as an invitation to the scientific community to actively participate in TDL research to unlock the potential of this emerging field.

A Topological Deep Learning Framework for Neural Spike Decoding

The brain's spatial orientation system uses different neuron ensembles to aid in environment-based navigation. One of the ways brains encode spatial information is through grid cells, layers of decked neurons that overlay to provide environment-based navigation. These neurons fire in ensembles where several neurons fire at once to activate a single grid. We want to capture this firing structure and use it to decode grid cell data. Understanding, representing, and decoding these neural structures require models that encompass higher order connectivity than traditional graph-based models may provide. To that end, in this work, we develop a topological deep learning framework for neural spike train decoding. Our framework combines unsupervised simplicial complex discovery with the power of deep learning via a new architecture we develop herein called a simplicial convolutional recurrent neural network (SCRNN). Simplicial complexes, topological spaces that use not only vertices and edges but also higher-dimensional objects, naturally generalize graphs and capture more than just pairwise relationships. Additionally, this approach does not require prior knowledge of the neural activity beyond spike counts, which removes the need for similarity measurements. The effectiveness and versatility of the SCRNN is demonstrated on head direction data to test its performance and then applied to grid cell datasets with the task to automatically predict trajectories.

Quantum Persistent Homology for Time Series

Persistent homology, a powerful mathematical tool for data analysis, summarizes the shape of data through tracking topological features across changes in different scales. Classical algorithms for persistent homology are often constrained by running times and memory requirements that grow exponentially on the number of data points. To surpass this problem, two quantum algorithms of persistent homology have been developed based on two different approaches. However, both of these quantum algorithms consider a data set in the form of a point cloud, which can be restrictive considering that many data sets come in the form of time series. In this paper, we alleviate this issue by establishing a quantum Takens's delay embedding algorithm, which turns a time series into a point cloud by considering a pertinent embedding into a higher dimensional space. Having this quantum transformation of time series to point clouds, then one may use a quantum persistent homology algorithm to extract the topological features from the point cloud associated with the original times series.

Random Persistence Diagram Generation

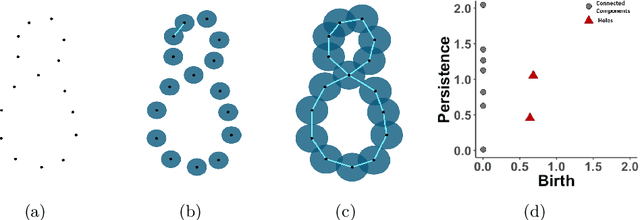
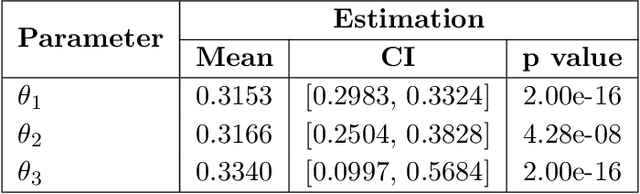
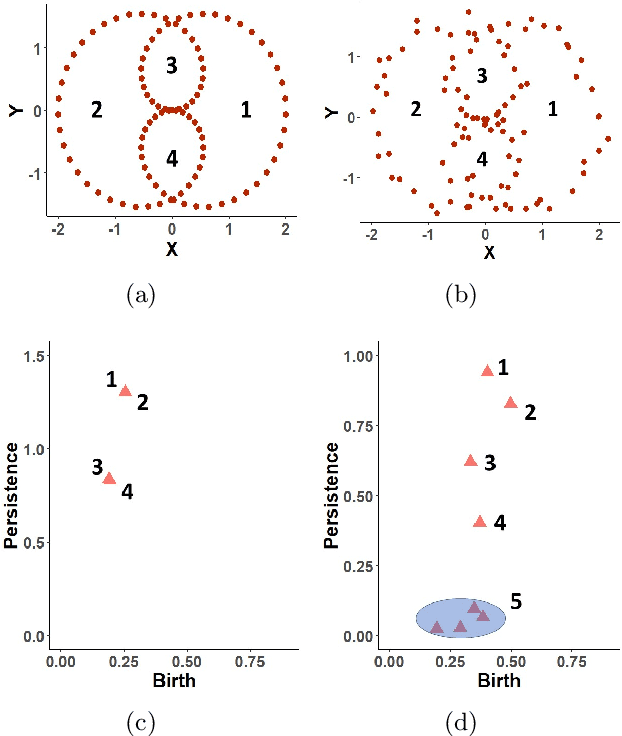
Topological data analysis (TDA) studies the shape patterns of data. Persistent homology (PH) is a widely used method in TDA that summarizes homological features of data at multiple scales and stores this in persistence diagrams (PDs). As TDA is commonly used in the analysis of high dimensional data sets, a sufficiently large amount of PDs that allow performing statistical analysis is typically unavailable or requires inordinate computational resources. In this paper, we propose random persistence diagram generation (RPDG), a method that generates a sequence of random PDs from the ones produced by the data. RPDG is underpinned (i) by a parametric model based on pairwise interacting point processes for inference of persistence diagrams and (ii) by a reversible jump Markov chain Monte Carlo (RJ-MCMC) algorithm for generating samples of PDs. The parametric model combines a Dirichlet partition to capture spatial homogeneity of the location of points in a PD and a step function to capture the pairwise interaction between them. The RJ-MCMC algorithm incorporates trans-dimensional addition and removal of points and same-dimensional relocation of points across samples of PDs. The efficacy of RPDG is demonstrated via an example and a detailed comparison with other existing methods is presented.

Materials Fingerprinting Classification

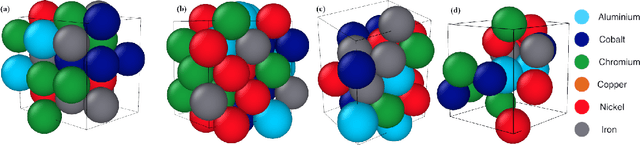
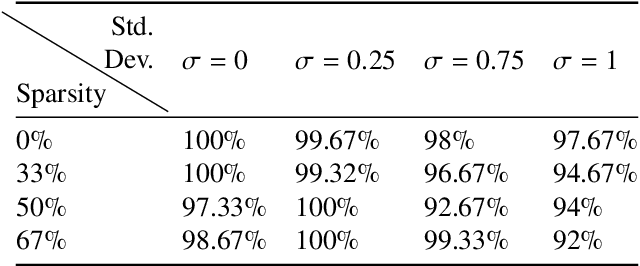
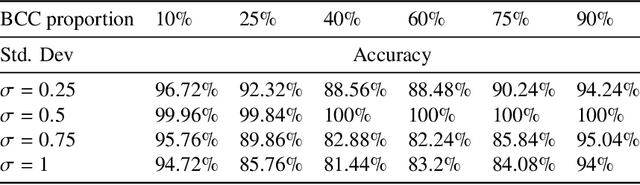
Significant progress in many classes of materials could be made with the availability of experimentally-derived large datasets composed of atomic identities and three-dimensional coordinates. Methods for visualizing the local atomic structure, such as atom probe tomography (APT), which routinely generate datasets comprised of millions of atoms, are an important step in realizing this goal. However, state-of-the-art APT instruments generate noisy and sparse datasets that provide information about elemental type, but obscure atomic structures, thus limiting their subsequent value for materials discovery. The application of a materials fingerprinting process, a machine learning algorithm coupled with topological data analysis, provides an avenue by which here-to-fore unprecedented structural information can be extracted from an APT dataset. As a proof of concept, the material fingerprint is applied to high-entropy alloy APT datasets containing body-centered cubic (BCC) and face-centered cubic (FCC) crystal structures. A local atomic configuration centered on an arbitrary atom is assigned a topological descriptor, with which it can be characterized as a BCC or FCC lattice with near perfect accuracy, despite the inherent noise in the dataset. This successful identification of a fingerprint is a crucial first step in the development of algorithms which can extract more nuanced information, such as chemical ordering, from existing datasets of complex materials.

Topological Deep Learning

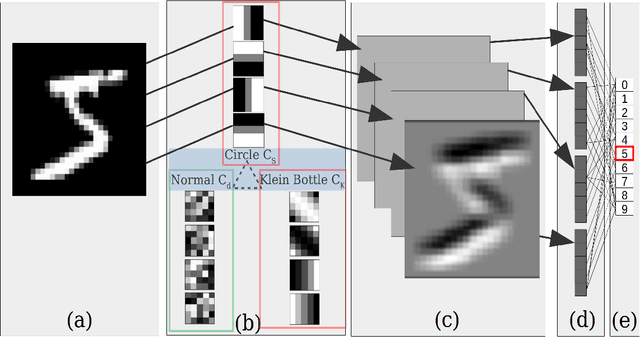
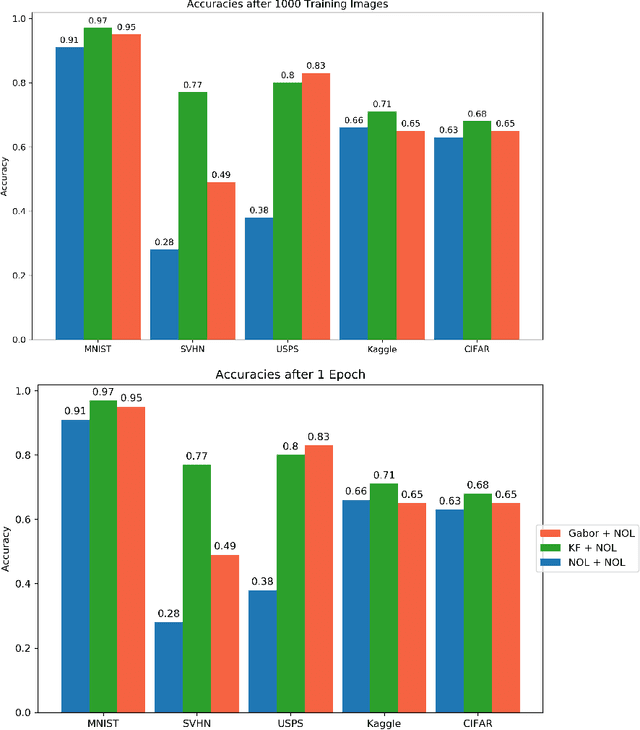
This work introduces the Topological CNN (TCNN), which encompasses several topologically defined convolutional methods. Manifolds with important relationships to the natural image space are used to parameterize image filters which are used as convolutional weights in a TCNN. These manifolds also parameterize slices in layers of a TCNN across which the weights are localized. We show evidence that TCNNs learn faster, on less data, with fewer learned parameters, and with greater generalizability and interpretability than conventional CNNs. We introduce and explore TCNN layers for both image and video data. We propose extensions to 3D images and 3D video.