Materials Fingerprinting Classification

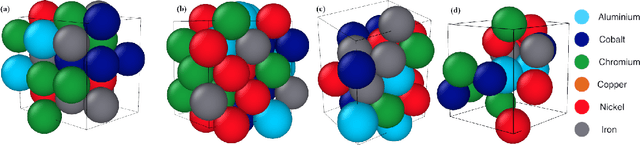
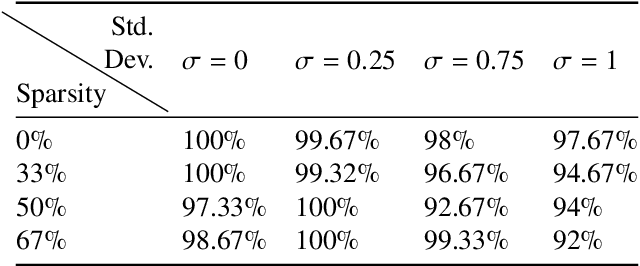
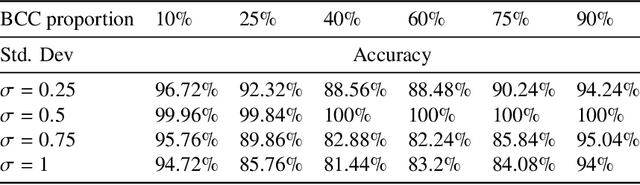
Significant progress in many classes of materials could be made with the availability of experimentally-derived large datasets composed of atomic identities and three-dimensional coordinates. Methods for visualizing the local atomic structure, such as atom probe tomography (APT), which routinely generate datasets comprised of millions of atoms, are an important step in realizing this goal. However, state-of-the-art APT instruments generate noisy and sparse datasets that provide information about elemental type, but obscure atomic structures, thus limiting their subsequent value for materials discovery. The application of a materials fingerprinting process, a machine learning algorithm coupled with topological data analysis, provides an avenue by which here-to-fore unprecedented structural information can be extracted from an APT dataset. As a proof of concept, the material fingerprint is applied to high-entropy alloy APT datasets containing body-centered cubic (BCC) and face-centered cubic (FCC) crystal structures. A local atomic configuration centered on an arbitrary atom is assigned a topological descriptor, with which it can be characterized as a BCC or FCC lattice with near perfect accuracy, despite the inherent noise in the dataset. This successful identification of a fingerprint is a crucial first step in the development of algorithms which can extract more nuanced information, such as chemical ordering, from existing datasets of complex materials.

Bayesian Topological Learning for Classifying the Structure of Biological Networks

Actin cytoskeleton networks generate local topological signatures due to the natural variations in the number, size, and shape of holes of the networks. Persistent homology is a method that explores these topological properties of data and summarizes them as persistence diagrams. In this work, we analyze and classify these filament networks by transforming them into persistence diagrams whose variability is quantified via a Bayesian framework on the space of persistence diagrams. The proposed generalized Bayesian framework adopts an independent and identically distributed cluster point process characterization of persistence diagrams and relies on a substitution likelihood argument. This framework provides the flexibility to estimate the posterior cardinality distribution of points in a persistence diagram and the posterior spatial distribution simultaneously. We present a closed form of the posteriors under the assumption of Gaussian mixtures and binomials for prior intensity and cardinality respectively. Using this posterior calculation, we implement a Bayes factor algorithm to classify the actin filament networks and benchmark it against several state-of-the-art classification methods.

A Stable Cardinality Distance for Topological Classification

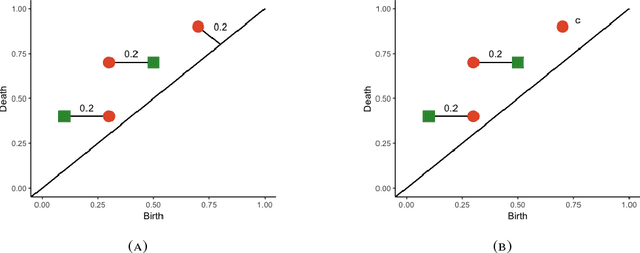
This work incorporates topological and geometric features via persistence diagrams to classify point cloud data arising from materials science. Persistence diagrams are planar sets that summarize the shape details of given data. A new metric on persistence diagrams generates input features for the classification algorithm. The metric accounts for the similarity of persistence diagrams using a linear combination of matching costs and cardinality differences. Investigation of the stability properties of this metric provides theoretical justification for the use of the metric for comparisons of such diagrams. The crystal structure of materials are successfully classified based on noisy and sparse data retrieved from synthetic Atomic Probe Tomography experiments.