Global explainability of a deep abstaining classifier

We present a global explainability method to characterize sources of errors in the histology prediction task of our real-world multitask convolutional neural network (MTCNN)-based deep abstaining classifier (DAC), for automated annotation of cancer pathology reports from NCI-SEER registries. Our classifier was trained and evaluated on 1.04 million hand-annotated samples and makes simultaneous predictions of cancer site, subsite, histology, laterality, and behavior for each report. The DAC framework enables the model to abstain on ambiguous reports and/or confusing classes to achieve a target accuracy on the retained (non-abstained) samples, but at the cost of decreased coverage. Requiring 97% accuracy on the histology task caused our model to retain only 22% of all samples, mostly the less ambiguous and common classes. Local explainability with the GradInp technique provided a computationally efficient way of obtaining contextual reasoning for thousands of individual predictions. Our method, involving dimensionality reduction of approximately 13000 aggregated local explanations, enabled global identification of sources of errors as hierarchical complexity among classes, label noise, insufficient information, and conflicting evidence. This suggests several strategies such as exclusion criteria, focused annotation, and reduced penalties for errors involving hierarchically related classes to iteratively improve our DAC in this complex real-world implementation.

Topological Interpretability for Deep-Learning

With the increasing adoption of AI-based systems across everyday life, the need to understand their decision-making mechanisms is correspondingly accelerating. The level at which we can trust the statistical inferences made from AI-based decision systems is an increasing concern, especially in high-risk systems such as criminal justice or medical diagnosis, where incorrect inferences may have tragic consequences. Despite their successes in providing solutions to problems involving real-world data, deep learning (DL) models cannot quantify the certainty of their predictions. And are frequently quite confident, even when their solutions are incorrect. This work presents a method to infer prominent features in two DL classification models trained on clinical and non-clinical text by employing techniques from topological and geometric data analysis. We create a graph of a model's prediction space and cluster the inputs into the graph's vertices by the similarity of features and prediction statistics. We then extract subgraphs demonstrating high-predictive accuracy for a given label. These subgraphs contain a wealth of information about features that the DL model has recognized as relevant to its decisions. We infer these features for a given label using a distance metric between probability measures, and demonstrate the stability of our method compared to the LIME interpretability method. This work demonstrates that we may gain insights into the decision mechanism of a DL model, which allows us to ascertain if the model is making its decisions based on information germane to the problem or identifies extraneous patterns within the data.

Materials Fingerprinting Classification

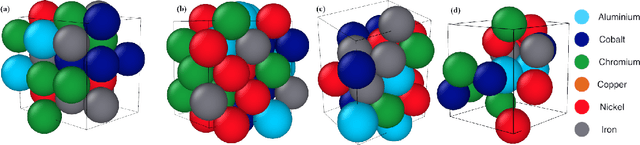
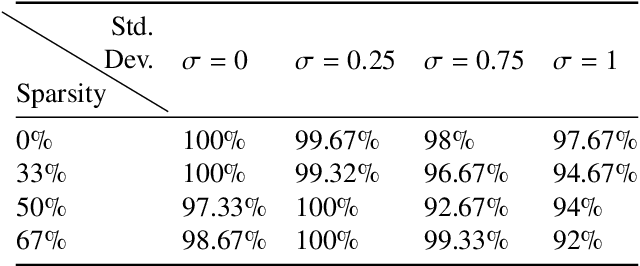
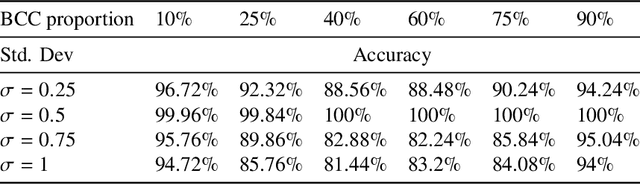
Significant progress in many classes of materials could be made with the availability of experimentally-derived large datasets composed of atomic identities and three-dimensional coordinates. Methods for visualizing the local atomic structure, such as atom probe tomography (APT), which routinely generate datasets comprised of millions of atoms, are an important step in realizing this goal. However, state-of-the-art APT instruments generate noisy and sparse datasets that provide information about elemental type, but obscure atomic structures, thus limiting their subsequent value for materials discovery. The application of a materials fingerprinting process, a machine learning algorithm coupled with topological data analysis, provides an avenue by which here-to-fore unprecedented structural information can be extracted from an APT dataset. As a proof of concept, the material fingerprint is applied to high-entropy alloy APT datasets containing body-centered cubic (BCC) and face-centered cubic (FCC) crystal structures. A local atomic configuration centered on an arbitrary atom is assigned a topological descriptor, with which it can be characterized as a BCC or FCC lattice with near perfect accuracy, despite the inherent noise in the dataset. This successful identification of a fingerprint is a crucial first step in the development of algorithms which can extract more nuanced information, such as chemical ordering, from existing datasets of complex materials.

A Stable Cardinality Distance for Topological Classification

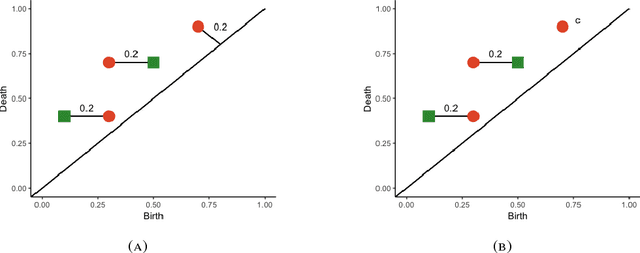
This work incorporates topological and geometric features via persistence diagrams to classify point cloud data arising from materials science. Persistence diagrams are planar sets that summarize the shape details of given data. A new metric on persistence diagrams generates input features for the classification algorithm. The metric accounts for the similarity of persistence diagrams using a linear combination of matching costs and cardinality differences. Investigation of the stability properties of this metric provides theoretical justification for the use of the metric for comparisons of such diagrams. The crystal structure of materials are successfully classified based on noisy and sparse data retrieved from synthetic Atomic Probe Tomography experiments.