Position Paper: Challenges and Opportunities in Topological Deep Learning

Topological deep learning (TDL) is a rapidly evolving field that uses topological features to understand and design deep learning models. This paper posits that TDL may complement graph representation learning and geometric deep learning by incorporating topological concepts, and can thus provide a natural choice for various machine learning settings. To this end, this paper discusses open problems in TDL, ranging from practical benefits to theoretical foundations. For each problem, it outlines potential solutions and future research opportunities. At the same time, this paper serves as an invitation to the scientific community to actively participate in TDL research to unlock the potential of this emerging field.

Random Persistence Diagram Generation

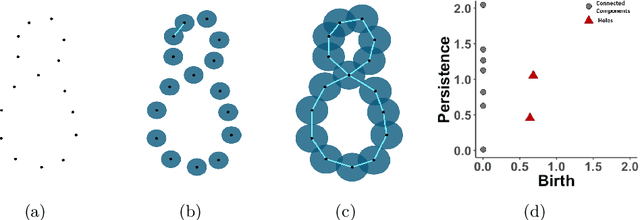
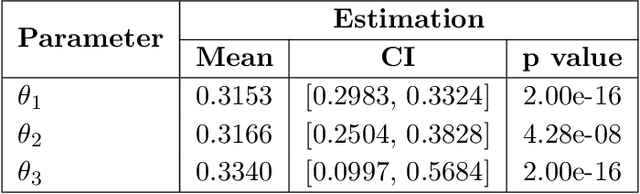
Topological data analysis (TDA) studies the shape patterns of data. Persistent homology (PH) is a widely used method in TDA that summarizes homological features of data at multiple scales and stores this in persistence diagrams (PDs). As TDA is commonly used in the analysis of high dimensional data sets, a sufficiently large amount of PDs that allow performing statistical analysis is typically unavailable or requires inordinate computational resources. In this paper, we propose random persistence diagram generation (RPDG), a method that generates a sequence of random PDs from the ones produced by the data. RPDG is underpinned (i) by a parametric model based on pairwise interacting point processes for inference of persistence diagrams and (ii) by a reversible jump Markov chain Monte Carlo (RJ-MCMC) algorithm for generating samples of PDs. The parametric model combines a Dirichlet partition to capture spatial homogeneity of the location of points in a PD and a step function to capture the pairwise interaction between them. The RJ-MCMC algorithm incorporates trans-dimensional addition and removal of points and same-dimensional relocation of points across samples of PDs. The efficacy of RPDG is demonstrated via an example and a detailed comparison with other existing methods is presented.

Materials Fingerprinting Classification

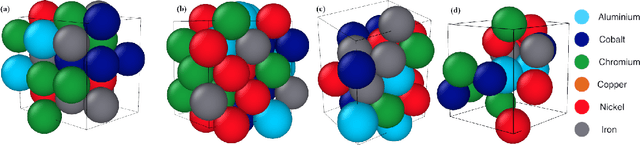
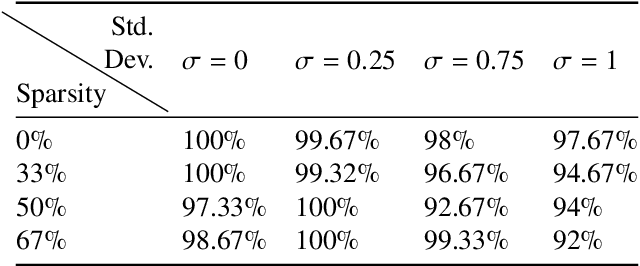
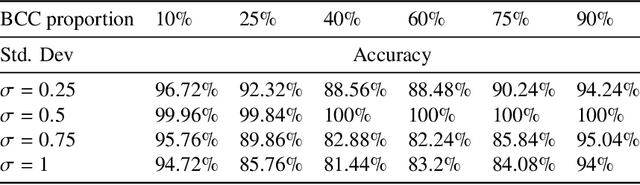
Significant progress in many classes of materials could be made with the availability of experimentally-derived large datasets composed of atomic identities and three-dimensional coordinates. Methods for visualizing the local atomic structure, such as atom probe tomography (APT), which routinely generate datasets comprised of millions of atoms, are an important step in realizing this goal. However, state-of-the-art APT instruments generate noisy and sparse datasets that provide information about elemental type, but obscure atomic structures, thus limiting their subsequent value for materials discovery. The application of a materials fingerprinting process, a machine learning algorithm coupled with topological data analysis, provides an avenue by which here-to-fore unprecedented structural information can be extracted from an APT dataset. As a proof of concept, the material fingerprint is applied to high-entropy alloy APT datasets containing body-centered cubic (BCC) and face-centered cubic (FCC) crystal structures. A local atomic configuration centered on an arbitrary atom is assigned a topological descriptor, with which it can be characterized as a BCC or FCC lattice with near perfect accuracy, despite the inherent noise in the dataset. This successful identification of a fingerprint is a crucial first step in the development of algorithms which can extract more nuanced information, such as chemical ordering, from existing datasets of complex materials.

Bayesian Topological Learning for Classifying the Structure of Biological Networks

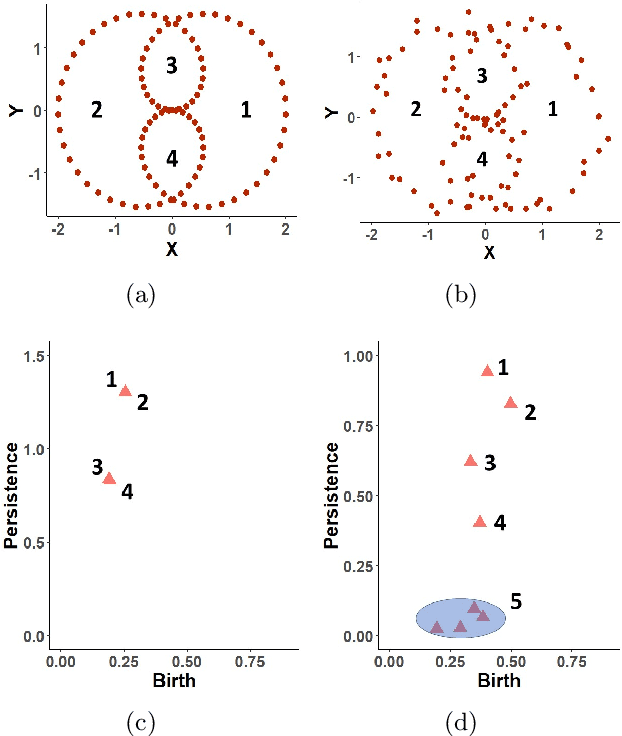
Actin cytoskeleton networks generate local topological signatures due to the natural variations in the number, size, and shape of holes of the networks. Persistent homology is a method that explores these topological properties of data and summarizes them as persistence diagrams. In this work, we analyze and classify these filament networks by transforming them into persistence diagrams whose variability is quantified via a Bayesian framework on the space of persistence diagrams. The proposed generalized Bayesian framework adopts an independent and identically distributed cluster point process characterization of persistence diagrams and relies on a substitution likelihood argument. This framework provides the flexibility to estimate the posterior cardinality distribution of points in a persistence diagram and the posterior spatial distribution simultaneously. We present a closed form of the posteriors under the assumption of Gaussian mixtures and binomials for prior intensity and cardinality respectively. Using this posterior calculation, we implement a Bayes factor algorithm to classify the actin filament networks and benchmark it against several state-of-the-art classification methods.

Bayesian Topological Learning for Brain State Classification

Investigation of human brain states through electroencephalograph (EEG) signals is a crucial step in human-machine communications. However, classifying and analyzing EEG signals are challenging due to their noisy, nonlinear and nonstationary nature. Current methodologies for analyzing these signals often fall short because they have several regularity assumptions baked in. This work provides an effective, flexible and noise-resilient scheme to analyze EEG by extracting pertinent information while abiding by the 3N (noisy, nonlinear and nonstationary) nature of data. We implement a topological tool, namely persistent homology, that tracks the evolution of topological features over time intervals and incorporates individual's expectations as prior knowledge by means of a Bayesian framework to compute posterior distributions. Relying on these posterior distributions, we apply Bayes factor classification to noisy EEG measurements. The performance of this Bayesian classification scheme is then compared with other existing methods for EEG signals.