Topological Deep Learning

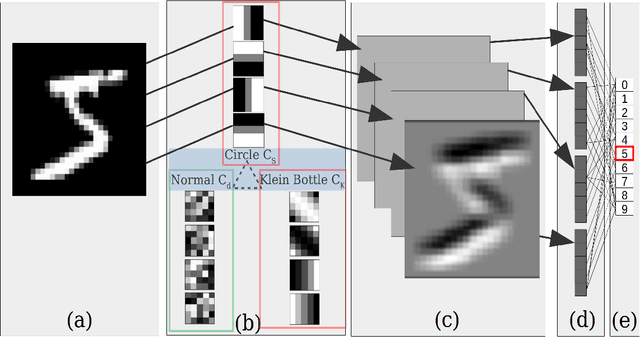
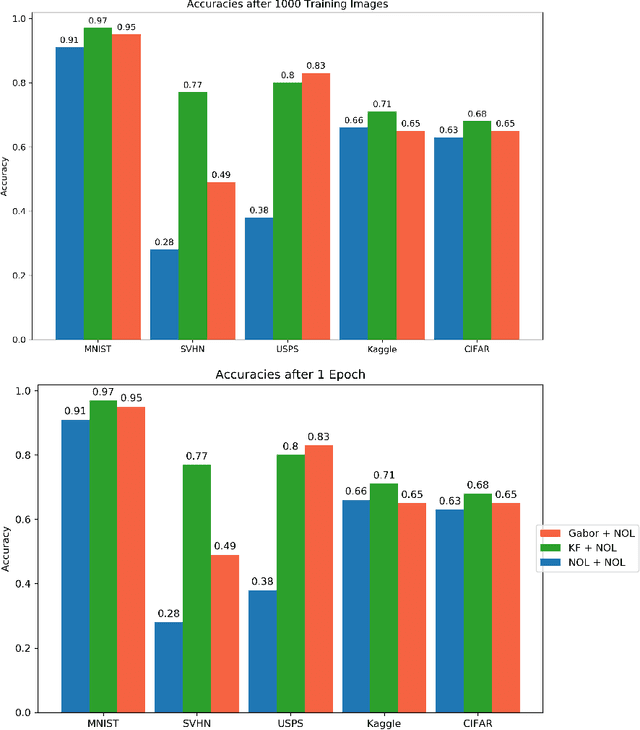
This work introduces the Topological CNN (TCNN), which encompasses several topologically defined convolutional methods. Manifolds with important relationships to the natural image space are used to parameterize image filters which are used as convolutional weights in a TCNN. These manifolds also parameterize slices in layers of a TCNN across which the weights are localized. We show evidence that TCNNs learn faster, on less data, with fewer learned parameters, and with greater generalizability and interpretability than conventional CNNs. We introduce and explore TCNN layers for both image and video data. We propose extensions to 3D images and 3D video.

The space of sections of a smooth function

Given a compact manifold $X$ with boundary and a submersion $f : X \rightarrow Y$ whose restriction to the boundary of $X$ has isolated critical points with distinct critical values and where $Y$ is $[0,1]$ or $S^1$, the connected components of the space of sections of $f$ are computed from $\pi_0$ and $\pi_1$ of the fibers of $f$. This computation is then leveraged to provide new results on a smoothed version of the evasion path problem for mobile sensor networks: From the time-varying homology of the covered region and the time-varying cup-product on cohomology of the boundary, a necessary and sufficient condition for existence of an evasion path and a lower bound on the number of homotopy classes of evasion paths are computed. No connectivity assumptions are required.