Mixup Barcodes: Quantifying Geometric-Topological Interactions between Point Clouds

We combine standard persistent homology with image persistent homology to define a novel way of characterizing shapes and interactions between them. In particular, we introduce: (1) a mixup barcode, which captures geometric-topological interactions (mixup) between two point sets in arbitrary dimension; (2) simple summary statistics, total mixup and total percentage mixup, which quantify the complexity of the interactions as a single number; (3) a software tool for playing with the above. As a proof of concept, we apply this tool to a problem arising from machine learning. In particular, we study the disentanglement in embeddings of different classes. The results suggest that topological mixup is a useful method for characterizing interactions for low and high-dimensional data. Compared to the typical usage of persistent homology, the new tool is sensitive to the geometric locations of the topological features, which is often desirable.

Activation Landscapes as a Topological Summary of Neural Network Performance

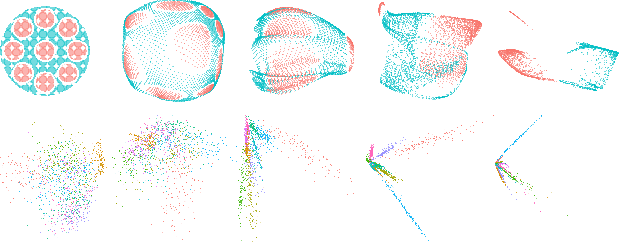
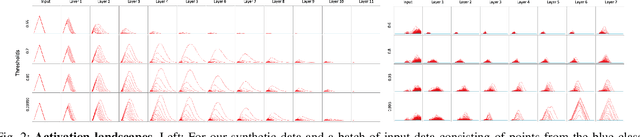
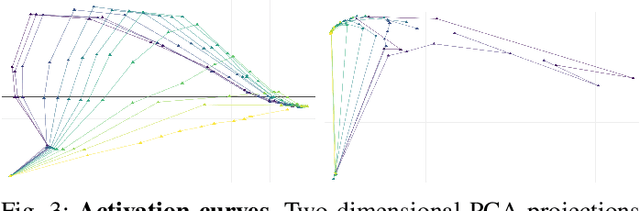
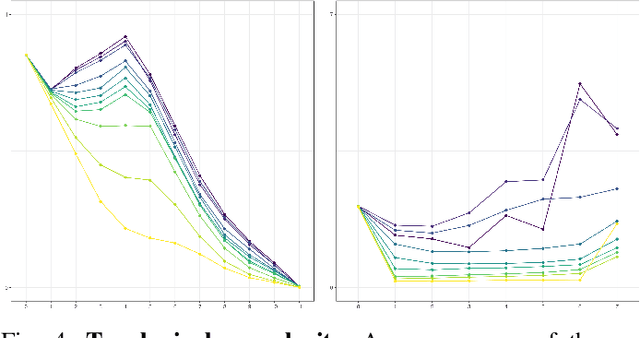
We use topological data analysis (TDA) to study how data transforms as it passes through successive layers of a deep neural network (DNN). We compute the persistent homology of the activation data for each layer of the network and summarize this information using persistence landscapes. The resulting feature map provides both an informative visual- ization of the network and a kernel for statistical analysis and machine learning. We observe that the topological complexity often increases with training and that the topological complexity does not decrease with each layer.