Activation Landscapes as a Topological Summary of Neural Network Performance

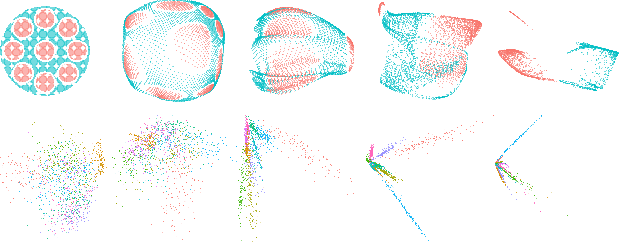
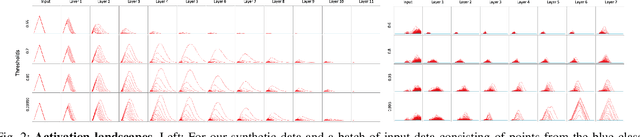
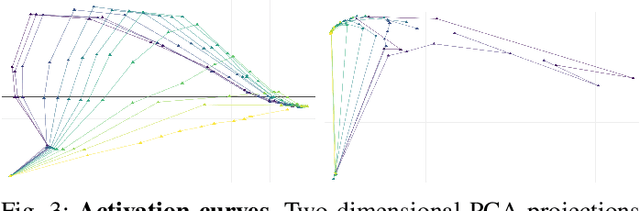
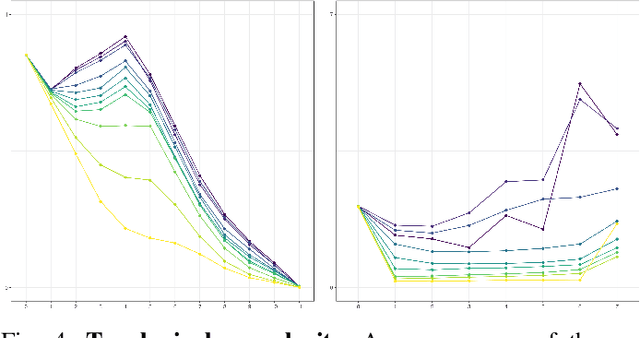
We use topological data analysis (TDA) to study how data transforms as it passes through successive layers of a deep neural network (DNN). We compute the persistent homology of the activation data for each layer of the network and summarize this information using persistence landscapes. The resulting feature map provides both an informative visual- ization of the network and a kernel for statistical analysis and machine learning. We observe that the topological complexity often increases with training and that the topological complexity does not decrease with each layer.

VolterraNet: A higher order convolutional network with group equivariance for homogeneous manifolds

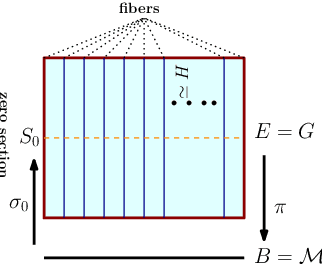
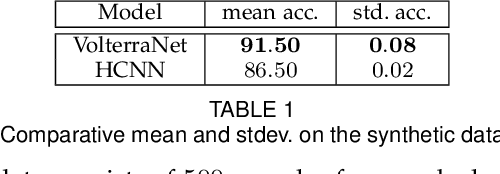
Convolutional neural networks have been highly successful in image-based learning tasks due to their translation equivariance property. Recent work has generalized the traditional convolutional layer of a convolutional neural network to non-Euclidean spaces and shown group equivariance of the generalized convolution operation. In this paper, we present a novel higher order Volterra convolutional neural network (VolterraNet) for data defined as samples of functions on Riemannian homogeneous spaces. Analagous to the result for traditional convolutions, we prove that the Volterra functional convolutions are equivariant to the action of the isometry group admitted by the Riemannian homogeneous spaces, and under some restrictions, any non-linear equivariant function can be expressed as our homogeneous space Volterra convolution, generalizing the non-linear shift equivariant characterization of Volterra expansions in Euclidean space. We also prove that second order functional convolution operations can be represented as cascaded convolutions which leads to an efficient implementation. Beyond this, we also propose a dilated VolterraNet model. These advances lead to large parameter reductions relative to baseline non-Euclidean CNNs. To demonstrate the efficacy of the VolterraNet performance, we present several real data experiments involving classification tasks on spherical-MNIST, atomic energy, Shrec17 data sets, and group testing on diffusion MRI data. Performance comparisons to the state-of-the-art are also presented.

ManifoldNet: A Deep Network Framework for Manifold-valued Data

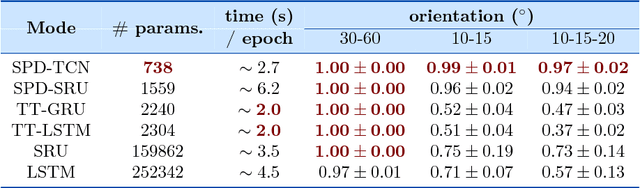
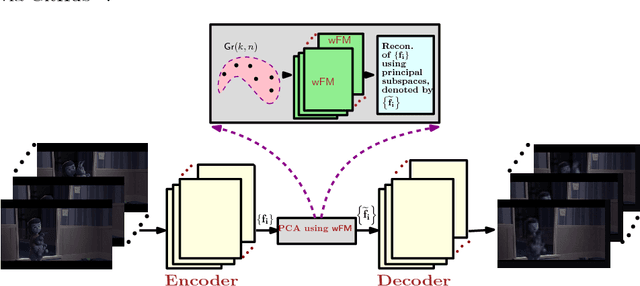
Deep neural networks have become the main work horse for many tasks involving learning from data in a variety of applications in Science and Engineering. Traditionally, the input to these networks lie in a vector space and the operations employed within the network are well defined on vector-spaces. In the recent past, due to technological advances in sensing, it has become possible to acquire manifold-valued data sets either directly or indirectly. Examples include but are not limited to data from omnidirectional cameras on automobiles, drones etc., synthetic aperture radar imaging, diffusion magnetic resonance imaging, elastography and conductance imaging in the Medical Imaging domain and others. Thus, there is need to generalize the deep neural networks to cope with input data that reside on curved manifolds where vector space operations are not naturally admissible. In this paper, we present a novel theoretical framework to generalize the widely popular convolutional neural networks (CNNs) to high dimensional manifold-valued data inputs. We call these networks, ManifoldNets. In ManifoldNets, convolution operation on data residing on Riemannian manifolds is achieved via a provably convergent recursive computation of the weighted Fr\'{e}chet Mean (wFM) of the given data, where the weights makeup the convolution mask, to be learned. Further, we prove that the proposed wFM layer achieves a contraction mapping and hence ManifoldNet does not need the non-linear ReLU unit used in standard CNNs. We present experiments, using the ManifoldNet framework, to achieve dimensionality reduction by computing the principal linear subspaces that naturally reside on a Grassmannian. The experimental results demonstrate the efficacy of ManifoldNets in the context of classification and reconstruction accuracy.