Baba C. Vemuri
A Steerable Deep Network for Model-Free Diffusion MRI Registration
Jan 10, 2025



Abstract:Nonrigid registration is vital to medical image analysis but remains challenging for diffusion MRI (dMRI) due to its high-dimensional, orientation-dependent nature. While classical methods are accurate, they are computationally demanding, and deep neural networks, though efficient, have been underexplored for nonrigid dMRI registration compared to structural imaging. We present a novel, deep learning framework for model-free, nonrigid registration of raw diffusion MRI data that does not require explicit reorientation. Unlike previous methods relying on derived representations such as diffusion tensors or fiber orientation distribution functions, in our approach, we formulate the registration as an equivariant diffeomorphism of position-and-orientation space. Central to our method is an $\mathsf{SE}(3)$-equivariant UNet that generates velocity fields while preserving the geometric properties of a raw dMRI's domain. We introduce a new loss function based on the maximum mean discrepancy in Fourier space, implicitly matching ensemble average propagators across images. Experimental results on Human Connectome Project dMRI data demonstrate competitive performance compared to state-of-the-art approaches, with the added advantage of bypassing the overhead for estimating derived representations. This work establishes a foundation for data-driven, geometry-aware dMRI registration directly in the acquisition space.
Higher Order Gauge Equivariant CNNs on Riemannian Manifolds and Applications
May 26, 2023



Abstract:With the advent of group equivariant convolutions in deep networks literature, spherical CNNs with $\mathsf{SO}(3)$-equivariant layers have been developed to cope with data that are samples of signals on the sphere $S^2$. One can implicitly obtain $\mathsf{SO}(3)$-equivariant convolutions on $S^2$ with significant efficiency gains by explicitly requiring gauge equivariance w.r.t. $\mathsf{SO}(2)$. In this paper, we build on this fact by introducing a higher order generalization of the gauge equivariant convolution, whose implementation is dubbed a gauge equivariant Volterra network (GEVNet). This allows us to model spatially extended nonlinear interactions within a given receptive field while still maintaining equivariance to global isometries. We prove theoretical results regarding the equivariance and construction of higher order gauge equivariant convolutions. Then, we empirically demonstrate the parameter efficiency of our model, first on computer vision benchmark data (e.g. spherical MNIST), and then in combination with a convolutional kernel network (CKN) on neuroimaging data. In the neuroimaging data experiments, the resulting two-part architecture (CKN + GEVNet) is used to automatically discriminate between patients with Lewy Body Disease (DLB), Alzheimer's Disease (AD) and Parkinson's Disease (PD) from diffusion magnetic resonance images (dMRI). The GEVNet extracts micro-architectural features within each voxel, while the CKN extracts macro-architectural features across voxels. This compound architecture is uniquely poised to exploit the intra- and inter-voxel information contained in the dMRI data, leading to improved performance over the classification results obtained from either of the individual components.
Horocycle Decision Boundaries for Large Margin Classification in Hyperbolic Space
Feb 14, 2023Abstract:Hyperbolic spaces have been quite popular in the recent past for representing hierarchically organized data. Further, several classification algorithms for data in these spaces have been proposed in the literature. These algorithms mainly use either hyperplanes or geodesics for decision boundaries in a large margin classifiers setting leading to a non-convex optimization problem. In this paper, we propose a novel large margin classifier based on horocycle (horosphere) decision boundaries that leads to a geodesically convex optimization problem that can be optimized using any Riemannian gradient descent technique guaranteeing a globally optimal solution. We present several experiments depicting the performance of our classifier.
Nested Hyperbolic Spaces for Dimensionality Reduction and Hyperbolic NN Design
Dec 03, 2021

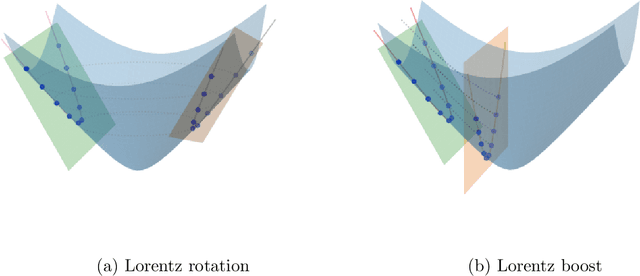

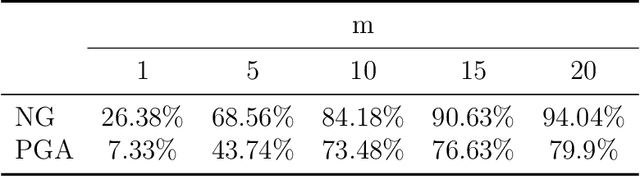
Abstract:Hyperbolic neural networks have been popular in the recent past due to their ability to represent hierarchical data sets effectively and efficiently. The challenge in developing these networks lies in the nonlinearity of the embedding space namely, the Hyperbolic space. Hyperbolic space is a homogeneous Riemannian manifold of the Lorentz group. Most existing methods (with some exceptions) use local linearization to define a variety of operations paralleling those used in traditional deep neural networks in Euclidean spaces. In this paper, we present a novel fully hyperbolic neural network which uses the concept of projections (embeddings) followed by an intrinsic aggregation and a nonlinearity all within the hyperbolic space. The novelty here lies in the projection which is designed to project data on to a lower-dimensional embedded hyperbolic space and hence leads to a nested hyperbolic space representation independently useful for dimensionality reduction. The main theoretical contribution is that the proposed embedding is proved to be isometric and equivariant under the Lorentz transformations. This projection is computationally efficient since it can be expressed by simple linear operations, and, due to the aforementioned equivariance property, it allows for weight sharing. The nested hyperbolic space representation is the core component of our network and therefore, we first compare this ensuing nested hyperbolic space representation with other dimensionality reduction methods such as tangent PCA, principal geodesic analysis (PGA) and HoroPCA. Based on this equivariant embedding, we develop a novel fully hyperbolic graph convolutional neural network architecture to learn the parameters of the projection. Finally, we present experiments demonstrating comparative performance of our network on several publicly available data sets.
VolterraNet: A higher order convolutional network with group equivariance for homogeneous manifolds
Jun 05, 2021
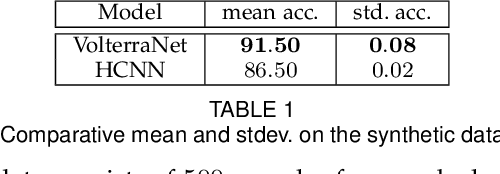


Abstract:Convolutional neural networks have been highly successful in image-based learning tasks due to their translation equivariance property. Recent work has generalized the traditional convolutional layer of a convolutional neural network to non-Euclidean spaces and shown group equivariance of the generalized convolution operation. In this paper, we present a novel higher order Volterra convolutional neural network (VolterraNet) for data defined as samples of functions on Riemannian homogeneous spaces. Analagous to the result for traditional convolutions, we prove that the Volterra functional convolutions are equivariant to the action of the isometry group admitted by the Riemannian homogeneous spaces, and under some restrictions, any non-linear equivariant function can be expressed as our homogeneous space Volterra convolution, generalizing the non-linear shift equivariant characterization of Volterra expansions in Euclidean space. We also prove that second order functional convolution operations can be represented as cascaded convolutions which leads to an efficient implementation. Beyond this, we also propose a dilated VolterraNet model. These advances lead to large parameter reductions relative to baseline non-Euclidean CNNs. To demonstrate the efficacy of the VolterraNet performance, we present several real data experiments involving classification tasks on spherical-MNIST, atomic energy, Shrec17 data sets, and group testing on diffusion MRI data. Performance comparisons to the state-of-the-art are also presented.
Nested Grassmanns for Dimensionality Reduction
Oct 27, 2020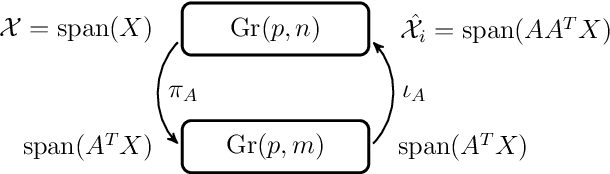

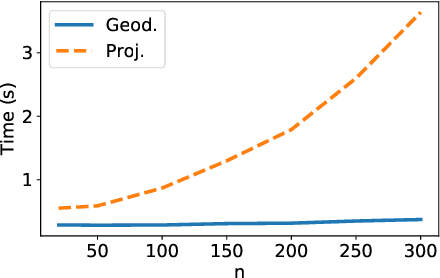
Abstract:Grassmann manifolds have been widely used to represent the geometry of feature spaces in a variety of problems in computer vision including but not limited to face recognition, action recognition, subspace clustering and motion segmentation. For these problems, the features usually lie in a very high-dimensional Grassmann manifold and hence an appropriate dimensionality reduction technique is called for in order to curtail the computational burden. To this end, the Principal Geodesic Analysis (PGA), a nonlinear extension of the well known principal component analysis, is applicable as a general tool to many Riemannian manifolds. In this paper, we propose a novel dimensionality reduction framework suited for Grassmann manifolds by utilizing the geometry of the manifold. Specifically, we project points in a Grassmann manifold to an embedded lower dimensional Grassmann manifold. A salient feature of our method is that it leads to higher expressed variance compared to PGA which we demonstrate via synthetic and real data experiments.
MVC-Net: A Convolutional Neural Network Architecture for Manifold-Valued Images With Applications
Mar 06, 2020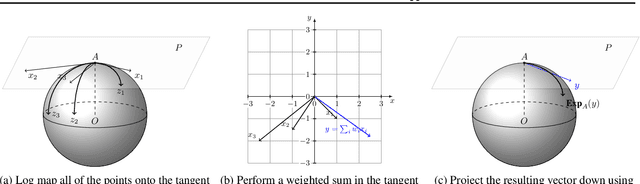


Abstract:Geometric deep learning has attracted significant attention in recent years, in part due to the availability of exotic data types for which traditional neural network architectures are not well suited. Our goal in this paper is to generalize convolutional neural networks (CNN) to the manifold-valued image case which arises commonly in medical imaging and computer vision applications. Explicitly, the input data to the network is an image where each pixel value is a sample from a Riemannian manifold. To achieve this goal, we must generalize the basic building block of traditional CNN architectures, namely, the weighted combinations operation. To this end, we develop a tangent space combination operation which is used to define a convolution operation on manifold-valued images that we call, the Manifold-Valued Convolution (MVC). We prove theoretical properties of the MVC operation, including equivariance to the action of the isometry group admitted by the manifold and characterizing when compositions of MVC layers collapse to a single layer. We present a detailed description of how to use MVC layers to build full, multi-layer neural networks that operate on manifold-valued images, which we call the MVC-net. Further, we empirically demonstrate superior performance of the MVC-nets in medical imaging and computer vision tasks.
A Statistical Recurrent Model on the Manifold of Symmetric Positive Definite Matrices
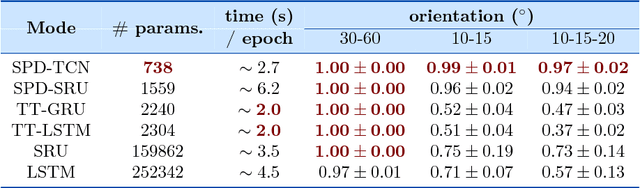
Oct 27, 2018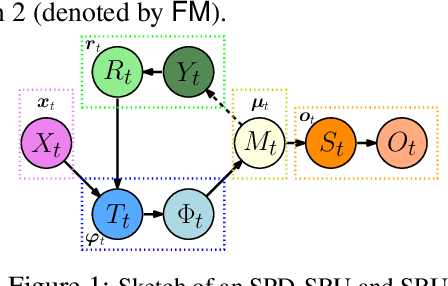
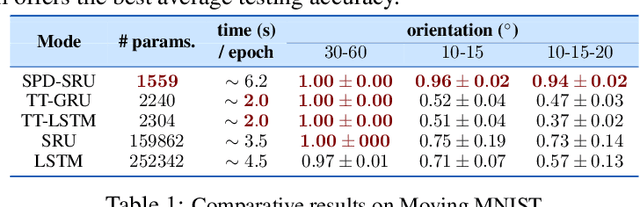
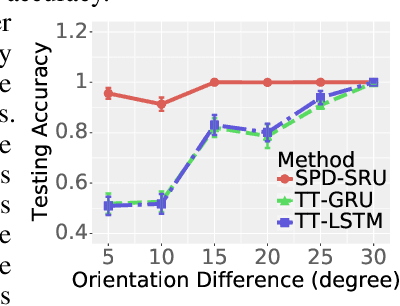
Abstract:In a number of disciplines, the data (e.g., graphs, manifolds) to be analyzed are non-Euclidean in nature. Geometric deep learning corresponds to techniques that generalize deep neural network models to such non-Euclidean spaces. Several recent papers have shown how convolutional neural networks (CNNs) can be extended to learn with graph-based data. In this work, we study the setting where the data (or measurements) are ordered, longitudinal or temporal in nature and live on a Riemannian manifold -- this setting is common in a variety of problems in statistical machine learning, vision and medical imaging. We show how recurrent statistical recurrent network models can be defined in such spaces. We give an efficient algorithm and conduct a rigorous analysis of its statistical properties. We perform extensive numerical experiments demonstrating competitive performance with state of the art methods but with significantly less number of parameters. We also show applications to a statistical analysis task in brain imaging, a regime where deep neural network models have only been utilized in limited ways.
ManifoldNet: A Deep Network Framework for Manifold-valued Data
Sep 20, 2018

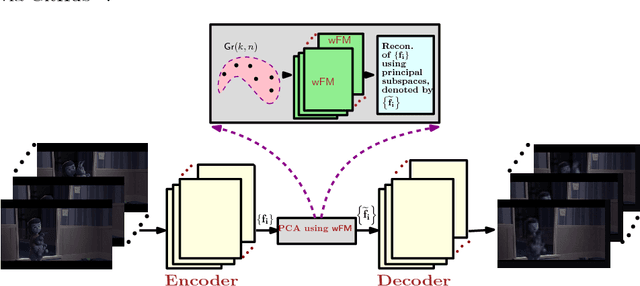
Abstract:Deep neural networks have become the main work horse for many tasks involving learning from data in a variety of applications in Science and Engineering. Traditionally, the input to these networks lie in a vector space and the operations employed within the network are well defined on vector-spaces. In the recent past, due to technological advances in sensing, it has become possible to acquire manifold-valued data sets either directly or indirectly. Examples include but are not limited to data from omnidirectional cameras on automobiles, drones etc., synthetic aperture radar imaging, diffusion magnetic resonance imaging, elastography and conductance imaging in the Medical Imaging domain and others. Thus, there is need to generalize the deep neural networks to cope with input data that reside on curved manifolds where vector space operations are not naturally admissible. In this paper, we present a novel theoretical framework to generalize the widely popular convolutional neural networks (CNNs) to high dimensional manifold-valued data inputs. We call these networks, ManifoldNets. In ManifoldNets, convolution operation on data residing on Riemannian manifolds is achieved via a provably convergent recursive computation of the weighted Fr\'{e}chet Mean (wFM) of the given data, where the weights makeup the convolution mask, to be learned. Further, we prove that the proposed wFM layer achieves a contraction mapping and hence ManifoldNet does not need the non-linear ReLU unit used in standard CNNs. We present experiments, using the ManifoldNet framework, to achieve dimensionality reduction by computing the principal linear subspaces that naturally reside on a Grassmannian. The experimental results demonstrate the efficacy of ManifoldNets in the context of classification and reconstruction accuracy.
A CNN for homogneous Riemannian manifolds with applications to Neuroimaging
Aug 06, 2018
Abstract:Convolutional neural networks are ubiquitous in Machine Learning applications for solving a variety of problems. They however can not be used in their native form when the domain of the data is commonly encountered manifolds such as the sphere, the special orthogonal group, the Grassmanian, the manifold of symmetric positive definite matrices and others. Most recently, generalization of CNNs to data domains such as the 2-sphere has been reported by some research groups, which is referred to as the spherical CNNs (SCNNs). The key property of SCNNs distinct from CNNs is that they exhibit the rotational equivariance property that allows for sharing learned weights within a layer. In this paper, we theoretically generalize the CNNs to Riemannian homogeneous manifolds, that include but are not limited to the aforementioned example manifolds. Our key contributions in this work are: (i) A theorem stating that linear group equivariance systems are fully characterized by correlation of functions on the domain manifold and vice-versa. This is fundamental to the characterization of all linear group equivariant systems and parallels the widely used result in linear system theory for vector spaces. (ii) As a corrolary, we prove the equivariance of the correlation operation to group actions admitted by the input domains which are Riemannian homogeneous manifolds. (iii) We present the first end-to-end deep network architecture for classification of diffusion magnetic resonance image (dMRI) scans acquired from a cohort of 44 Parkinson Disease patients and 50 control/normal subjects. (iv) A proof of concept experiment involving synthetic data generated on the manifold of symmetric positive definite matrices is presented to demonstrate the applicability of our network to other types of domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge