Field-of-View Extension for Diffusion MRI via Deep Generative Models

Purpose: In diffusion MRI (dMRI), the volumetric and bundle analyses of whole-brain tissue microstructure and connectivity can be severely impeded by an incomplete field-of-view (FOV). This work aims to develop a method for imputing the missing slices directly from existing dMRI scans with an incomplete FOV. We hypothesize that the imputed image with complete FOV can improve the whole-brain tractography for corrupted data with incomplete FOV. Therefore, our approach provides a desirable alternative to discarding the valuable dMRI data, enabling subsequent tractography analyses that would otherwise be challenging or unattainable with corrupted data. Approach: We propose a framework based on a deep generative model that estimates the absent brain regions in dMRI scans with incomplete FOV. The model is capable of learning both the diffusion characteristics in diffusion-weighted images (DWI) and the anatomical features evident in the corresponding structural images for efficiently imputing missing slices of DWI outside of incomplete FOV. Results: For evaluating the imputed slices, on the WRAP dataset the proposed framework achieved PSNRb0=22.397, SSIMb0=0.905, PSNRb1300=22.479, SSIMb1300=0.893; on the NACC dataset it achieved PSNRb0=21.304, SSIMb0=0.892, PSNRb1300=21.599, SSIMb1300= 0.877. The proposed framework improved the tractography accuracy, as demonstrated by an increased average Dice score for 72 tracts (p < 0.001) on both the WRAP and NACC datasets. Conclusions: Results suggest that the proposed framework achieved sufficient imputation performance in dMRI data with incomplete FOV for improving whole-brain tractography, thereby repairing the corrupted data. Our approach achieved more accurate whole-brain tractography results with extended and complete FOV and reduced the uncertainty when analyzing bundles associated with Alzheimer's Disease.

Evaluation of Mean Shift, ComBat, and CycleGAN for Harmonizing Brain Connectivity Matrices Across Sites

Connectivity matrices derived from diffusion MRI (dMRI) provide an interpretable and generalizable way of understanding the human brain connectome. However, dMRI suffers from inter-site and between-scanner variation, which impedes analysis across datasets to improve robustness and reproducibility of results. To evaluate different harmonization approaches on connectivity matrices, we compared graph measures derived from these matrices before and after applying three harmonization techniques: mean shift, ComBat, and CycleGAN. The sample comprises 168 age-matched, sex-matched normal subjects from two studies: the Vanderbilt Memory and Aging Project (VMAP) and the Biomarkers of Cognitive Decline Among Normal Individuals (BIOCARD). First, we plotted the graph measures and used coefficient of variation (CoV) and the Mann-Whitney U test to evaluate different methods' effectiveness in removing site effects on the matrices and the derived graph measures. ComBat effectively eliminated site effects for global efficiency and modularity and outperformed the other two methods. However, all methods exhibited poor performance when harmonizing average betweenness centrality. Second, we tested whether our harmonization methods preserved correlations between age and graph measures. All methods except for CycleGAN in one direction improved correlations between age and global efficiency and between age and modularity from insignificant to significant with p-values less than 0.05.

A Statistical Recurrent Model on the Manifold of Symmetric Positive Definite Matrices

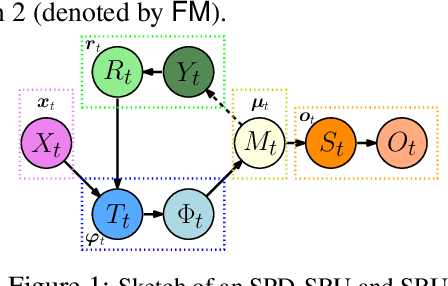
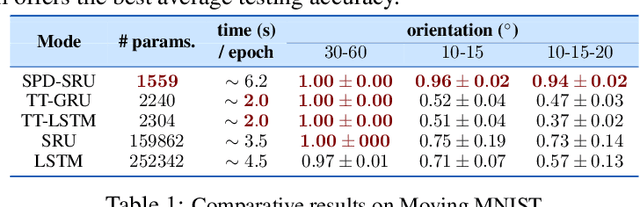
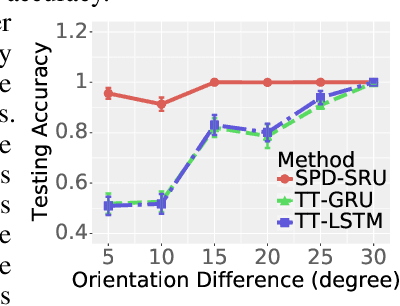
In a number of disciplines, the data (e.g., graphs, manifolds) to be analyzed are non-Euclidean in nature. Geometric deep learning corresponds to techniques that generalize deep neural network models to such non-Euclidean spaces. Several recent papers have shown how convolutional neural networks (CNNs) can be extended to learn with graph-based data. In this work, we study the setting where the data (or measurements) are ordered, longitudinal or temporal in nature and live on a Riemannian manifold -- this setting is common in a variety of problems in statistical machine learning, vision and medical imaging. We show how recurrent statistical recurrent network models can be defined in such spaces. We give an efficient algorithm and conduct a rigorous analysis of its statistical properties. We perform extensive numerical experiments demonstrating competitive performance with state of the art methods but with significantly less number of parameters. We also show applications to a statistical analysis task in brain imaging, a regime where deep neural network models have only been utilized in limited ways.