Higher Order Gauge Equivariant CNNs on Riemannian Manifolds and Applications

With the advent of group equivariant convolutions in deep networks literature, spherical CNNs with $\mathsf{SO}(3)$-equivariant layers have been developed to cope with data that are samples of signals on the sphere $S^2$. One can implicitly obtain $\mathsf{SO}(3)$-equivariant convolutions on $S^2$ with significant efficiency gains by explicitly requiring gauge equivariance w.r.t. $\mathsf{SO}(2)$. In this paper, we build on this fact by introducing a higher order generalization of the gauge equivariant convolution, whose implementation is dubbed a gauge equivariant Volterra network (GEVNet). This allows us to model spatially extended nonlinear interactions within a given receptive field while still maintaining equivariance to global isometries. We prove theoretical results regarding the equivariance and construction of higher order gauge equivariant convolutions. Then, we empirically demonstrate the parameter efficiency of our model, first on computer vision benchmark data (e.g. spherical MNIST), and then in combination with a convolutional kernel network (CKN) on neuroimaging data. In the neuroimaging data experiments, the resulting two-part architecture (CKN + GEVNet) is used to automatically discriminate between patients with Lewy Body Disease (DLB), Alzheimer's Disease (AD) and Parkinson's Disease (PD) from diffusion magnetic resonance images (dMRI). The GEVNet extracts micro-architectural features within each voxel, while the CKN extracts macro-architectural features across voxels. This compound architecture is uniquely poised to exploit the intra- and inter-voxel information contained in the dMRI data, leading to improved performance over the classification results obtained from either of the individual components.

MVC-Net: A Convolutional Neural Network Architecture for Manifold-Valued Images With Applications

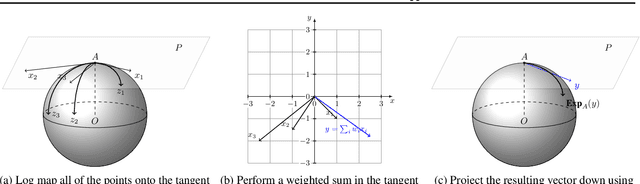
Geometric deep learning has attracted significant attention in recent years, in part due to the availability of exotic data types for which traditional neural network architectures are not well suited. Our goal in this paper is to generalize convolutional neural networks (CNN) to the manifold-valued image case which arises commonly in medical imaging and computer vision applications. Explicitly, the input data to the network is an image where each pixel value is a sample from a Riemannian manifold. To achieve this goal, we must generalize the basic building block of traditional CNN architectures, namely, the weighted combinations operation. To this end, we develop a tangent space combination operation which is used to define a convolution operation on manifold-valued images that we call, the Manifold-Valued Convolution (MVC). We prove theoretical properties of the MVC operation, including equivariance to the action of the isometry group admitted by the manifold and characterizing when compositions of MVC layers collapse to a single layer. We present a detailed description of how to use MVC layers to build full, multi-layer neural networks that operate on manifold-valued images, which we call the MVC-net. Further, we empirically demonstrate superior performance of the MVC-nets in medical imaging and computer vision tasks.

A Statistical Recurrent Model on the Manifold of Symmetric Positive Definite Matrices

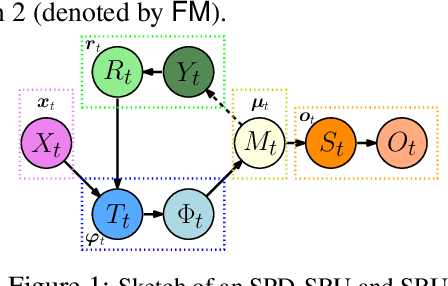
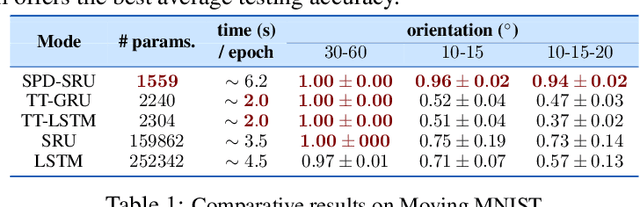
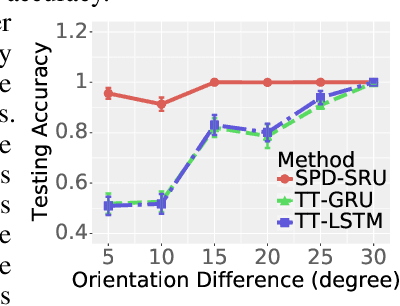
In a number of disciplines, the data (e.g., graphs, manifolds) to be analyzed are non-Euclidean in nature. Geometric deep learning corresponds to techniques that generalize deep neural network models to such non-Euclidean spaces. Several recent papers have shown how convolutional neural networks (CNNs) can be extended to learn with graph-based data. In this work, we study the setting where the data (or measurements) are ordered, longitudinal or temporal in nature and live on a Riemannian manifold -- this setting is common in a variety of problems in statistical machine learning, vision and medical imaging. We show how recurrent statistical recurrent network models can be defined in such spaces. We give an efficient algorithm and conduct a rigorous analysis of its statistical properties. We perform extensive numerical experiments demonstrating competitive performance with state of the art methods but with significantly less number of parameters. We also show applications to a statistical analysis task in brain imaging, a regime where deep neural network models have only been utilized in limited ways.