Variational Sampling of Temporal Trajectories

A deterministic temporal process can be determined by its trajectory, an element in the product space of (a) initial condition $z_0 \in \mathcal{Z}$ and (b) transition function $f: (\mathcal{Z}, \mathcal{T}) \to \mathcal{Z}$ often influenced by the control of the underlying dynamical system. Existing methods often model the transition function as a differential equation or as a recurrent neural network. Despite their effectiveness in predicting future measurements, few results have successfully established a method for sampling and statistical inference of trajectories using neural networks, partially due to constraints in the parameterization. In this work, we introduce a mechanism to learn the distribution of trajectories by parameterizing the transition function $f$ explicitly as an element in a function space. Our framework allows efficient synthesis of novel trajectories, while also directly providing a convenient tool for inference, i.e., uncertainty estimation, likelihood evaluations and out of distribution detection for abnormal trajectories. These capabilities can have implications for various downstream tasks, e.g., simulation and evaluation for reinforcement learning.

On the Versatile Uses of Partial Distance Correlation in Deep Learning

Comparing the functional behavior of neural network models, whether it is a single network over time or two (or more networks) during or post-training, is an essential step in understanding what they are learning (and what they are not), and for identifying strategies for regularization or efficiency improvements. Despite recent progress, e.g., comparing vision transformers to CNNs, systematic comparison of function, especially across different networks, remains difficult and is often carried out layer by layer. Approaches such as canonical correlation analysis (CCA) are applicable in principle, but have been sparingly used so far. In this paper, we revisit a (less widely known) from statistics, called distance correlation (and its partial variant), designed to evaluate correlation between feature spaces of different dimensions. We describe the steps necessary to carry out its deployment for large scale models -- this opens the door to a surprising array of applications ranging from conditioning one deep model w.r.t. another, learning disentangled representations as well as optimizing diverse models that would directly be more robust to adversarial attacks. Our experiments suggest a versatile regularizer (or constraint) with many advantages, which avoids some of the common difficulties one faces in such analyses. Code is at https://github.com/zhenxingjian/Partial_Distance_Correlation.

Equivariance Allows Handling Multiple Nuisance Variables When Analyzing Pooled Neuroimaging Datasets

Pooling multiple neuroimaging datasets across institutions often enables improvements in statistical power when evaluating associations (e.g., between risk factors and disease outcomes) that may otherwise be too weak to detect. When there is only a {\em single} source of variability (e.g., different scanners), domain adaptation and matching the distributions of representations may suffice in many scenarios. But in the presence of {\em more than one} nuisance variable which concurrently influence the measurements, pooling datasets poses unique challenges, e.g., variations in the data can come from both the acquisition method as well as the demographics of participants (gender, age). Invariant representation learning, by itself, is ill-suited to fully model the data generation process. In this paper, we show how bringing recent results on equivariant representation learning (for studying symmetries in neural networks) instantiated on structured spaces together with simple use of classical results on causal inference provides an effective practical solution. In particular, we demonstrate how our model allows dealing with more than one nuisance variable under some assumptions and can enable analysis of pooled scientific datasets in scenarios that would otherwise entail removing a large portion of the samples.

Mixed Effects Neural ODE: A Variational Approximation for Analyzing the Dynamics of Panel Data

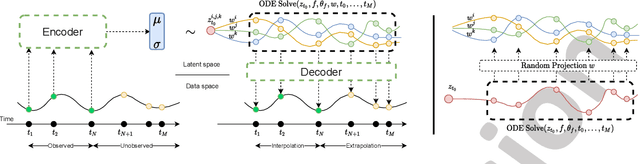
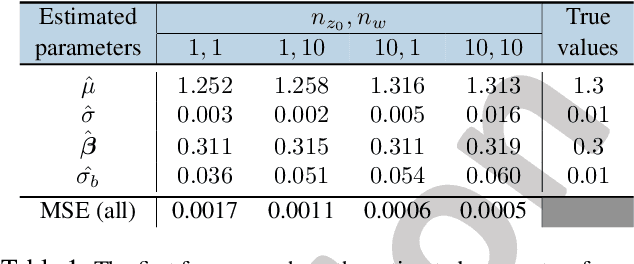
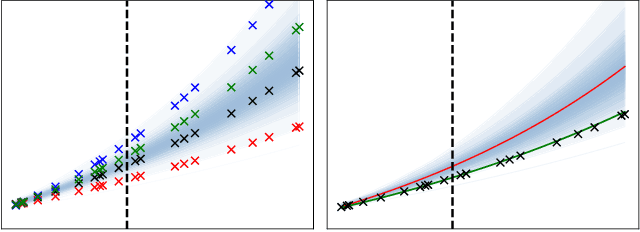
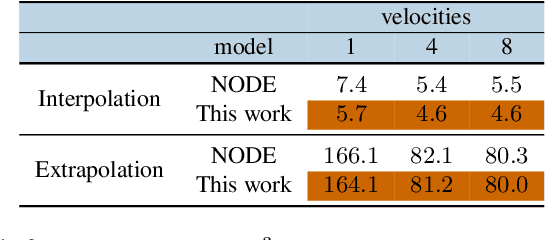
Panel data involving longitudinal measurements of the same set of participants taken over multiple time points is common in studies to understand childhood development and disease modeling. Deep hybrid models that marry the predictive power of neural networks with physical simulators such as differential equations, are starting to drive advances in such applications. The task of modeling not just the observations but the hidden dynamics that are captured by the measurements poses interesting statistical/computational questions. We propose a probabilistic model called ME-NODE to incorporate (fixed + random) mixed effects for analyzing such panel data. We show that our model can be derived using smooth approximations of SDEs provided by the Wong-Zakai theorem. We then derive Evidence Based Lower Bounds for ME-NODE, and develop (efficient) training algorithms using MC based sampling methods and numerical ODE solvers. We demonstrate ME-NODE's utility on tasks spanning the spectrum from simulations and toy data to real longitudinal 3D imaging data from an Alzheimer's disease (AD) study, and study its performance in terms of accuracy of reconstruction for interpolation, uncertainty estimates and personalized prediction.

Forward Operator Estimation in Generative Models with Kernel Transfer Operators

Generative models which use explicit density modeling (e.g., variational autoencoders, flow-based generative models) involve finding a mapping from a known distribution, e.g. Gaussian, to the unknown input distribution. This often requires searching over a class of non-linear functions (e.g., representable by a deep neural network). While effective in practice, the associated runtime/memory costs can increase rapidly, usually as a function of the performance desired in an application. We propose a much cheaper (and simpler) strategy to estimate this mapping based on adapting known results in kernel transfer operators. We show that our formulation enables highly efficient distribution approximation and sampling, and offers surprisingly good empirical performance that compares favorably with powerful baselines, but with significant runtime savings. We show that the algorithm also performs well in small sample size settings (in brain imaging).

An Online Riemannian PCA for Stochastic Canonical Correlation Analysis

We present an efficient stochastic algorithm (RSG+) for canonical correlation analysis (CCA) using a reparametrization of the projection matrices. We show how this reparametrization (into structured matrices), simple in hindsight, directly presents an opportunity to repurpose/adjust mature techniques for numerical optimization on Riemannian manifolds. Our developments nicely complement existing methods for this problem which either require $O(d^3)$ time complexity per iteration with $O(\frac{1}{\sqrt{t}})$ convergence rate (where $d$ is the dimensionality) or only extract the top $1$ component with $O(\frac{1}{t})$ convergence rate. In contrast, our algorithm offers a strict improvement for this classical problem: it achieves $O(d^2k)$ runtime complexity per iteration for extracting the top $k$ canonical components with $O(\frac{1}{t})$ convergence rate. While the paper primarily focuses on the formulation and technical analysis of its properties, our experiments show that the empirical behavior on common datasets is quite promising. We also explore a potential application in training fair models where the label of protected attribute is missing or otherwise unavailable.

VolterraNet: A higher order convolutional network with group equivariance for homogeneous manifolds

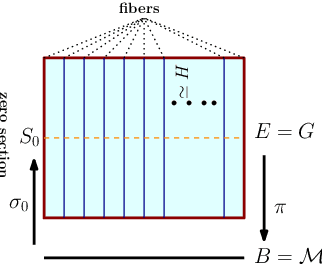
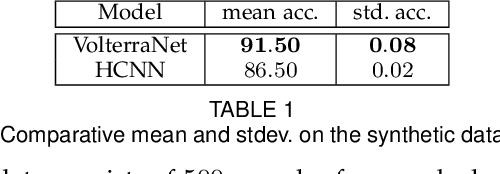
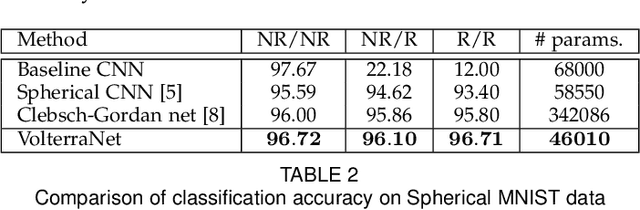
Convolutional neural networks have been highly successful in image-based learning tasks due to their translation equivariance property. Recent work has generalized the traditional convolutional layer of a convolutional neural network to non-Euclidean spaces and shown group equivariance of the generalized convolution operation. In this paper, we present a novel higher order Volterra convolutional neural network (VolterraNet) for data defined as samples of functions on Riemannian homogeneous spaces. Analagous to the result for traditional convolutions, we prove that the Volterra functional convolutions are equivariant to the action of the isometry group admitted by the Riemannian homogeneous spaces, and under some restrictions, any non-linear equivariant function can be expressed as our homogeneous space Volterra convolution, generalizing the non-linear shift equivariant characterization of Volterra expansions in Euclidean space. We also prove that second order functional convolution operations can be represented as cascaded convolutions which leads to an efficient implementation. Beyond this, we also propose a dilated VolterraNet model. These advances lead to large parameter reductions relative to baseline non-Euclidean CNNs. To demonstrate the efficacy of the VolterraNet performance, we present several real data experiments involving classification tasks on spherical-MNIST, atomic energy, Shrec17 data sets, and group testing on diffusion MRI data. Performance comparisons to the state-of-the-art are also presented.

Simpler Certified Radius Maximization by Propagating Covariances

One strategy for adversarially training a robust model is to maximize its certified radius -- the neighborhood around a given training sample for which the model's prediction remains unchanged. The scheme typically involves analyzing a "smoothed" classifier where one estimates the prediction corresponding to Gaussian samples in the neighborhood of each sample in the mini-batch, accomplished in practice by Monte Carlo sampling. In this paper, we investigate the hypothesis that this sampling bottleneck can potentially be mitigated by identifying ways to directly propagate the covariance matrix of the smoothed distribution through the network. To this end, we find that other than certain adjustments to the network, propagating the covariances must also be accompanied by additional accounting that keeps track of how the distributional moments transform and interact at each stage in the network. We show how satisfying these criteria yields an algorithm for maximizing the certified radius on datasets including Cifar-10, ImageNet, and Places365 while offering runtime savings on networks with moderate depth, with a small compromise in overall accuracy. We describe the details of the key modifications that enable practical use. Via various experiments, we evaluate when our simplifications are sensible, and what the key benefits and limitations are.

Nyströmformer: A Nyström-Based Algorithm for Approximating Self-Attention

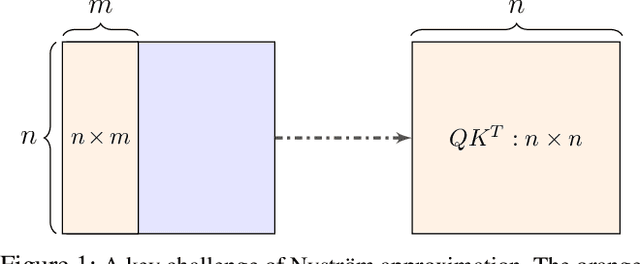
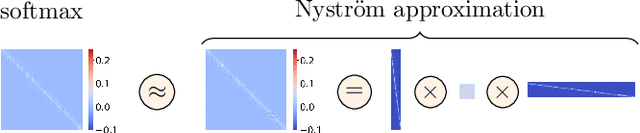
Transformers have emerged as a powerful tool for a broad range of natural language processing tasks. A key component that drives the impressive performance of Transformers is the self-attention mechanism that encodes the influence or dependence of other tokens on each specific token. While beneficial, the quadratic complexity of self-attention on the input sequence length has limited its application to longer sequences -- a topic being actively studied in the community. To address this limitation, we propose Nystr\"{o}mformer -- a model that exhibits favorable scalability as a function of sequence length. Our idea is based on adapting the Nystr\"{o}m method to approximate standard self-attention with $O(n)$ complexity. The scalability of Nystr\"{o}mformer enables application to longer sequences with thousands of tokens. We perform evaluations on multiple downstream tasks on the GLUE benchmark and IMDB reviews with standard sequence length, and find that our Nystr\"{o}mformer performs comparably, or in a few cases, even slightly better, than standard self-attention. On longer sequence tasks in the Long Range Arena (LRA) benchmark, Nystr\"{o}mformer performs favorably relative to other efficient self-attention methods. Our code is available at https://github.com/mlpen/Nystromformer.

Flow-based Generative Models for Learning Manifold to Manifold Mappings

Many measurements or observations in computer vision and machine learning manifest as non-Euclidean data. While recent proposals (like spherical CNN) have extended a number of deep neural network architectures to manifold-valued data, and this has often provided strong improvements in performance, the literature on generative models for manifold data is quite sparse. Partly due to this gap, there are also no modality transfer/translation models for manifold-valued data whereas numerous such methods based on generative models are available for natural images. This paper addresses this gap, motivated by a need in brain imaging -- in doing so, we expand the operating range of certain generative models (as well as generative models for modality transfer) from natural images to images with manifold-valued measurements. Our main result is the design of a two-stream version of GLOW (flow-based invertible generative models) that can synthesize information of a field of one type of manifold-valued measurements given another. On the theoretical side, we introduce three kinds of invertible layers for manifold-valued data, which are not only analogous to their functionality in flow-based generative models (e.g., GLOW) but also preserve the key benefits (determinants of the Jacobian are easy to calculate). For experiments, on a large dataset from the Human Connectome Project (HCP), we show promising results where we can reliably and accurately reconstruct brain images of a field of orientation distribution functions (ODF) from diffusion tensor images (DTI), where the latter has a $5\times$ faster acquisition time but at the expense of worse angular resolution.