Variational Sampling of Temporal Trajectories

A deterministic temporal process can be determined by its trajectory, an element in the product space of (a) initial condition $z_0 \in \mathcal{Z}$ and (b) transition function $f: (\mathcal{Z}, \mathcal{T}) \to \mathcal{Z}$ often influenced by the control of the underlying dynamical system. Existing methods often model the transition function as a differential equation or as a recurrent neural network. Despite their effectiveness in predicting future measurements, few results have successfully established a method for sampling and statistical inference of trajectories using neural networks, partially due to constraints in the parameterization. In this work, we introduce a mechanism to learn the distribution of trajectories by parameterizing the transition function $f$ explicitly as an element in a function space. Our framework allows efficient synthesis of novel trajectories, while also directly providing a convenient tool for inference, i.e., uncertainty estimation, likelihood evaluations and out of distribution detection for abnormal trajectories. These capabilities can have implications for various downstream tasks, e.g., simulation and evaluation for reinforcement learning.

Using Intermediate Forward Iterates for Intermediate Generator Optimization

Score-based models have recently been introduced as a richer framework to model distributions in high dimensions and are generally more suitable for generative tasks. In score-based models, a generative task is formulated using a parametric model (such as a neural network) to directly learn the gradient of such high dimensional distributions, instead of the density functions themselves, as is done traditionally. From the mathematical point of view, such gradient information can be utilized in reverse by stochastic sampling to generate diverse samples. However, from a computational perspective, existing score-based models can be efficiently trained only if the forward or the corruption process can be computed in closed form. By using the relationship between the process and layers in a feed-forward network, we derive a backpropagation-based procedure which we call Intermediate Generator Optimization to utilize intermediate iterates of the process with negligible computational overhead. The main advantage of IGO is that it can be incorporated into any standard autoencoder pipeline for the generative task. We analyze the sample complexity properties of IGO to solve downstream tasks like Generative PCA. We show applications of the IGO on two dense predictive tasks viz., image extrapolation, and point cloud denoising. Our experiments indicate that obtaining an ensemble of generators for various time points is possible using first-order methods.

Radial Spike and Slab Bayesian Neural Networks for Sparse Data in Ransomware Attacks

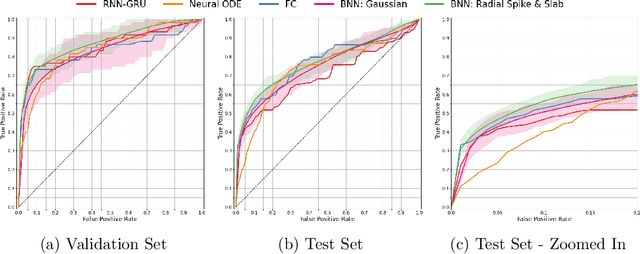
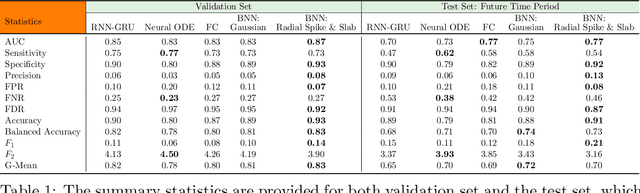
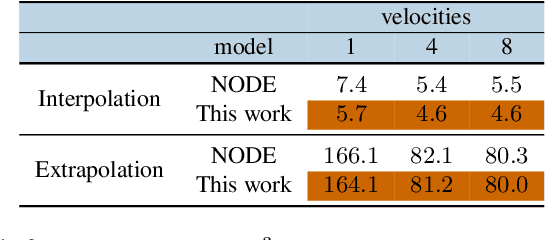
Ransomware attacks are increasing at an alarming rate, leading to large financial losses, unrecoverable encrypted data, data leakage, and privacy concerns. The prompt detection of ransomware attacks is required to minimize further damage, particularly during the encryption stage. However, the frequency and structure of the observed ransomware attack data makes this task difficult to accomplish in practice. The data corresponding to ransomware attacks represents temporal, high-dimensional sparse signals, with limited records and very imbalanced classes. While traditional deep learning models have been able to achieve state-of-the-art results in a wide variety of domains, Bayesian Neural Networks, which are a class of probabilistic models, are better suited to the issues of the ransomware data. These models combine ideas from Bayesian statistics with the rich expressive power of neural networks. In this paper, we propose the Radial Spike and Slab Bayesian Neural Network, which is a new type of Bayesian Neural network that includes a new form of the approximate posterior distribution. The model scales well to large architectures and recovers the sparse structure of target functions. We provide a theoretical justification for using this type of distribution, as well as a computationally efficient method to perform variational inference. We demonstrate the performance of our model on a real dataset of ransomware attacks and show improvement over a large number of baselines, including state-of-the-art models such as Neural ODEs (ordinary differential equations). In addition, we propose to represent low-level events as MITRE ATT\&CK tactics, techniques, and procedures (TTPs) which allows the model to better generalize to unseen ransomware attacks.

Image2Gif: Generating Continuous Realistic Animations with Warping NODEs

Generating smooth animations from a limited number of sequential observations has a number of applications in vision. For example, it can be used to increase number of frames per second, or generating a new trajectory only based on first and last frames, e.g. a motion of face emotions. Despite the discrete observed data (frames), the problem of generating a new trajectory is a continues problem. In addition, to be perceptually realistic, the domain of an image should not alter drastically through the trajectory of changes. In this paper, we propose a new framework, Warping Neural ODE, for generating a smooth animation (video frame interpolation) in a continuous manner, given two ("farther apart") frames, denoting the start and the end of the animation. The key feature of our framework is utilizing the continuous spatial transformation of the image based on the vector field, derived from a system of differential equations. This allows us to achieve the smoothness and the realism of an animation with infinitely small time steps between the frames. We show the application of our work in generating an animation given two frames, in different training settings, including Generative Adversarial Network (GAN) and with $L_2$ loss.

Graph Reparameterizations for Enabling 1000+ Monte Carlo Iterations in Bayesian Deep Neural Networks

Uncertainty estimation in deep models is essential in many real-world applications and has benefited from developments over the last several years. Recent evidence suggests that existing solutions dependent on simple Gaussian formulations may not be sufficient. However, moving to other distributions necessitates Monte Carlo (MC) sampling to estimate quantities such as the KL divergence: it could be expensive and scales poorly as the dimensions of both the input data and the model grow. This is directly related to the structure of the computation graph, which can grow linearly as a function of the number of MC samples needed. Here, we construct a framework to describe these computation graphs, and identify probability families where the graph size can be independent or only weakly dependent on the number of MC samples. These families correspond directly to large classes of distributions. Empirically, we can run a much larger number of iterations for MC approximations for larger architectures used in computer vision with gains in performance measured in confident accuracy, stability of training, memory and training time.

Mixed Effects Neural ODE: A Variational Approximation for Analyzing the Dynamics of Panel Data

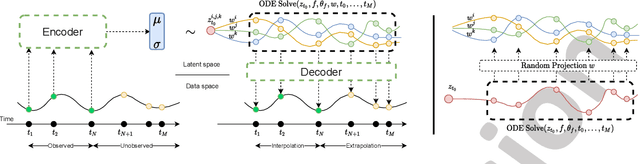
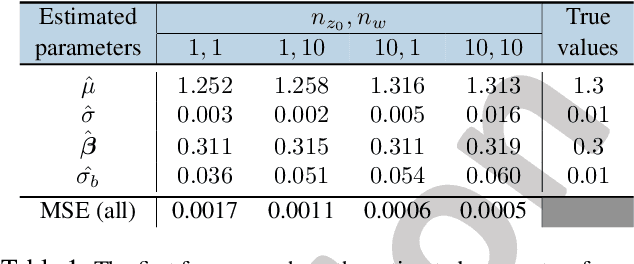
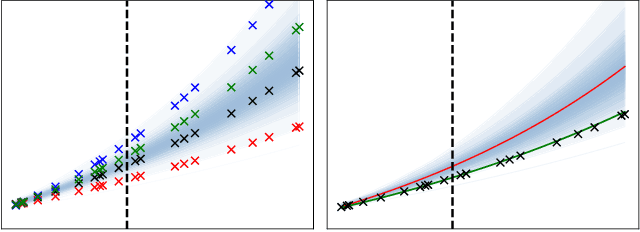
Panel data involving longitudinal measurements of the same set of participants taken over multiple time points is common in studies to understand childhood development and disease modeling. Deep hybrid models that marry the predictive power of neural networks with physical simulators such as differential equations, are starting to drive advances in such applications. The task of modeling not just the observations but the hidden dynamics that are captured by the measurements poses interesting statistical/computational questions. We propose a probabilistic model called ME-NODE to incorporate (fixed + random) mixed effects for analyzing such panel data. We show that our model can be derived using smooth approximations of SDEs provided by the Wong-Zakai theorem. We then derive Evidence Based Lower Bounds for ME-NODE, and develop (efficient) training algorithms using MC based sampling methods and numerical ODE solvers. We demonstrate ME-NODE's utility on tasks spanning the spectrum from simulations and toy data to real longitudinal 3D imaging data from an Alzheimer's disease (AD) study, and study its performance in terms of accuracy of reconstruction for interpolation, uncertainty estimates and personalized prediction.

Ordinal-Quadruplet: Retrieval of Missing Classes in Ordinal Time Series

In this paper, we propose an ordered time series classification framework that is robust against missing classes in the training data, i.e., during testing we can prescribe classes that are missing during training. This framework relies on two main components: (1) our newly proposed ordinal-quadruplet loss, which forces the model to learn latent representation while preserving the ordinal relation among labels, (2) testing procedure, which utilizes the property of latent representation (order preservation). We conduct experiments based on real world multivariate time series data and show the significant improvement in the prediction of missing labels even with 40% of the classes are missing from training. Compared with the well-known triplet loss optimization augmented with interpolation for missing information, in some cases, we nearly double the accuracy.