Mixed Effects Neural ODE: A Variational Approximation for Analyzing the Dynamics of Panel Data

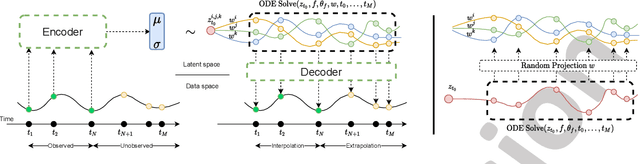
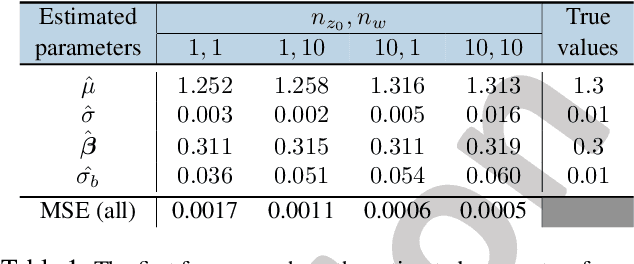
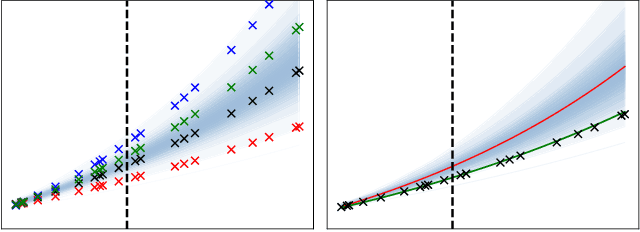
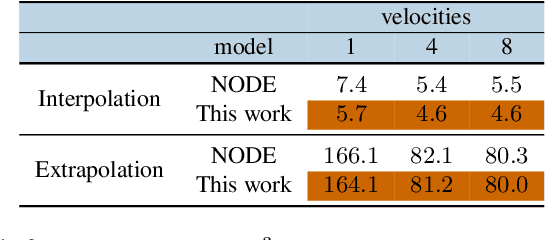
Panel data involving longitudinal measurements of the same set of participants taken over multiple time points is common in studies to understand childhood development and disease modeling. Deep hybrid models that marry the predictive power of neural networks with physical simulators such as differential equations, are starting to drive advances in such applications. The task of modeling not just the observations but the hidden dynamics that are captured by the measurements poses interesting statistical/computational questions. We propose a probabilistic model called ME-NODE to incorporate (fixed + random) mixed effects for analyzing such panel data. We show that our model can be derived using smooth approximations of SDEs provided by the Wong-Zakai theorem. We then derive Evidence Based Lower Bounds for ME-NODE, and develop (efficient) training algorithms using MC based sampling methods and numerical ODE solvers. We demonstrate ME-NODE's utility on tasks spanning the spectrum from simulations and toy data to real longitudinal 3D imaging data from an Alzheimer's disease (AD) study, and study its performance in terms of accuracy of reconstruction for interpolation, uncertainty estimates and personalized prediction.

Generating Accurate Pseudo-labels via Hermite Polynomials for SSL Confidently

Rectified Linear Units (ReLUs) are among the most widely used activation function in a broad variety of tasks in vision. Recent theoretical results suggest that despite their excellent practical performance, in various cases, a substitution with basis expansions (e.g., polynomials) can yield significant benefits from both the optimization and generalization perspective. Unfortunately, the existing results remain limited to networks with a couple of layers, and the practical viability of these results is not yet known. Motivated by some of these results, we explore the use of Hermite polynomial expansions as a substitute for ReLUs in deep networks. While our experiments with supervised learning do not provide a clear verdict, we find that this strategy offers considerable benefits in semi-supervised learning (SSL) / transductive learning settings. We carefully develop this idea and show how the use of Hermite polynomials based activations can yield improvements in pseudo-label accuracies and sizable financial savings (due to concurrent runtime benefits). Further, we show via theoretical analysis, that the networks (with Hermite activations) offer robustness to noise and other attractive mathematical properties.