Variational Sampling of Temporal Trajectories

A deterministic temporal process can be determined by its trajectory, an element in the product space of (a) initial condition $z_0 \in \mathcal{Z}$ and (b) transition function $f: (\mathcal{Z}, \mathcal{T}) \to \mathcal{Z}$ often influenced by the control of the underlying dynamical system. Existing methods often model the transition function as a differential equation or as a recurrent neural network. Despite their effectiveness in predicting future measurements, few results have successfully established a method for sampling and statistical inference of trajectories using neural networks, partially due to constraints in the parameterization. In this work, we introduce a mechanism to learn the distribution of trajectories by parameterizing the transition function $f$ explicitly as an element in a function space. Our framework allows efficient synthesis of novel trajectories, while also directly providing a convenient tool for inference, i.e., uncertainty estimation, likelihood evaluations and out of distribution detection for abnormal trajectories. These capabilities can have implications for various downstream tasks, e.g., simulation and evaluation for reinforcement learning.

On the Versatile Uses of Partial Distance Correlation in Deep Learning

Comparing the functional behavior of neural network models, whether it is a single network over time or two (or more networks) during or post-training, is an essential step in understanding what they are learning (and what they are not), and for identifying strategies for regularization or efficiency improvements. Despite recent progress, e.g., comparing vision transformers to CNNs, systematic comparison of function, especially across different networks, remains difficult and is often carried out layer by layer. Approaches such as canonical correlation analysis (CCA) are applicable in principle, but have been sparingly used so far. In this paper, we revisit a (less widely known) from statistics, called distance correlation (and its partial variant), designed to evaluate correlation between feature spaces of different dimensions. We describe the steps necessary to carry out its deployment for large scale models -- this opens the door to a surprising array of applications ranging from conditioning one deep model w.r.t. another, learning disentangled representations as well as optimizing diverse models that would directly be more robust to adversarial attacks. Our experiments suggest a versatile regularizer (or constraint) with many advantages, which avoids some of the common difficulties one faces in such analyses. Code is at https://github.com/zhenxingjian/Partial_Distance_Correlation.

A First Look: Towards Explainable TextVQA Models via Visual and Textual Explanations

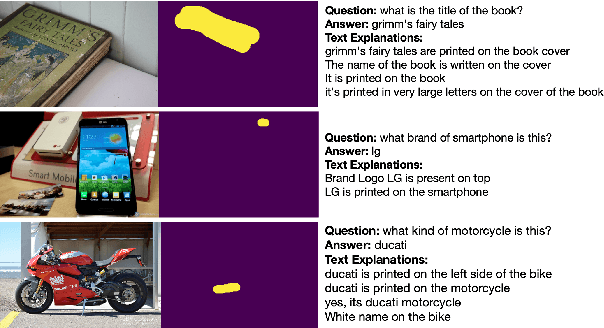
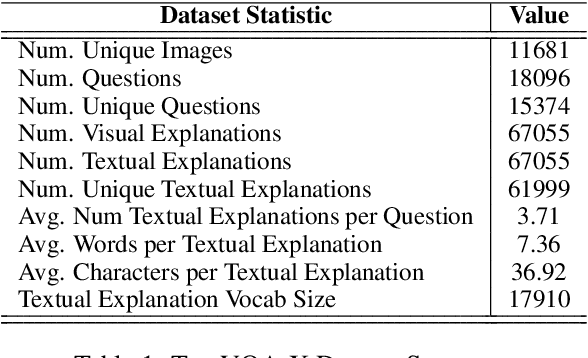
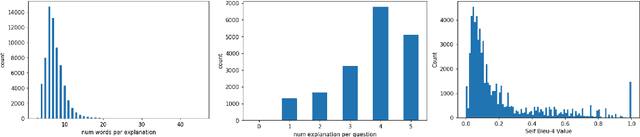
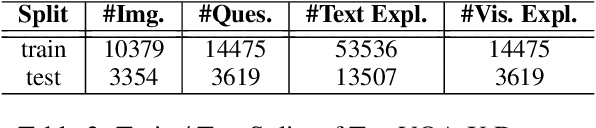
Explainable deep learning models are advantageous in many situations. Prior work mostly provide unimodal explanations through post-hoc approaches not part of the original system design. Explanation mechanisms also ignore useful textual information present in images. In this paper, we propose MTXNet, an end-to-end trainable multimodal architecture to generate multimodal explanations, which focuses on the text in the image. We curate a novel dataset TextVQA-X, containing ground truth visual and multi-reference textual explanations that can be leveraged during both training and evaluation. We then quantitatively show that training with multimodal explanations complements model performance and surpasses unimodal baselines by up to 7% in CIDEr scores and 2% in IoU. More importantly, we demonstrate that the multimodal explanations are consistent with human interpretations, help justify the models' decision, and provide useful insights to help diagnose an incorrect prediction. Finally, we describe a real-world e-commerce application for using the generated multimodal explanations.

Simpler Certified Radius Maximization by Propagating Covariances

One strategy for adversarially training a robust model is to maximize its certified radius -- the neighborhood around a given training sample for which the model's prediction remains unchanged. The scheme typically involves analyzing a "smoothed" classifier where one estimates the prediction corresponding to Gaussian samples in the neighborhood of each sample in the mini-batch, accomplished in practice by Monte Carlo sampling. In this paper, we investigate the hypothesis that this sampling bottleneck can potentially be mitigated by identifying ways to directly propagate the covariance matrix of the smoothed distribution through the network. To this end, we find that other than certain adjustments to the network, propagating the covariances must also be accompanied by additional accounting that keeps track of how the distributional moments transform and interact at each stage in the network. We show how satisfying these criteria yields an algorithm for maximizing the certified radius on datasets including Cifar-10, ImageNet, and Places365 while offering runtime savings on networks with moderate depth, with a small compromise in overall accuracy. We describe the details of the key modifications that enable practical use. Via various experiments, we evaluate when our simplifications are sensible, and what the key benefits and limitations are.

Flow-based Generative Models for Learning Manifold to Manifold Mappings

Many measurements or observations in computer vision and machine learning manifest as non-Euclidean data. While recent proposals (like spherical CNN) have extended a number of deep neural network architectures to manifold-valued data, and this has often provided strong improvements in performance, the literature on generative models for manifold data is quite sparse. Partly due to this gap, there are also no modality transfer/translation models for manifold-valued data whereas numerous such methods based on generative models are available for natural images. This paper addresses this gap, motivated by a need in brain imaging -- in doing so, we expand the operating range of certain generative models (as well as generative models for modality transfer) from natural images to images with manifold-valued measurements. Our main result is the design of a two-stream version of GLOW (flow-based invertible generative models) that can synthesize information of a field of one type of manifold-valued measurements given another. On the theoretical side, we introduce three kinds of invertible layers for manifold-valued data, which are not only analogous to their functionality in flow-based generative models (e.g., GLOW) but also preserve the key benefits (determinants of the Jacobian are easy to calculate). For experiments, on a large dataset from the Human Connectome Project (HCP), we show promising results where we can reliably and accurately reconstruct brain images of a field of orientation distribution functions (ODF) from diffusion tensor images (DTI), where the latter has a $5\times$ faster acquisition time but at the expense of worse angular resolution.

CPR-GCN: Conditional Partial-Residual Graph Convolutional Network in Automated Anatomical Labeling of Coronary Arteries

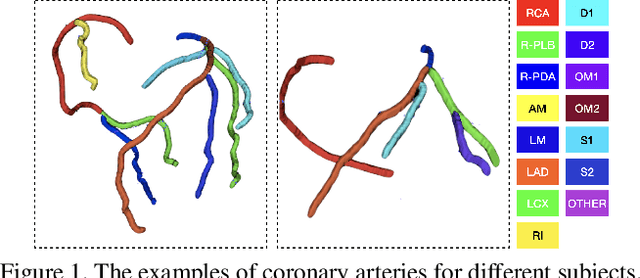
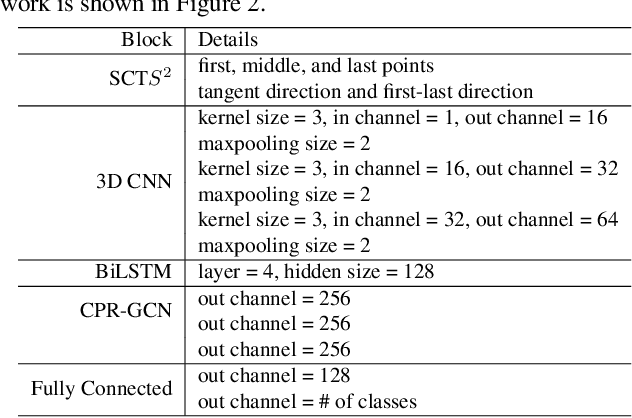
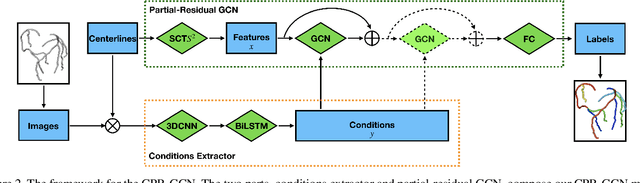
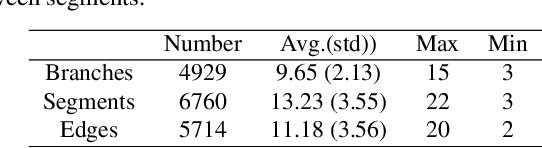
Automated anatomical labeling plays a vital role in coronary artery disease diagnosing procedure. The main challenge in this problem is the large individual variability inherited in human anatomy. Existing methods usually rely on the position information and the prior knowledge of the topology of the coronary artery tree, which may lead to unsatisfactory performance when the main branches are confusing. Motivated by the wide application of the graph neural network in structured data, in this paper, we propose a conditional partial-residual graph convolutional network (CPR-GCN), which takes both position and CT image into consideration, since CT image contains abundant information such as branch size and spanning direction. Two majority parts, a Partial-Residual GCN and a conditions extractor, are included in CPR-GCN. The conditions extractor is a hybrid model containing the 3D CNN and the LSTM, which can extract 3D spatial image features along the branches. On the technical side, the Partial-Residual GCN takes the position features of the branches, with the 3D spatial image features as conditions, to predict the label for each branches. While on the mathematical side, our approach twists the partial differential equation (PDE) into the graph modeling. A dataset with 511 subjects is collected from the clinic and annotated by two experts with a two-phase annotation process. According to the five-fold cross-validation, our CPR-GCN yields 95.8% meanRecall, 95.4% meanPrecision and 0.955 meanF1, which outperforms state-of-the-art approaches.

Dilated Convolutional Neural Networks for Sequential Manifold-valued Data

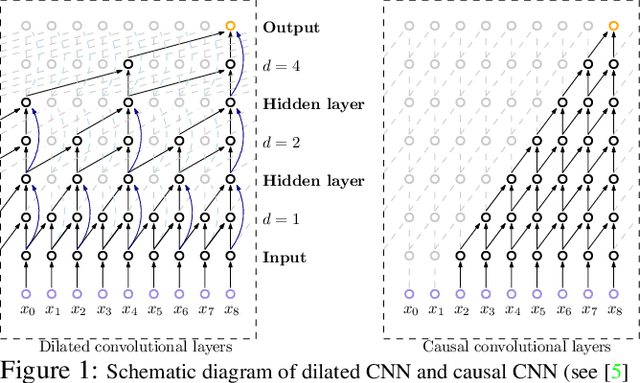
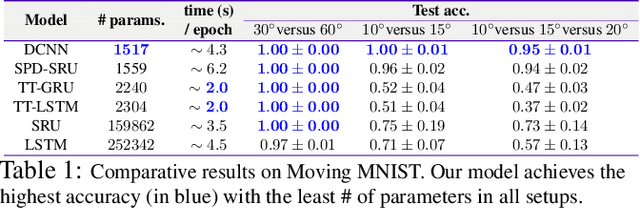
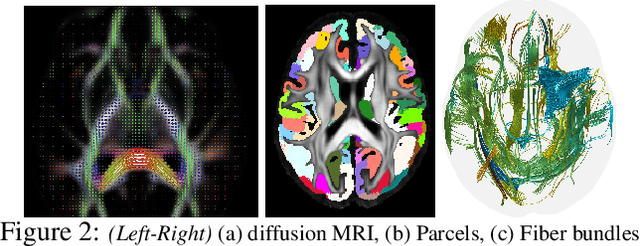
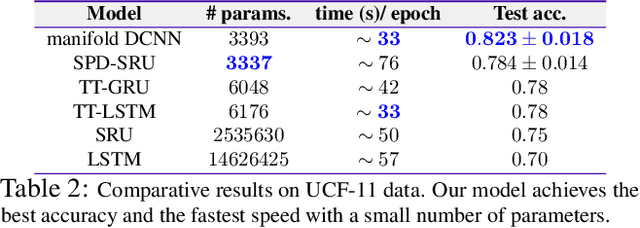
Efforts are underway to study ways via which the power of deep neural networks can be extended to non-standard data types such as structured data (e.g., graphs) or manifold-valued data (e.g., unit vectors or special matrices). Often, sizable empirical improvements are possible when the geometry of such data spaces are incorporated into the design of the model, architecture, and the algorithms. Motivated by neuroimaging applications, we study formulations where the data are {\em sequential manifold-valued measurements}. This case is common in brain imaging, where the samples correspond to symmetric positive definite matrices or orientation distribution functions. Instead of a recurrent model which poses computational/technical issues, and inspired by recent results showing the viability of dilated convolutional models for sequence prediction, we develop a dilated convolutional neural network architecture for this task. On the technical side, we show how the modules needed in our network can be derived while explicitly taking the Riemannian manifold structure into account. We show how the operations needed can leverage known results for calculating the weighted Fr\'{e}chet Mean (wFM). Finally, we present scientific results for group difference analysis in Alzheimer's disease (AD) where the groups are derived using AD pathology load: here the model finds several brain fiber bundles that are related to AD even when the subjects are all still cognitively healthy.

A Statistical Recurrent Model on the Manifold of Symmetric Positive Definite Matrices

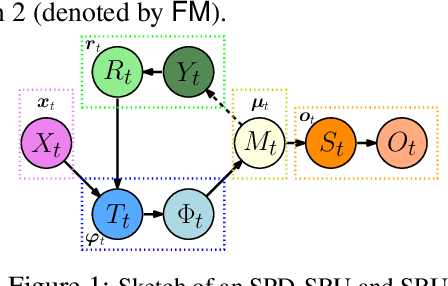
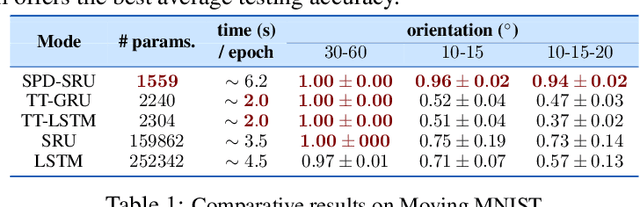
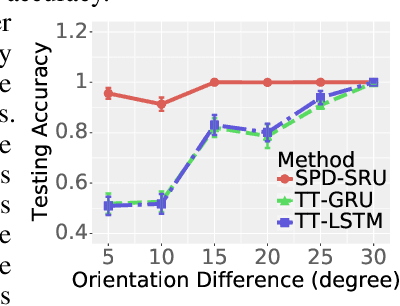
In a number of disciplines, the data (e.g., graphs, manifolds) to be analyzed are non-Euclidean in nature. Geometric deep learning corresponds to techniques that generalize deep neural network models to such non-Euclidean spaces. Several recent papers have shown how convolutional neural networks (CNNs) can be extended to learn with graph-based data. In this work, we study the setting where the data (or measurements) are ordered, longitudinal or temporal in nature and live on a Riemannian manifold -- this setting is common in a variety of problems in statistical machine learning, vision and medical imaging. We show how recurrent statistical recurrent network models can be defined in such spaces. We give an efficient algorithm and conduct a rigorous analysis of its statistical properties. We perform extensive numerical experiments demonstrating competitive performance with state of the art methods but with significantly less number of parameters. We also show applications to a statistical analysis task in brain imaging, a regime where deep neural network models have only been utilized in limited ways.