Dilated Convolutional Neural Networks for Sequential Manifold-valued Data
Paper and Code
Oct 05, 2019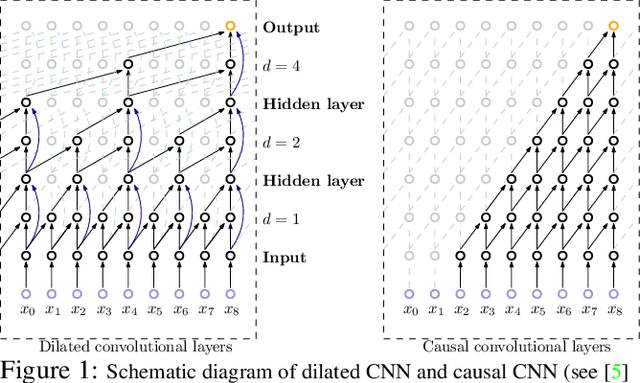
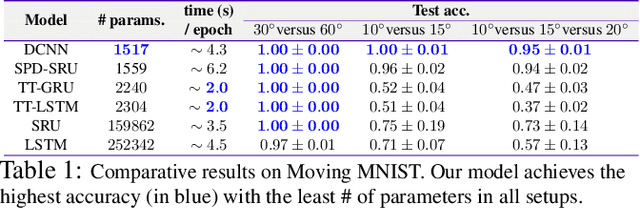
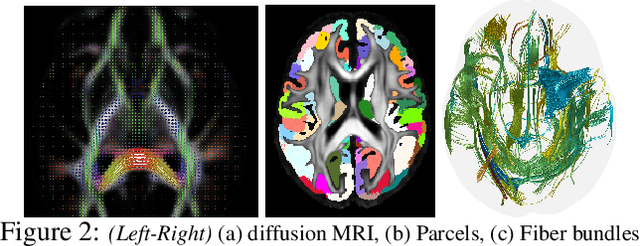
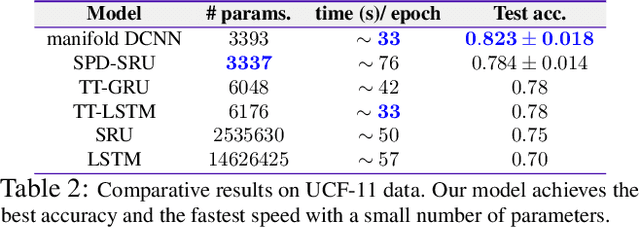
Efforts are underway to study ways via which the power of deep neural networks can be extended to non-standard data types such as structured data (e.g., graphs) or manifold-valued data (e.g., unit vectors or special matrices). Often, sizable empirical improvements are possible when the geometry of such data spaces are incorporated into the design of the model, architecture, and the algorithms. Motivated by neuroimaging applications, we study formulations where the data are {\em sequential manifold-valued measurements}. This case is common in brain imaging, where the samples correspond to symmetric positive definite matrices or orientation distribution functions. Instead of a recurrent model which poses computational/technical issues, and inspired by recent results showing the viability of dilated convolutional models for sequence prediction, we develop a dilated convolutional neural network architecture for this task. On the technical side, we show how the modules needed in our network can be derived while explicitly taking the Riemannian manifold structure into account. We show how the operations needed can leverage known results for calculating the weighted Fr\'{e}chet Mean (wFM). Finally, we present scientific results for group difference analysis in Alzheimer's disease (AD) where the groups are derived using AD pathology load: here the model finds several brain fiber bundles that are related to AD even when the subjects are all still cognitively healthy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge