Dilated Convolutional Neural Networks for Sequential Manifold-valued Data

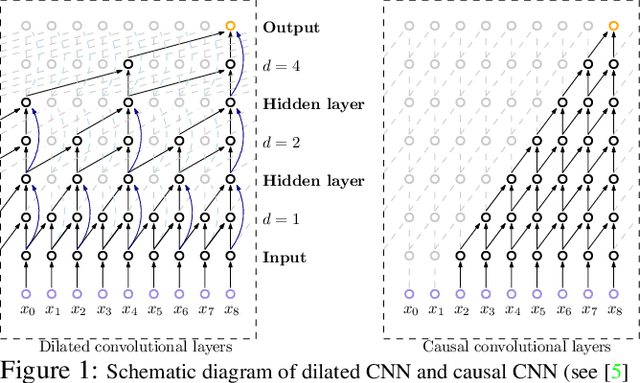
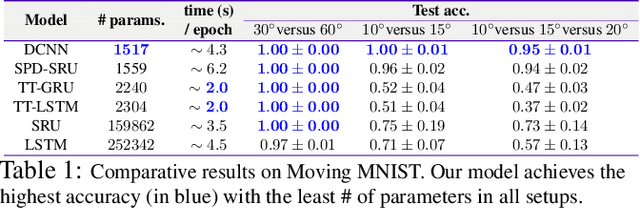
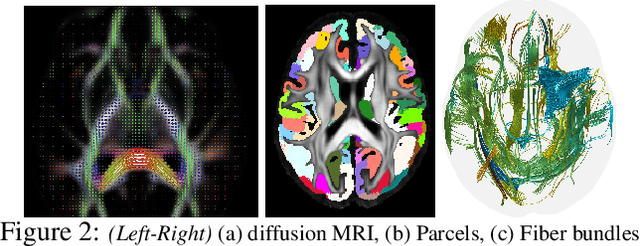
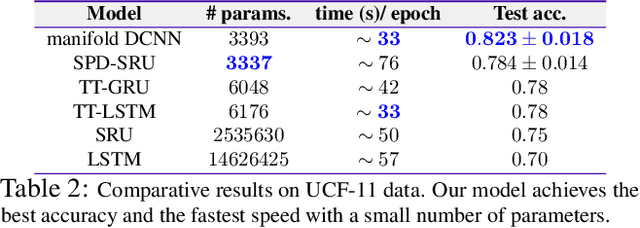
Efforts are underway to study ways via which the power of deep neural networks can be extended to non-standard data types such as structured data (e.g., graphs) or manifold-valued data (e.g., unit vectors or special matrices). Often, sizable empirical improvements are possible when the geometry of such data spaces are incorporated into the design of the model, architecture, and the algorithms. Motivated by neuroimaging applications, we study formulations where the data are {\em sequential manifold-valued measurements}. This case is common in brain imaging, where the samples correspond to symmetric positive definite matrices or orientation distribution functions. Instead of a recurrent model which poses computational/technical issues, and inspired by recent results showing the viability of dilated convolutional models for sequence prediction, we develop a dilated convolutional neural network architecture for this task. On the technical side, we show how the modules needed in our network can be derived while explicitly taking the Riemannian manifold structure into account. We show how the operations needed can leverage known results for calculating the weighted Fr\'{e}chet Mean (wFM). Finally, we present scientific results for group difference analysis in Alzheimer's disease (AD) where the groups are derived using AD pathology load: here the model finds several brain fiber bundles that are related to AD even when the subjects are all still cognitively healthy.

Diffeomorphic Metric Mapping and Probabilistic Atlas Generation of Hybrid Diffusion Imaging based on BFOR Signal Basis

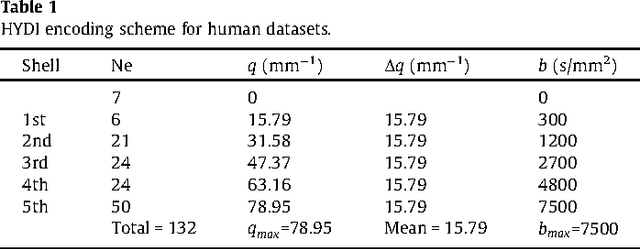
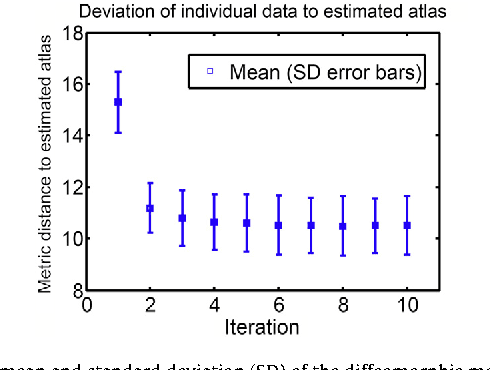
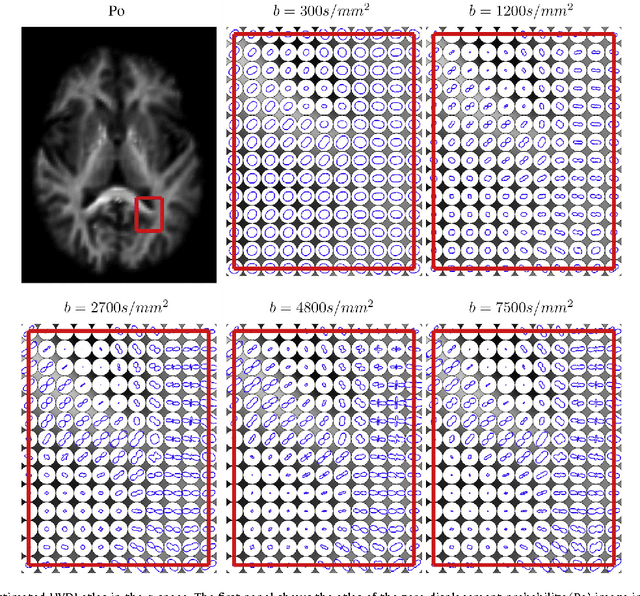
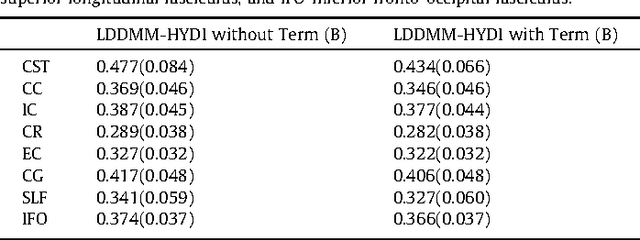
We propose a large deformation diffeomorphic metric mapping algorithm to align multiple b-value diffusion weighted imaging (mDWI) data, specifically acquired via hybrid diffusion imaging (HYDI), denoted as LDDMM-HYDI. We then propose a Bayesian model for estimating the white matter atlas from HYDIs. We adopt the work given in Hosseinbor et al. (2012) and represent the q-space diffusion signal with the Bessel Fourier orientation reconstruction (BFOR) signal basis. The BFOR framework provides the representation of mDWI in the q-space and thus reduces memory requirement. In addition, since the BFOR signal basis is orthonormal, the L2 norm that quantifies the differences in the q-space signals of any two mDWI datasets can be easily computed as the sum of the squared differences in the BFOR expansion coefficients. In this work, we show that the reorientation of the $q$-space signal due to spatial transformation can be easily defined on the BFOR signal basis. We incorporate the BFOR signal basis into the LDDMM framework and derive the gradient descent algorithm for LDDMM-HYDI with explicit orientation optimization. Additionally, we extend the previous Bayesian atlas estimation framework for scalar-valued images to HYDIs and derive the expectation-maximization algorithm for solving the HYDI atlas estimation problem. Using real HYDI datasets, we show the Bayesian model generates the white matter atlas with anatomical details. Moreover, we show that it is important to consider the variation of mDWI reorientation due to a small change in diffeomorphic transformation in the LDDMM-HYDI optimization and to incorporate the full information of HYDI for aligning mDWI.