Bayesian Estimation of White Matter Atlas from High Angular Resolution Diffusion Imaging

We present a Bayesian probabilistic model to estimate the brain white matter atlas from high angular resolution diffusion imaging (HARDI) data. This model incorporates a shape prior of the white matter anatomy and the likelihood of individual observed HARDI datasets. We first assume that the atlas is generated from a known hyperatlas through a flow of diffeomorphisms and its shape prior can be constructed based on the framework of large deformation diffeomorphic metric mapping (LDDMM). LDDMM characterizes a nonlinear diffeomorphic shape space in a linear space of initial momentum uniquely determining diffeomorphic geodesic flows from the hyperatlas. Therefore, the shape prior of the HARDI atlas can be modeled using a centered Gaussian random field (GRF) model of the initial momentum. In order to construct the likelihood of observed HARDI datasets, it is necessary to study the diffeomorphic transformation of individual observations relative to the atlas and the probabilistic distribution of orientation distribution functions (ODFs). To this end, we construct the likelihood related to the transformation using the same construction as discussed for the shape prior of the atlas. The probabilistic distribution of ODFs is then constructed based on the ODF Riemannian manifold. We assume that the observed ODFs are generated by an exponential map of random tangent vectors at the deformed atlas ODF. Hence, the likelihood of the ODFs can be modeled using a GRF of their tangent vectors in the ODF Riemannian manifold. We solve for the maximum a posteriori using the Expectation-Maximization algorithm and derive the corresponding update equations. Finally, we illustrate the HARDI atlas constructed based on a Chinese aging cohort of 94 adults and compare it with that generated by averaging the coefficients of spherical harmonics of the ODF across subjects.

Diffeomorphic Metric Mapping and Probabilistic Atlas Generation of Hybrid Diffusion Imaging based on BFOR Signal Basis

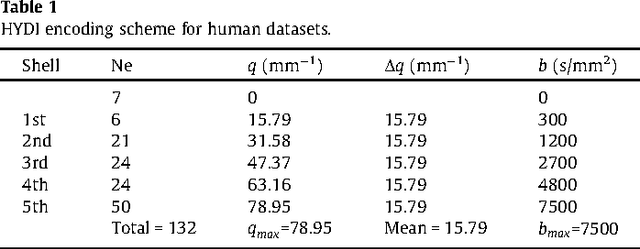
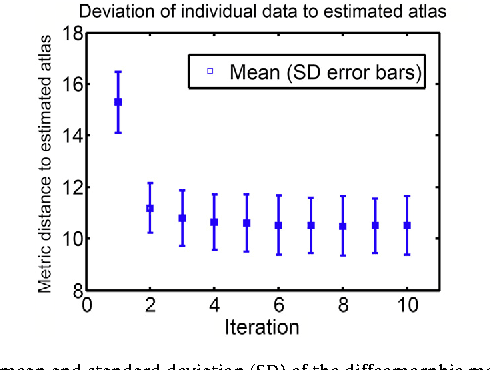
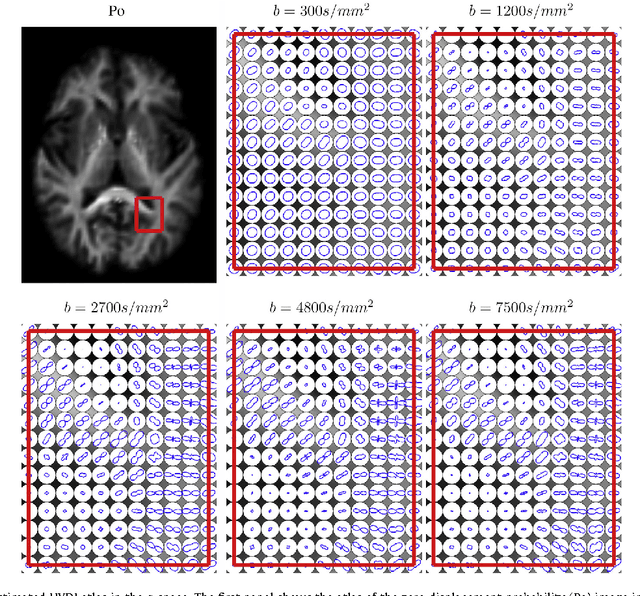
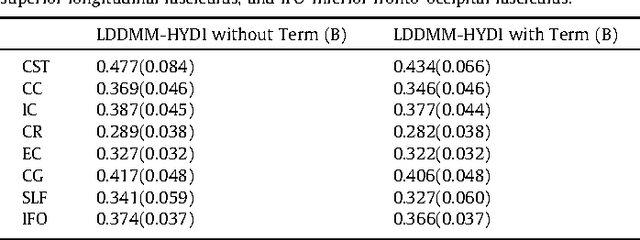
We propose a large deformation diffeomorphic metric mapping algorithm to align multiple b-value diffusion weighted imaging (mDWI) data, specifically acquired via hybrid diffusion imaging (HYDI), denoted as LDDMM-HYDI. We then propose a Bayesian model for estimating the white matter atlas from HYDIs. We adopt the work given in Hosseinbor et al. (2012) and represent the q-space diffusion signal with the Bessel Fourier orientation reconstruction (BFOR) signal basis. The BFOR framework provides the representation of mDWI in the q-space and thus reduces memory requirement. In addition, since the BFOR signal basis is orthonormal, the L2 norm that quantifies the differences in the q-space signals of any two mDWI datasets can be easily computed as the sum of the squared differences in the BFOR expansion coefficients. In this work, we show that the reorientation of the $q$-space signal due to spatial transformation can be easily defined on the BFOR signal basis. We incorporate the BFOR signal basis into the LDDMM framework and derive the gradient descent algorithm for LDDMM-HYDI with explicit orientation optimization. Additionally, we extend the previous Bayesian atlas estimation framework for scalar-valued images to HYDIs and derive the expectation-maximization algorithm for solving the HYDI atlas estimation problem. Using real HYDI datasets, we show the Bayesian model generates the white matter atlas with anatomical details. Moreover, we show that it is important to consider the variation of mDWI reorientation due to a small change in diffeomorphic transformation in the LDDMM-HYDI optimization and to incorporate the full information of HYDI for aligning mDWI.

Diffeomorphic Metric Mapping of High Angular Resolution Diffusion Imaging based on Riemannian Structure of Orientation Distribution Functions

In this paper, we propose a novel large deformation diffeomorphic registration algorithm to align high angular resolution diffusion images (HARDI) characterized by orientation distribution functions (ODFs). Our proposed algorithm seeks an optimal diffeomorphism of large deformation between two ODF fields in a spatial volume domain and at the same time, locally reorients an ODF in a manner such that it remains consistent with the surrounding anatomical structure. To this end, we first review the Riemannian manifold of ODFs. We then define the reorientation of an ODF when an affine transformation is applied and subsequently, define the diffeomorphic group action to be applied on the ODF based on this reorientation. We incorporate the Riemannian metric of ODFs for quantifying the similarity of two HARDI images into a variational problem defined under the large deformation diffeomorphic metric mapping (LDDMM) framework. We finally derive the gradient of the cost function in both Riemannian spaces of diffeomorphisms and the ODFs, and present its numerical implementation. Both synthetic and real brain HARDI data are used to illustrate the performance of our registration algorithm.