Topological Cycle Graph Attention Network for Brain Functional Connectivity

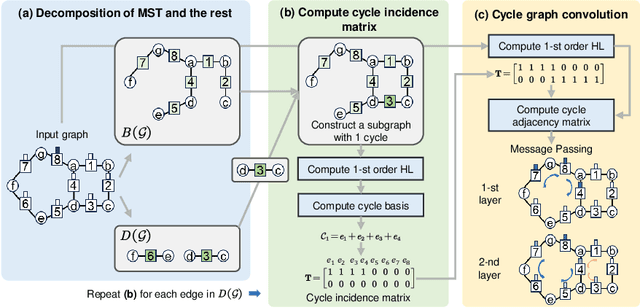
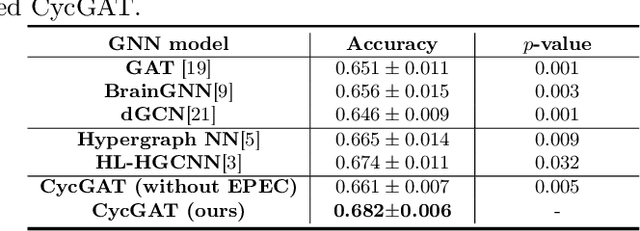
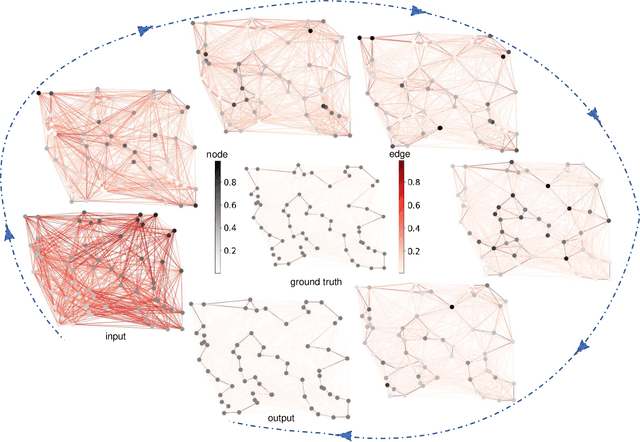
This study, we introduce a novel Topological Cycle Graph Attention Network (CycGAT), designed to delineate a functional backbone within brain functional graph--key pathways essential for signal transmissio--from non-essential, redundant connections that form cycles around this core structure. We first introduce a cycle incidence matrix that establishes an independent cycle basis within a graph, mapping its relationship with edges. We propose a cycle graph convolution that leverages a cycle adjacency matrix, derived from the cycle incidence matrix, to specifically filter edge signals in a domain of cycles. Additionally, we strengthen the representation power of the cycle graph convolution by adding an attention mechanism, which is further augmented by the introduction of edge positional encodings in cycles, to enhance the topological awareness of CycGAT. We demonstrate CycGAT's localization through simulation and its efficacy on an ABCD study's fMRI data (n=8765), comparing it with baseline models. CycGAT outperforms these models, identifying a functional backbone with significantly fewer cycles, crucial for understanding neural circuits related to general intelligence. Our code will be released once accepted.

Advancing Graph Neural Networks with HL-HGAT: A Hodge-Laplacian and Attention Mechanism Approach for Heterogeneous Graph-Structured Data

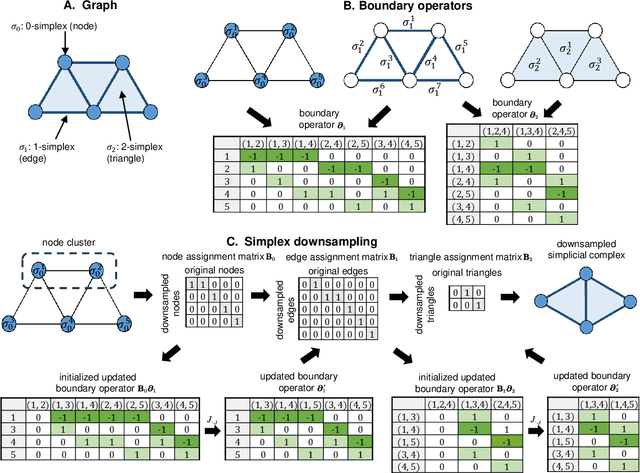
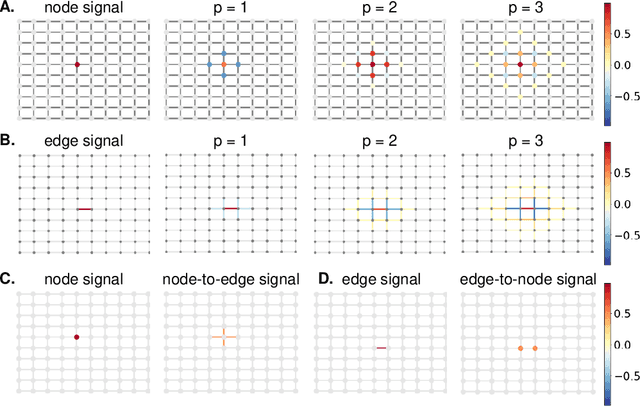
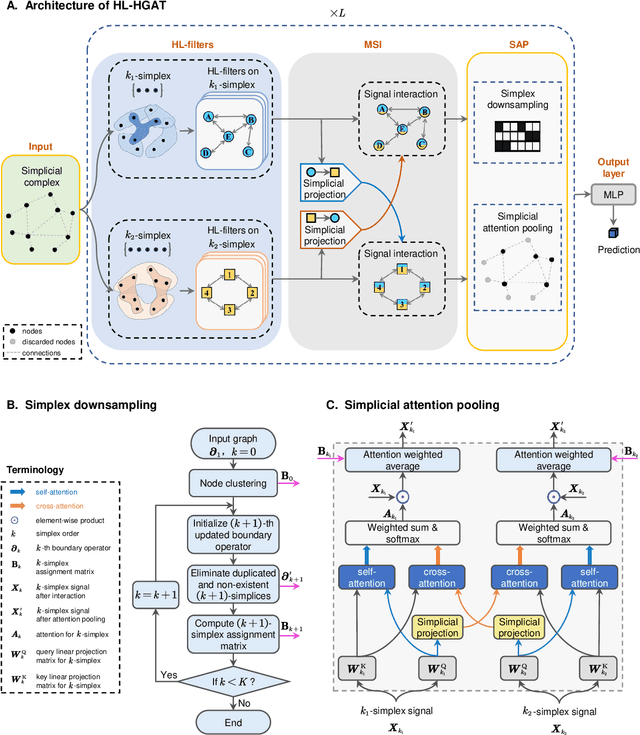
Graph neural networks (GNNs) have proven effective in capturing relationships among nodes in a graph. This study introduces a novel perspective by considering a graph as a simplicial complex, encompassing nodes, edges, triangles, and $k$-simplices, enabling the definition of graph-structured data on any $k$-simplices. Our contribution is the Hodge-Laplacian heterogeneous graph attention network (HL-HGAT), designed to learn heterogeneous signal representations across $k$-simplices. The HL-HGAT incorporates three key components: HL convolutional filters (HL-filters), simplicial projection (SP), and simplicial attention pooling (SAP) operators, applied to $k$-simplices. HL-filters leverage the unique topology of $k$-simplices encoded by the Hodge-Laplacian (HL) operator, operating within the spectral domain of the $k$-th HL operator. To address computation challenges, we introduce a polynomial approximation for HL-filters, exhibiting spatial localization properties. Additionally, we propose a pooling operator to coarsen $k$-simplices, combining features through simplicial attention mechanisms of self-attention and cross-attention via transformers and SP operators, capturing topological interconnections across multiple dimensions of simplices. The HL-HGAT is comprehensively evaluated across diverse graph applications, including NP-hard problems, graph multi-label and classification challenges, and graph regression tasks in logistics, computer vision, biology, chemistry, and neuroscience. The results demonstrate the model's efficacy and versatility in handling a wide range of graph-based scenarios.

Heterogeneous Graph Convolutional Neural Network via Hodge-Laplacian for Brain Functional Data

This study proposes a novel heterogeneous graph convolutional neural network (HGCNN) to handle complex brain fMRI data at regional and across-region levels. We introduce a generic formulation of spectral filters on heterogeneous graphs by introducing the $k-th$ Hodge-Laplacian (HL) operator. In particular, we propose Laguerre polynomial approximations of HL spectral filters and prove that their spatial localization on graphs is related to the polynomial order. Furthermore, based on the bijection property of boundary operators on simplex graphs, we introduce a generic topological graph pooling (TGPool) method that can be used at any dimensional simplices. This study designs HL-node, HL-edge, and HL-HGCNN neural networks to learn signal representation at a graph node, edge levels, and both, respectively. Our experiments employ fMRI from the Adolescent Brain Cognitive Development (ABCD; n=7693) to predict general intelligence. Our results demonstrate the advantage of the HL-edge network over the HL-node network when functional brain connectivity is considered as features. The HL-HGCNN outperforms the state-of-the-art graph neural networks (GNNs) approaches, such as GAT, BrainGNN, dGCN, BrainNetCNN, and Hypergraph NN. The functional connectivity features learned from the HL-HGCNN are meaningful in interpreting neural circuits related to general intelligence.

Revisiting convolutional neural network on graphs with polynomial approximations of Laplace-Beltrami spectral filtering

This paper revisits spectral graph convolutional neural networks (graph-CNNs) given in Defferrard (2016) and develops the Laplace-Beltrami CNN (LB-CNN) by replacing the graph Laplacian with the LB operator. We then define spectral filters via the LB operator on a graph. We explore the feasibility of Chebyshev, Laguerre, and Hermite polynomials to approximate LB-based spectral filters and define an update of the LB operator for pooling in the LBCNN. We employ the brain image data from Alzheimer's Disease Neuroimaging Initiative (ADNI) and demonstrate the use of the proposed LB-CNN. Based on the cortical thickness of the ADNI dataset, we showed that the LB-CNN didn't improve classification accuracy compared to the spectral graph-CNN. The three polynomials had a similar computational cost and showed comparable classification accuracy in the LB-CNN or spectral graph-CNN. Our findings suggest that even though the shapes of the three polynomials are different, deep learning architecture allows us to learn spectral filters such that the classification performance is not dependent on the type of the polynomials or the operators (graph Laplacian and LB operator).

Fast Mesh Data Augmentation via Chebyshev Polynomial of Spectral filtering

Deep neural networks have recently been recognized as one of the powerful learning techniques in computer vision and medical image analysis. Trained deep neural networks need to be generalizable to new data that was not seen before. In practice, there is often insufficient training data available and augmentation is used to expand the dataset. Even though graph convolutional neural network (graph-CNN) has been widely used in deep learning, there is a lack of augmentation methods to generate data on graphs or surfaces. This study proposes two unbiased augmentation methods, Laplace-Beltrami eigenfunction Data Augmentation (LB-eigDA) and Chebyshev polynomial Data Augmentation (C-pDA), to generate new data on surfaces, whose mean is the same as that of real data. LB-eigDA augments data via the resampling of the LB coefficients. In parallel with LB-eigDA, we introduce a fast augmentation approach, C-pDA, that employs a polynomial approximation of LB spectral filters on surfaces. We design LB spectral bandpass filters by Chebyshev polynomial approximation and resample signals filtered via these filters to generate new data on surfaces. We first validate LB-eigDA and C-pDA via simulated data and demonstrate their use for improving classification accuracy. We then employ the brain images of Alzheimer's Disease Neuroimaging Initiative (ADNI) and extract cortical thickness that is represented on the cortical surface to illustrate the use of the two augmentation methods. We demonstrate that augmented cortical thickness has a similar pattern to real data. Second, we show that C-pDA is much faster than LB-eigDA. Last, we show that C-pDA can improve the AD classification accuracy of graph-CNN.

Fast Polynomial Approximation of Heat Diffusion on Manifolds and Its Application to Brain Sulcal and Gyral Graph Pattern Analysis

Heat diffusion has been widely used in brain imaging for surface fairing, mesh regularization and noisy cortical data smoothing. In the previous spectral decomposition of graph Laplacian, Chebyshev polynomials were only used. In this paper, we present a new general spectral theory for the Laplace-Beltrami operator on a manifold that works for an arbitrary orthogonal polynomial with a recurrence relation. Besides the Chebyshev polynomials that was previous used in diffusion wavelets and convolutional neural networks, we provide three other polynomials to show the generality of the method. We also derive the closed-form solutions to the expansion coefficients of the spectral decomposition of the Laplace-Beltrami operator and use it to solve heat diffusion on a manifold for the first time. The proposed fast polynomial approximation scheme avoids solving for the eigenfunctions of the Laplace-Beltrami operator, which are computationally costly for large mesh size, and the numerical instability associated with the finite element method based diffusion solvers. The proposed method is applied in localizing the male and female differences in cortical sulcal and gyral graph patterns obtained from MRI.

Convolutional Neural Network on Semi-Regular Triangulated Meshes and its Application to Brain Image Data

We developed a convolution neural network (CNN) on semi-regular triangulated meshes whose vertices have 6 neighbours. The key blocks of the proposed CNN, including convolution and down-sampling, are directly defined in a vertex domain. By exploiting the ordering property of semi-regular meshes, the convolution is defined on a vertex domain with strong motivation from the spatial definition of classic convolution. Moreover, the down-sampling of a semi-regular mesh embedded in a 3D Euclidean space can achieve a down-sampling rate of 4, 16, 64, etc. We demonstrated the use of this vertex-based graph CNN for the classification of mild cognitive impairment (MCI) and Alzheimer's disease (AD) based on 3169 MRI scans of the Alzheimer's Disease Neuroimaging Initiative (ADNI). We compared the performance of the vertex-based graph CNN with that of the spectral graph CNN.

Unified Heat Kernel Regression for Diffusion, Kernel Smoothing and Wavelets on Manifolds and Its Application to Mandible Growth Modeling in CT Images

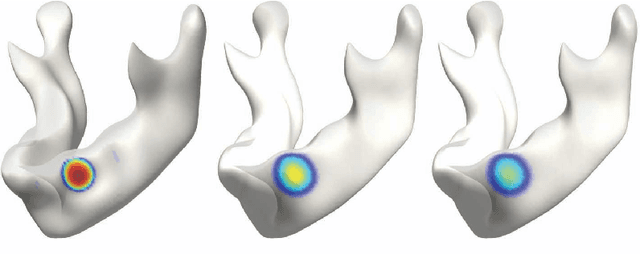
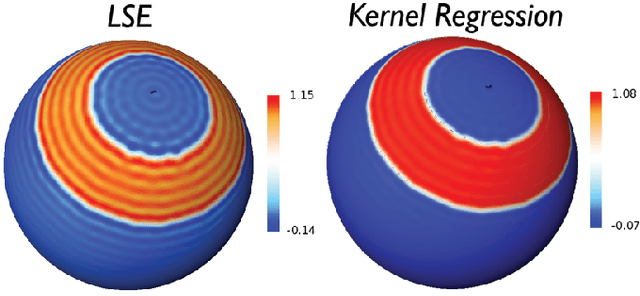
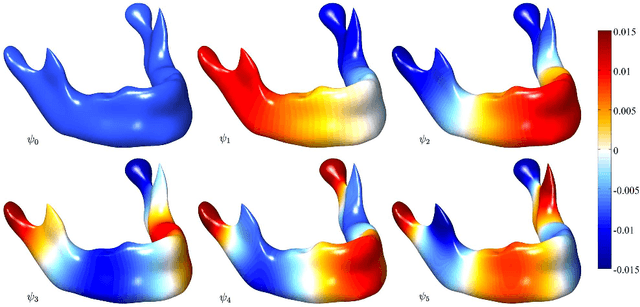
We present a novel kernel regression framework for smoothing scalar surface data using the Laplace-Beltrami eigenfunctions. Starting with the heat kernel constructed from the eigenfunctions, we formulate a new bivariate kernel regression framework as a weighted eigenfunction expansion with the heat kernel as the weights. The new kernel regression is mathematically equivalent to isotropic heat diffusion, kernel smoothing and recently popular diffusion wavelets. Unlike many previous partial differential equation based approaches involving diffusion, our approach represents the solution of diffusion analytically, reducing numerical inaccuracy and slow convergence. The numerical implementation is validated on a unit sphere using spherical harmonics. As an illustration, we have applied the method in characterizing the localized growth pattern of mandible surfaces obtained in CT images from subjects between ages 0 and 20 years by regressing the length of displacement vectors with respect to the template surface.

Bayesian Estimation of White Matter Atlas from High Angular Resolution Diffusion Imaging

We present a Bayesian probabilistic model to estimate the brain white matter atlas from high angular resolution diffusion imaging (HARDI) data. This model incorporates a shape prior of the white matter anatomy and the likelihood of individual observed HARDI datasets. We first assume that the atlas is generated from a known hyperatlas through a flow of diffeomorphisms and its shape prior can be constructed based on the framework of large deformation diffeomorphic metric mapping (LDDMM). LDDMM characterizes a nonlinear diffeomorphic shape space in a linear space of initial momentum uniquely determining diffeomorphic geodesic flows from the hyperatlas. Therefore, the shape prior of the HARDI atlas can be modeled using a centered Gaussian random field (GRF) model of the initial momentum. In order to construct the likelihood of observed HARDI datasets, it is necessary to study the diffeomorphic transformation of individual observations relative to the atlas and the probabilistic distribution of orientation distribution functions (ODFs). To this end, we construct the likelihood related to the transformation using the same construction as discussed for the shape prior of the atlas. The probabilistic distribution of ODFs is then constructed based on the ODF Riemannian manifold. We assume that the observed ODFs are generated by an exponential map of random tangent vectors at the deformed atlas ODF. Hence, the likelihood of the ODFs can be modeled using a GRF of their tangent vectors in the ODF Riemannian manifold. We solve for the maximum a posteriori using the Expectation-Maximization algorithm and derive the corresponding update equations. Finally, we illustrate the HARDI atlas constructed based on a Chinese aging cohort of 94 adults and compare it with that generated by averaging the coefficients of spherical harmonics of the ODF across subjects.

Diffeomorphic Metric Mapping and Probabilistic Atlas Generation of Hybrid Diffusion Imaging based on BFOR Signal Basis

We propose a large deformation diffeomorphic metric mapping algorithm to align multiple b-value diffusion weighted imaging (mDWI) data, specifically acquired via hybrid diffusion imaging (HYDI), denoted as LDDMM-HYDI. We then propose a Bayesian model for estimating the white matter atlas from HYDIs. We adopt the work given in Hosseinbor et al. (2012) and represent the q-space diffusion signal with the Bessel Fourier orientation reconstruction (BFOR) signal basis. The BFOR framework provides the representation of mDWI in the q-space and thus reduces memory requirement. In addition, since the BFOR signal basis is orthonormal, the L2 norm that quantifies the differences in the q-space signals of any two mDWI datasets can be easily computed as the sum of the squared differences in the BFOR expansion coefficients. In this work, we show that the reorientation of the $q$-space signal due to spatial transformation can be easily defined on the BFOR signal basis. We incorporate the BFOR signal basis into the LDDMM framework and derive the gradient descent algorithm for LDDMM-HYDI with explicit orientation optimization. Additionally, we extend the previous Bayesian atlas estimation framework for scalar-valued images to HYDIs and derive the expectation-maximization algorithm for solving the HYDI atlas estimation problem. Using real HYDI datasets, we show the Bayesian model generates the white matter atlas with anatomical details. Moreover, we show that it is important to consider the variation of mDWI reorientation due to a small change in diffeomorphic transformation in the LDDMM-HYDI optimization and to incorporate the full information of HYDI for aligning mDWI.