Dynamic Topological Data Analysis for Brain Networks via Wasserstein Graph Clustering

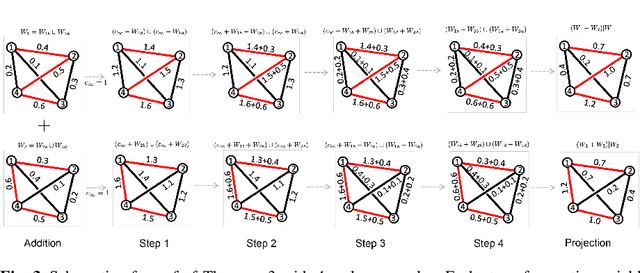
We present the novel Wasserstein graph clustering for dynamically changing graphs. The Wasserstein clustering penalizes the topological discrepancy between graphs. The Wasserstein clustering is shown to outperform the widely used k-means clustering. The method applied in more accurate determination of the state spaces of dynamically changing functional brain networks.

Revisiting convolutional neural network on graphs with polynomial approximations of Laplace-Beltrami spectral filtering

This paper revisits spectral graph convolutional neural networks (graph-CNNs) given in Defferrard (2016) and develops the Laplace-Beltrami CNN (LB-CNN) by replacing the graph Laplacian with the LB operator. We then define spectral filters via the LB operator on a graph. We explore the feasibility of Chebyshev, Laguerre, and Hermite polynomials to approximate LB-based spectral filters and define an update of the LB operator for pooling in the LBCNN. We employ the brain image data from Alzheimer's Disease Neuroimaging Initiative (ADNI) and demonstrate the use of the proposed LB-CNN. Based on the cortical thickness of the ADNI dataset, we showed that the LB-CNN didn't improve classification accuracy compared to the spectral graph-CNN. The three polynomials had a similar computational cost and showed comparable classification accuracy in the LB-CNN or spectral graph-CNN. Our findings suggest that even though the shapes of the three polynomials are different, deep learning architecture allows us to learn spectral filters such that the classification performance is not dependent on the type of the polynomials or the operators (graph Laplacian and LB operator).

Fast Mesh Data Augmentation via Chebyshev Polynomial of Spectral filtering

Deep neural networks have recently been recognized as one of the powerful learning techniques in computer vision and medical image analysis. Trained deep neural networks need to be generalizable to new data that was not seen before. In practice, there is often insufficient training data available and augmentation is used to expand the dataset. Even though graph convolutional neural network (graph-CNN) has been widely used in deep learning, there is a lack of augmentation methods to generate data on graphs or surfaces. This study proposes two unbiased augmentation methods, Laplace-Beltrami eigenfunction Data Augmentation (LB-eigDA) and Chebyshev polynomial Data Augmentation (C-pDA), to generate new data on surfaces, whose mean is the same as that of real data. LB-eigDA augments data via the resampling of the LB coefficients. In parallel with LB-eigDA, we introduce a fast augmentation approach, C-pDA, that employs a polynomial approximation of LB spectral filters on surfaces. We design LB spectral bandpass filters by Chebyshev polynomial approximation and resample signals filtered via these filters to generate new data on surfaces. We first validate LB-eigDA and C-pDA via simulated data and demonstrate their use for improving classification accuracy. We then employ the brain images of Alzheimer's Disease Neuroimaging Initiative (ADNI) and extract cortical thickness that is represented on the cortical surface to illustrate the use of the two augmentation methods. We demonstrate that augmented cortical thickness has a similar pattern to real data. Second, we show that C-pDA is much faster than LB-eigDA. Last, we show that C-pDA can improve the AD classification accuracy of graph-CNN.

Fast Polynomial Approximation of Heat Diffusion on Manifolds and Its Application to Brain Sulcal and Gyral Graph Pattern Analysis

Heat diffusion has been widely used in brain imaging for surface fairing, mesh regularization and noisy cortical data smoothing. In the previous spectral decomposition of graph Laplacian, Chebyshev polynomials were only used. In this paper, we present a new general spectral theory for the Laplace-Beltrami operator on a manifold that works for an arbitrary orthogonal polynomial with a recurrence relation. Besides the Chebyshev polynomials that was previous used in diffusion wavelets and convolutional neural networks, we provide three other polynomials to show the generality of the method. We also derive the closed-form solutions to the expansion coefficients of the spectral decomposition of the Laplace-Beltrami operator and use it to solve heat diffusion on a manifold for the first time. The proposed fast polynomial approximation scheme avoids solving for the eigenfunctions of the Laplace-Beltrami operator, which are computationally costly for large mesh size, and the numerical instability associated with the finite element method based diffusion solvers. The proposed method is applied in localizing the male and female differences in cortical sulcal and gyral graph patterns obtained from MRI.

Discrete Gyrator Transforms: Computational Algorithms and Applications

As an extension of the 2D fractional Fourier transform (FRFT) and a special case of the 2D linear canonical transform (LCT), the gyrator transform was introduced to produce rotations in twisted space/spatial-frequency planes. It is a useful tool in optics, signal processing and image processing. In this paper, we develop discrete gyrator transforms (DGTs) based on the 2D LCT. Taking the advantage of the additivity property of the 2D LCT, we propose three kinds of DGTs, each of which is a cascade of low-complexity operators. These DGTs have different constraints, characteristics, and properties, and are realized by different computational algorithms. Besides, we propose a kind of DGT based on the eigenfunctions of the gyrator transform. This DGT is an orthonormal transform, and thus its comprehensive properties, especially the additivity property, make it more useful in many applications. We also develop an efficient computational algorithm to significantly reduce the complexity of this DGT. At the end, a brief review of some important applications of the DGTs is presented, including mode conversion, sampling and reconstruction, watermarking, and image encryption.

Two-dimensional nonseparable discrete linear canonical transform based on CM-CC-CM-CC decomposition

As a generalization of the two-dimensional Fourier transform (2D FT) and 2D fractional Fourier transform, the 2D nonseparable linear canonical transform (2D NsLCT) is useful in optics, signal and image processing. To reduce the digital implementation complexity of the 2D NsLCT, some previous works decomposed the 2D NsLCT into several low-complexity operations, including 2D FT, 2D chirp multiplication (2D CM) and 2D affine transformations. However, 2D affine transformations will introduce interpolation error. In this paper, we propose a new decomposition called CM-CC-CM-CC decomposition, which decomposes the 2D NsLCT into two 2D CMs and two 2D chirp convolutions (2D CCs). No 2D affine transforms are involved. Simulation results show that the proposed methods have higher accuracy, lower computational complexity and smaller error in the additivity property compared with the previous works. Plus, the proposed methods have perfect reversibility property that one can reconstruct the input signal/image losslessly from the output.