Ilwoo Lyu
Random Multi-Channel Image Synthesis for Multiplexed Immunofluorescence Imaging
Sep 18, 2021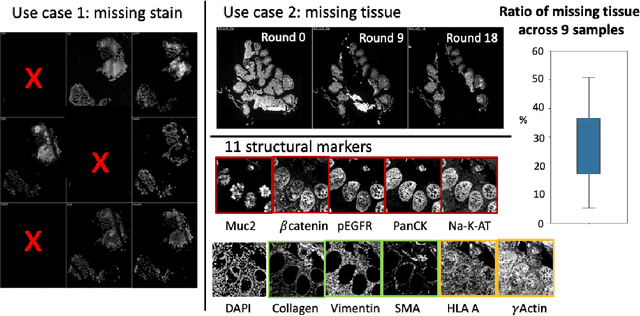
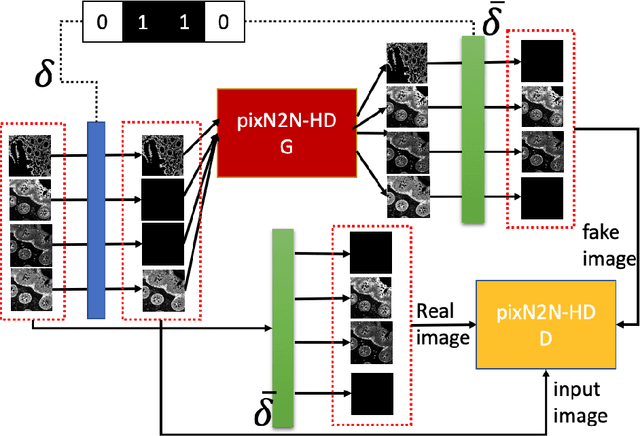
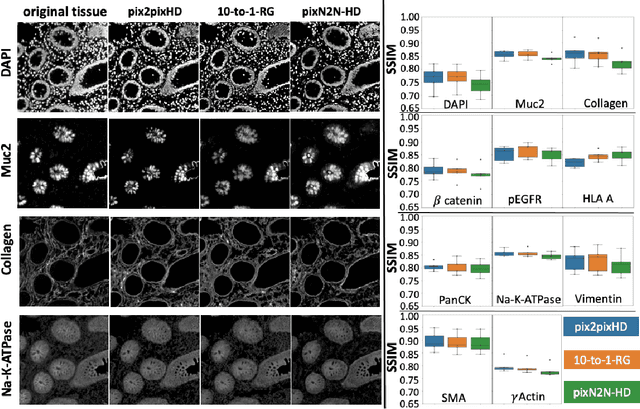
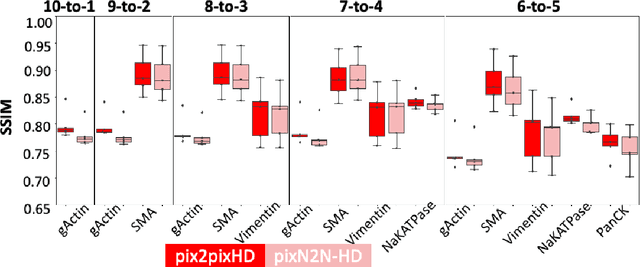
Abstract:Multiplex immunofluorescence (MxIF) is an emerging imaging technique that produces the high sensitivity and specificity of single-cell mapping. With a tenet of 'seeing is believing', MxIF enables iterative staining and imaging extensive antibodies, which provides comprehensive biomarkers to segment and group different cells on a single tissue section. However, considerable depletion of the scarce tissue is inevitable from extensive rounds of staining and bleaching ('missing tissue'). Moreover, the immunofluorescence (IF) imaging can globally fail for particular rounds ('missing stain''). In this work, we focus on the 'missing stain' issue. It would be appealing to develop digital image synthesis approaches to restore missing stain images without losing more tissue physically. Herein, we aim to develop image synthesis approaches for eleven MxIF structural molecular markers (i.e., epithelial and stromal) on real samples. We propose a novel multi-channel high-resolution image synthesis approach, called pixN2N-HD, to tackle possible missing stain scenarios via a high-resolution generative adversarial network (GAN). Our contribution is three-fold: (1) a single deep network framework is proposed to tackle missing stain in MxIF; (2) the proposed 'N-to-N' strategy reduces theoretical four years of computational time to 20 hours when covering all possible missing stains scenarios, with up to five missing stains (e.g., '(N-1)-to-1', '(N-2)-to-2'); and (3) this work is the first comprehensive experimental study of investigating cross-stain synthesis in MxIF. Our results elucidate a promising direction of advancing MxIF imaging with deep image synthesis.
Fast Polynomial Approximation of Heat Diffusion on Manifolds and Its Application to Brain Sulcal and Gyral Graph Pattern Analysis
Nov 07, 2019



Abstract:Heat diffusion has been widely used in brain imaging for surface fairing, mesh regularization and noisy cortical data smoothing. In the previous spectral decomposition of graph Laplacian, Chebyshev polynomials were only used. In this paper, we present a new general spectral theory for the Laplace-Beltrami operator on a manifold that works for an arbitrary orthogonal polynomial with a recurrence relation. Besides the Chebyshev polynomials that was previous used in diffusion wavelets and convolutional neural networks, we provide three other polynomials to show the generality of the method. We also derive the closed-form solutions to the expansion coefficients of the spectral decomposition of the Laplace-Beltrami operator and use it to solve heat diffusion on a manifold for the first time. The proposed fast polynomial approximation scheme avoids solving for the eigenfunctions of the Laplace-Beltrami operator, which are computationally costly for large mesh size, and the numerical instability associated with the finite element method based diffusion solvers. The proposed method is applied in localizing the male and female differences in cortical sulcal and gyral graph patterns obtained from MRI.
Enabling Multi-Shell b-Value Generalizability of Data-Driven Diffusion Models with Deep SHORE
Jul 15, 2019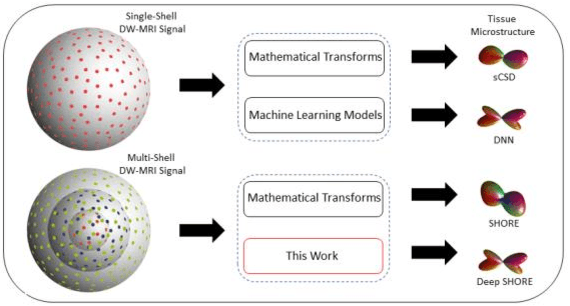
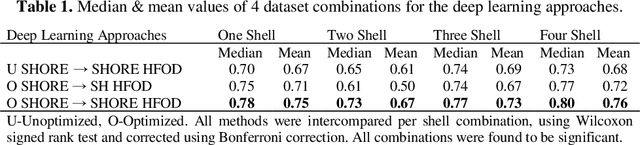
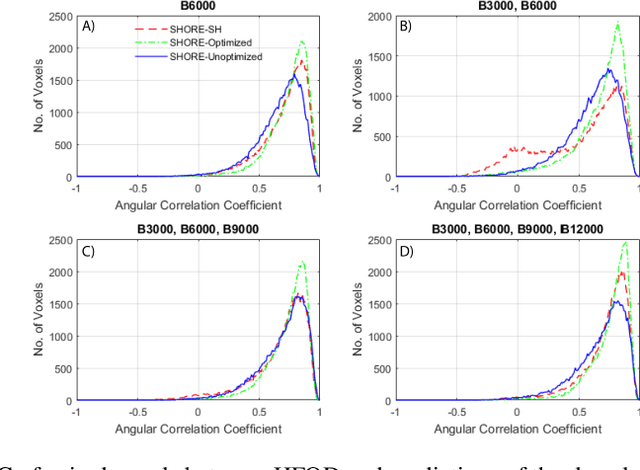
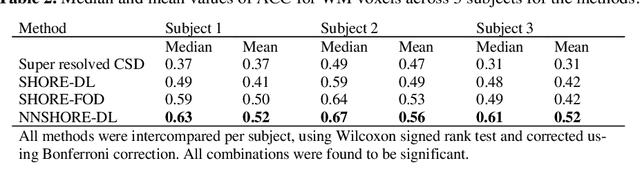
Abstract:Abstract. Intra-voxel models of the diffusion signal are essential for interpreting organization of the tissue environment at micrometer level with data at millimeter resolution. Recent advances in data driven methods have enabled direct compari-son and optimization of methods for in-vivo data with externally validated histological sections with both 2-D and 3-D histology. Yet, all existing methods make limiting assumptions of either (1) model-based linkages between b-values or (2) limited associations with single shell data. We generalize prior deep learning models that used single shell spherical harmonic transforms to integrate the re-cently developed simple harmonic oscillator reconstruction (SHORE) basis. To enable learning on the SHORE manifold, we present an alternative formulation of the fiber orientation distribution (FOD) object using the SHORE basis while rep-resenting the observed diffusion weighted data in the SHORE basis. To ensure consistency of hyper-parameter optimization for SHORE, we present our Deep SHORE approach to learn on a data-optimized manifold. Deep SHORE is evalu-ated with eight-fold cross-validation of a preclinical MRI-histology data with four b-values. Generalizability of in-vivo human data is evaluated on two separate 3T MRI scanners. Specificity in terms of angular correlation (ACC) with the preclinical data improved on single shell: 0.78 relative to 0.73 and 0.73, multi-shell: 0.80 relative to 0.74 (p < 0.001). In the in-vivo human data, Deep SHORE was more consistent across scanners with 0.63 relative to other multi-shell methods 0.39, 0.52 and 0.57 in terms of ACC. In conclusion, Deep SHORE is a promising method to enable data driven learning with DW-MRI under conditions with varying b-values, number of diffusion shells, and gradient directions per shell.
Inter-Scanner Harmonization of High Angular Resolution DW-MRI using Null Space Deep Learning
Oct 09, 2018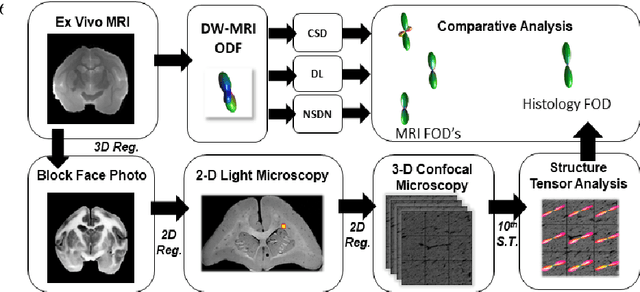
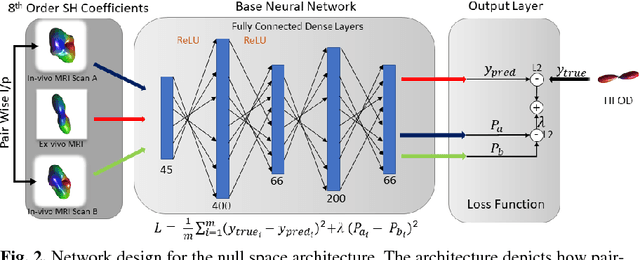

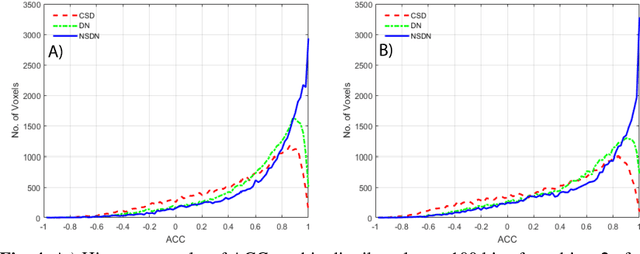
Abstract:Diffusion-weighted magnetic resonance imaging (DW-MRI) allows for non-invasive imaging of the local fiber architecture of the human brain at a millimetric scale. Multiple classical approaches have been proposed to detect both single (e.g., tensors) and multiple (e.g., constrained spherical deconvolution, CSD) fiber population orientations per voxel. However, existing techniques generally exhibit low reproducibility across MRI scanners. Herein, we propose a data-driven tech-nique using a neural network design which exploits two categories of data. First, training data were acquired on three squirrel monkey brains using ex-vivo DW-MRI and histology of the brain. Second, repeated scans of human subjects were acquired on two different scanners to augment the learning of the network pro-posed. To use these data, we propose a new network architecture, the null space deep network (NSDN), to simultaneously learn on traditional observed/truth pairs (e.g., MRI-histology voxels) along with repeated observations without a known truth (e.g., scan-rescan MRI). The NSDN was tested on twenty percent of the histology voxels that were kept completely blind to the network. NSDN significantly improved absolute performance relative to histology by 3.87% over CSD and 1.42% over a recently proposed deep neural network approach. More-over, it improved reproducibility on the paired data by 21.19% over CSD and 10.09% over a recently proposed deep approach. Finally, NSDN improved gen-eralizability of the model to a third in vivo human scanner (which was not used in training) by 16.08% over CSD and 10.41% over a recently proposed deep learn-ing approach. This work suggests that data-driven approaches for local fiber re-construction are more reproducible, informative and precise and offers a novel, practical method for determining these models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge