Advancing Graph Neural Networks with HL-HGAT: A Hodge-Laplacian and Attention Mechanism Approach for Heterogeneous Graph-Structured Data

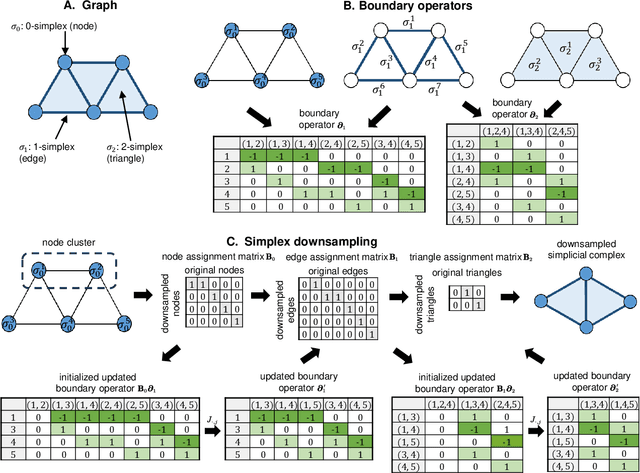
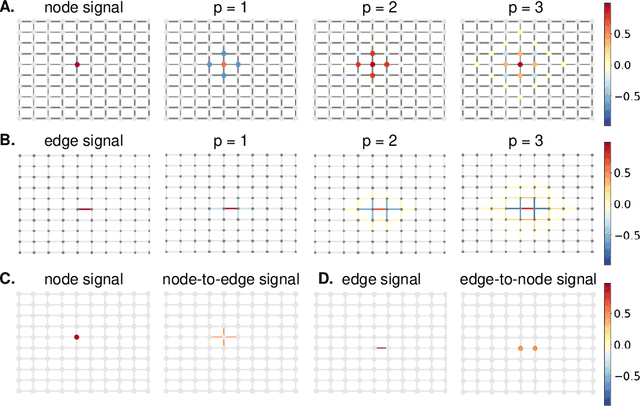
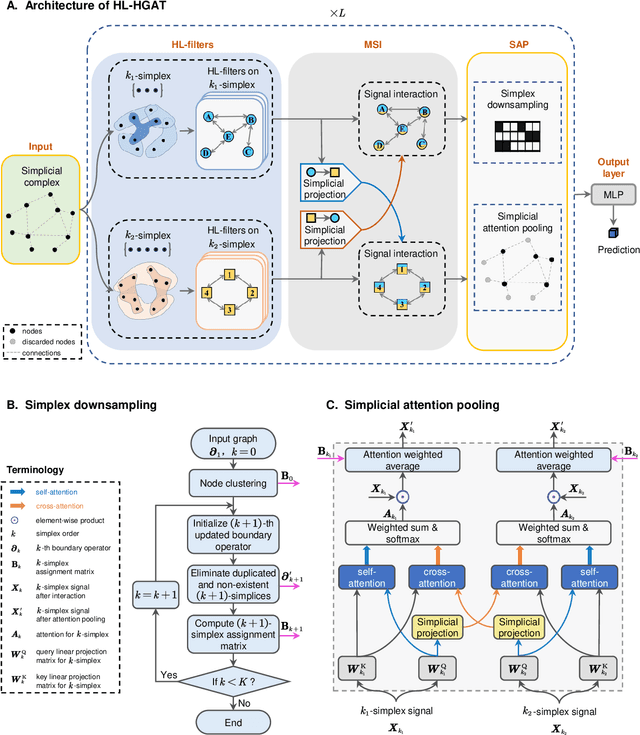
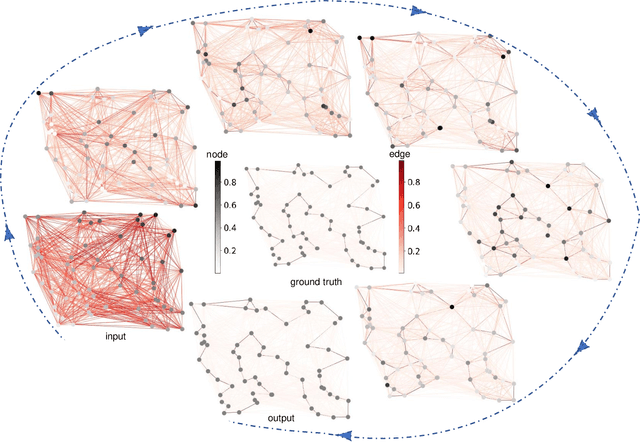
Graph neural networks (GNNs) have proven effective in capturing relationships among nodes in a graph. This study introduces a novel perspective by considering a graph as a simplicial complex, encompassing nodes, edges, triangles, and $k$-simplices, enabling the definition of graph-structured data on any $k$-simplices. Our contribution is the Hodge-Laplacian heterogeneous graph attention network (HL-HGAT), designed to learn heterogeneous signal representations across $k$-simplices. The HL-HGAT incorporates three key components: HL convolutional filters (HL-filters), simplicial projection (SP), and simplicial attention pooling (SAP) operators, applied to $k$-simplices. HL-filters leverage the unique topology of $k$-simplices encoded by the Hodge-Laplacian (HL) operator, operating within the spectral domain of the $k$-th HL operator. To address computation challenges, we introduce a polynomial approximation for HL-filters, exhibiting spatial localization properties. Additionally, we propose a pooling operator to coarsen $k$-simplices, combining features through simplicial attention mechanisms of self-attention and cross-attention via transformers and SP operators, capturing topological interconnections across multiple dimensions of simplices. The HL-HGAT is comprehensively evaluated across diverse graph applications, including NP-hard problems, graph multi-label and classification challenges, and graph regression tasks in logistics, computer vision, biology, chemistry, and neuroscience. The results demonstrate the model's efficacy and versatility in handling a wide range of graph-based scenarios.

Sulcal Pattern Matching with the Wasserstein Distance

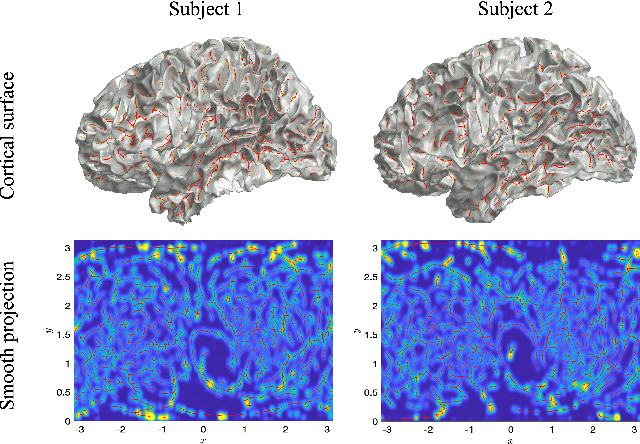
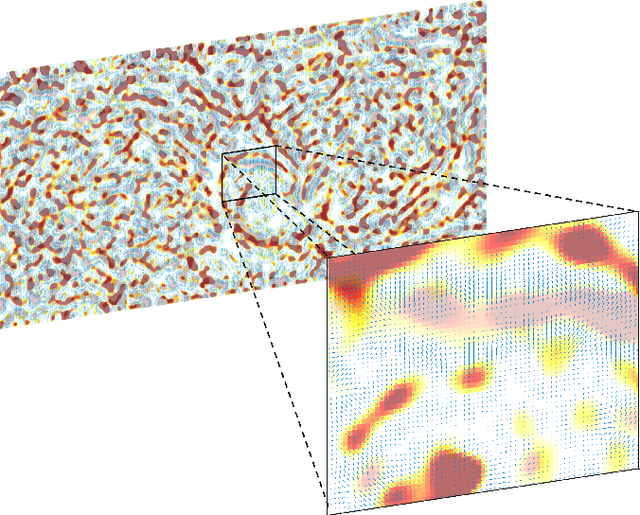
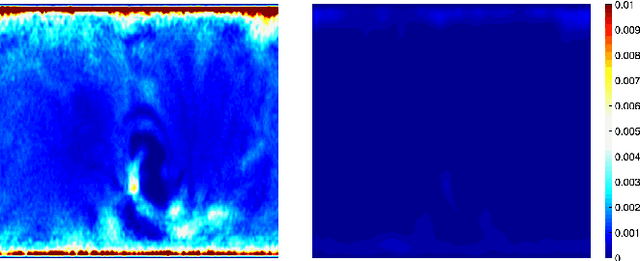
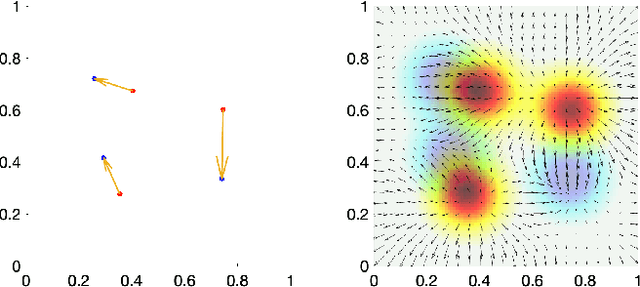
We present the unified computational framework for modeling the sulcal patterns of human brain obtained from the magnetic resonance images. The Wasserstein distance is used to align the sulcal patterns nonlinearly. These patterns are topologically different across subjects making the pattern matching a challenge. We work out the mathematical details and develop the gradient descent algorithms for estimating the deformation field. We further quantify the image registration performance. This method is applied in identifying the differences between male and female sulcal patterns.

Heterogeneous Graph Convolutional Neural Network via Hodge-Laplacian for Brain Functional Data

This study proposes a novel heterogeneous graph convolutional neural network (HGCNN) to handle complex brain fMRI data at regional and across-region levels. We introduce a generic formulation of spectral filters on heterogeneous graphs by introducing the $k-th$ Hodge-Laplacian (HL) operator. In particular, we propose Laguerre polynomial approximations of HL spectral filters and prove that their spatial localization on graphs is related to the polynomial order. Furthermore, based on the bijection property of boundary operators on simplex graphs, we introduce a generic topological graph pooling (TGPool) method that can be used at any dimensional simplices. This study designs HL-node, HL-edge, and HL-HGCNN neural networks to learn signal representation at a graph node, edge levels, and both, respectively. Our experiments employ fMRI from the Adolescent Brain Cognitive Development (ABCD; n=7693) to predict general intelligence. Our results demonstrate the advantage of the HL-edge network over the HL-node network when functional brain connectivity is considered as features. The HL-HGCNN outperforms the state-of-the-art graph neural networks (GNNs) approaches, such as GAT, BrainGNN, dGCN, BrainNetCNN, and Hypergraph NN. The functional connectivity features learned from the HL-HGCNN are meaningful in interpreting neural circuits related to general intelligence.

Dynamic Topological Data Analysis for Brain Networks via Wasserstein Graph Clustering

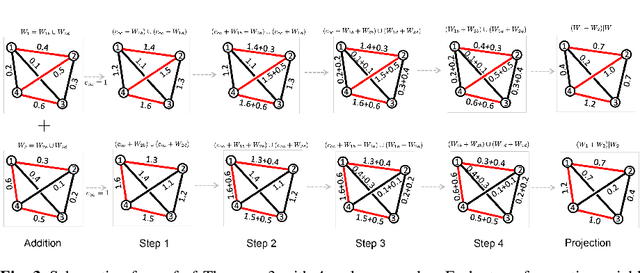
We present the novel Wasserstein graph clustering for dynamically changing graphs. The Wasserstein clustering penalizes the topological discrepancy between graphs. The Wasserstein clustering is shown to outperform the widely used k-means clustering. The method applied in more accurate determination of the state spaces of dynamically changing functional brain networks.

Topological Data Analysis of COVID-19 Virus Spike Proteins

Topological data analysis, including persistent homology, has undergone significant development in recent years. However, due to heterogenous nature of persistent homology features that do not have one-to-one correspondence across measurements, it is still difficult to build a coherent statistical inference procedure. The paired data structure in persistent homology as birth and death events of topological features add further complexity to conducting inference. To address these current problems, we propose to analyze the birth and death events using lattice paths. The proposed lattice path method is implemented to characterize the topological features of the protein structures of corona viruses. This demonstrates new insights to building a coherent statistical inference procedure in persistent homology.

Introduction to Brain and Medical Images

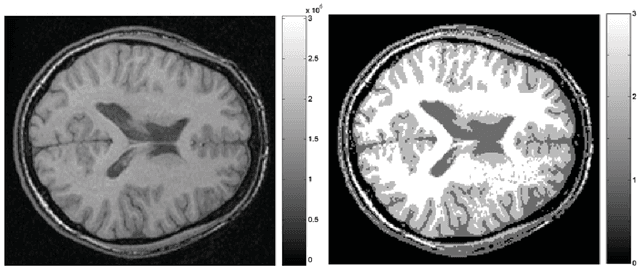
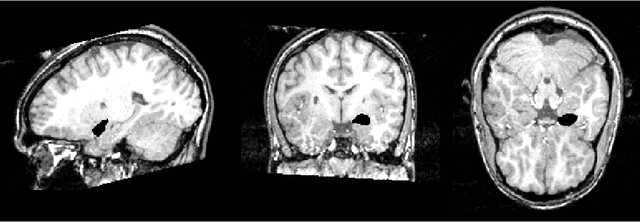
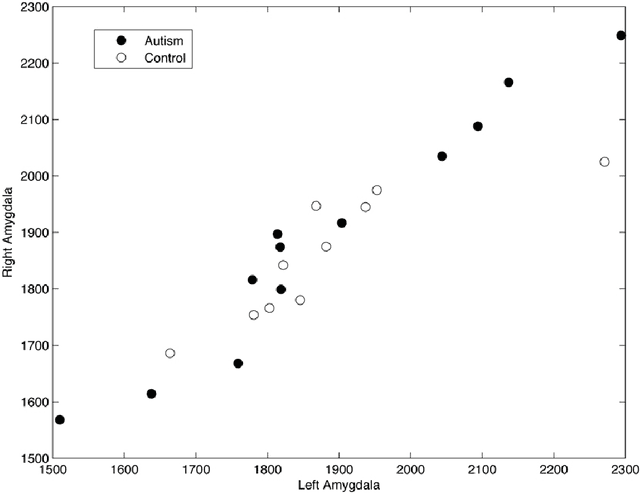
This article is based on the first chapter of book Chung (2013), where brain and medical images are introduced. The most widely used brain imaging modalities are magnetic resonance images (MRI), functional-MRI (fMRI) and diffusion tensor images (DTI). A brief introduction to each imaging modality is explained. Further, we explain what kind of curve, volume and surface data that can be extracted from each modality.

Revisiting convolutional neural network on graphs with polynomial approximations of Laplace-Beltrami spectral filtering

This paper revisits spectral graph convolutional neural networks (graph-CNNs) given in Defferrard (2016) and develops the Laplace-Beltrami CNN (LB-CNN) by replacing the graph Laplacian with the LB operator. We then define spectral filters via the LB operator on a graph. We explore the feasibility of Chebyshev, Laguerre, and Hermite polynomials to approximate LB-based spectral filters and define an update of the LB operator for pooling in the LBCNN. We employ the brain image data from Alzheimer's Disease Neuroimaging Initiative (ADNI) and demonstrate the use of the proposed LB-CNN. Based on the cortical thickness of the ADNI dataset, we showed that the LB-CNN didn't improve classification accuracy compared to the spectral graph-CNN. The three polynomials had a similar computational cost and showed comparable classification accuracy in the LB-CNN or spectral graph-CNN. Our findings suggest that even though the shapes of the three polynomials are different, deep learning architecture allows us to learn spectral filters such that the classification performance is not dependent on the type of the polynomials or the operators (graph Laplacian and LB operator).

Fast Mesh Data Augmentation via Chebyshev Polynomial of Spectral filtering

Deep neural networks have recently been recognized as one of the powerful learning techniques in computer vision and medical image analysis. Trained deep neural networks need to be generalizable to new data that was not seen before. In practice, there is often insufficient training data available and augmentation is used to expand the dataset. Even though graph convolutional neural network (graph-CNN) has been widely used in deep learning, there is a lack of augmentation methods to generate data on graphs or surfaces. This study proposes two unbiased augmentation methods, Laplace-Beltrami eigenfunction Data Augmentation (LB-eigDA) and Chebyshev polynomial Data Augmentation (C-pDA), to generate new data on surfaces, whose mean is the same as that of real data. LB-eigDA augments data via the resampling of the LB coefficients. In parallel with LB-eigDA, we introduce a fast augmentation approach, C-pDA, that employs a polynomial approximation of LB spectral filters on surfaces. We design LB spectral bandpass filters by Chebyshev polynomial approximation and resample signals filtered via these filters to generate new data on surfaces. We first validate LB-eigDA and C-pDA via simulated data and demonstrate their use for improving classification accuracy. We then employ the brain images of Alzheimer's Disease Neuroimaging Initiative (ADNI) and extract cortical thickness that is represented on the cortical surface to illustrate the use of the two augmentation methods. We demonstrate that augmented cortical thickness has a similar pattern to real data. Second, we show that C-pDA is much faster than LB-eigDA. Last, we show that C-pDA can improve the AD classification accuracy of graph-CNN.

Introduction to logistic regression

For random field theory based multiple comparison corrections In brain imaging, it is often necessary to compute the distribution of the supremum of a random field. Unfortunately, computing the distribution of the supremum of the random field is not easy and requires satisfying many distributional assumptions that may not be true in real data. Thus, there is a need to come up with a different framework that does not use the traditional statistical hypothesis testing paradigm that requires to compute p-values. With this as a motivation, we can use a different approach called the logistic regression that does not require computing the p-value and still be able to localize the regions of brain network differences. Unlike other discriminant and classification techniques that tried to classify preselected feature vectors, the method here does not require any preselected feature vectors and performs the classification at each edge level.

Gaussian kernel smoothing

Image acquisition and segmentation are likely to introduce noise. Further image processing such as image registration and parameterization can introduce additional noise. It is thus imperative to reduce noise measurements and boost signal. In order to increase the signal-to-noise ratio (SNR) and smoothness of data required for the subsequent random field theory based statistical inference, some type of smoothing is necessary. Among many image smoothing methods, Gaussian kernel smoothing has emerged as a de facto smoothing technique among brain imaging researchers due to its simplicity in numerical implementation. Gaussian kernel smoothing also increases statistical sensitivity and statistical power as well as Gausianness. Gaussian kernel smoothing can be viewed as weighted averaging of voxel values. Then from the central limit theorem, the weighted average should be more Gaussian.