Classification of High-dimensional Time Series in Spectral Domain using Explainable Features

Interpretable classification of time series presents significant challenges in high dimensions. Traditional feature selection methods in the frequency domain often assume sparsity in spectral density matrices (SDMs) or their inverses, which can be restrictive for real-world applications. In this article, we propose a model-based approach for classifying high-dimensional stationary time series by assuming sparsity in the difference between inverse SDMs. Our approach emphasizes the interpretability of model parameters, making it especially suitable for fields like neuroscience, where understanding differences in brain network connectivity across various states is crucial. The estimators for model parameters demonstrate consistency under appropriate conditions. We further propose using standard deep learning optimizers for parameter estimation, employing techniques such as mini-batching and learning rate scheduling. Additionally, we introduce a method to screen the most discriminatory frequencies for classification, which exhibits the sure screening property under general conditions. The flexibility of the proposed model allows the significance of covariates to vary across frequencies, enabling nuanced inferences and deeper insights into the underlying problem. The novelty of our method lies in the interpretability of the model parameters, addressing critical needs in neuroscience. The proposed approaches have been evaluated on simulated examples and the `Alert-vs-Drowsy' EEG dataset.

Predictive Performance Test based on the Exhaustive Nested Cross-Validation for High-dimensional data

It is crucial to assess the predictive performance of a model in order to establish its practicality and relevance in real-world scenarios, particularly for high-dimensional data analysis. Among data splitting or resampling methods, cross-validation (CV) is extensively used for several tasks such as estimating the prediction error, tuning the regularization parameter, and selecting the most suitable predictive model among competing alternatives. The K-fold cross-validation is a popular CV method but its limitation is that the risk estimates are highly dependent on the partitioning of the data (for training and testing). Here, the issues regarding the reproducibility of the K-fold CV estimator is demonstrated in hypothesis testing wherein different partitions lead to notably disparate conclusions. This study presents an alternative novel predictive performance test and valid confidence intervals based on exhaustive nested cross-validation for determining the difference in prediction error between two model-fitting algorithms. A naive implementation of the exhaustive nested cross-validation is computationally costly. Here, we address concerns regarding computational complexity by devising a computationally tractable closed-form expression for the proposed cross-validation estimator using ridge regularization. Our study also investigates strategies aimed at enhancing statistical power within high-dimensional scenarios while controlling the Type I error rate. To illustrate the practical utility of our method, we apply it to an RNA sequencing study and demonstrate its effectiveness in the context of biological data analysis.

Dynamic MRI reconstruction using low-rank plus sparse decomposition with smoothness regularization

The low-rank plus sparse (L+S) decomposition model has enabled better reconstruction of dynamic magnetic resonance imaging (dMRI) with separation into background (L) and dynamic (S) component. However, use of low-rank prior alone may not fully explain the slow variations or smoothness of the background part at the local scale. In this paper, we propose a smoothness-regularized L+S (SR-L+S) model for dMRI reconstruction from highly undersampled k-t-space data. We exploit joint low-rank and smooth priors on the background component of dMRI to better capture both its global and local temporal correlated structures. Extending the L+S formulation, the low-rank property is encoded by the nuclear norm, while the smoothness by a general \ell_{p}-norm penalty on the local differences of the columns of L. The additional smoothness regularizer can promote piecewise local consistency between neighboring frames. By smoothing out the noise and dynamic activities, it allows accurate recovery of the background part, and subsequently more robust dMRI reconstruction. Extensive experiments on multi-coil cardiac and synthetic data shows that the SR-L+S model outp

Stylized Projected GAN: A Novel Architecture for Fast and Realistic Image Generation

Generative Adversarial Networks are used for generating the data using a generator and a discriminator, GANs usually produce high-quality images, but training GANs in an adversarial setting is a difficult task. GANs require high computation power and hyper-parameter regularization for converging. Projected GANs tackle the training difficulty of GANs by using transfer learning to project the generated and real samples into a pre-trained feature space. Projected GANs improve the training time and convergence but produce artifacts in the generated images which reduce the quality of the generated samples, we propose an optimized architecture called Stylized Projected GANs which integrates the mapping network of the Style GANs with Skip Layer Excitation of Fast GAN. The integrated modules are incorporated within the generator architecture of the Fast GAN to mitigate the problem of artifacts in the generated images.

Graph-Regularized Manifold-Aware Conditional Wasserstein GAN for Brain Functional Connectivity Generation

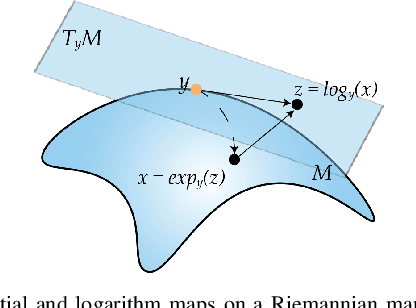
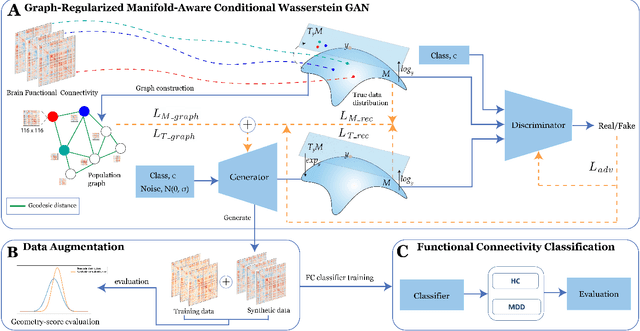
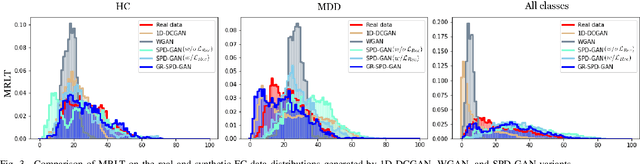
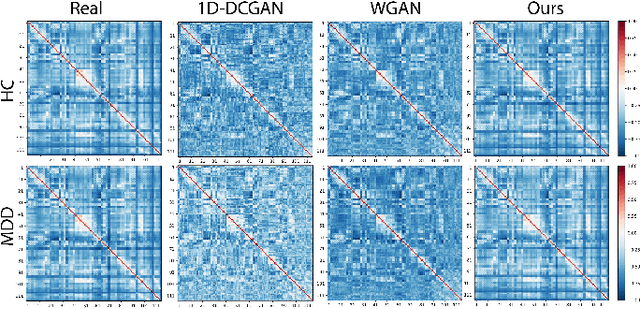
Common measures of brain functional connectivity (FC) including covariance and correlation matrices are semi-positive definite (SPD) matrices residing on a cone-shape Riemannian manifold. Despite its remarkable success for Euclidean-valued data generation, use of standard generative adversarial networks (GANs) to generate manifold-valued FC data neglects its inherent SPD structure and hence the inter-relatedness of edges in real FC. We propose a novel graph-regularized manifold-aware conditional Wasserstein GAN (GR-SPD-GAN) for FC data generation on the SPD manifold that can preserve the global FC structure. Specifically, we optimize a generalized Wasserstein distance between the real and generated SPD data under an adversarial training, conditioned on the class labels. The resulting generator can synthesize new SPD-valued FC matrices associated with different classes of brain networks, e.g., brain disorder or healthy control. Furthermore, we introduce additional population graph-based regularization terms on both the SPD manifold and its tangent space to encourage the generator to respect the inter-subject similarity of FC patterns in the real data. This also helps in avoiding mode collapse and produces more stable GAN training. Evaluated on resting-state functional magnetic resonance imaging (fMRI) data of major depressive disorder (MDD), qualitative and quantitative results show that the proposed GR-SPD-GAN clearly outperforms several state-of-the-art GANs in generating more realistic fMRI-based FC samples. When applied to FC data augmentation for MDD identification, classification models trained on augmented data generated by our approach achieved the largest margin of improvement in classification accuracy among the competing GANs over baselines without data augmentation.

Granger Causality using Neural Networks

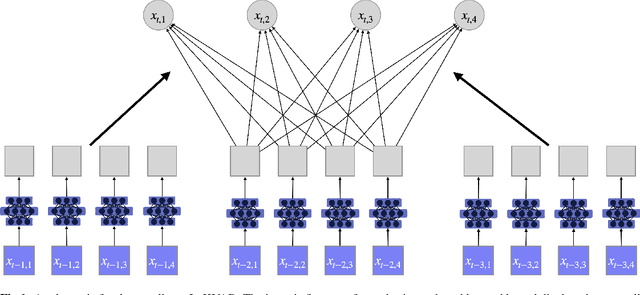
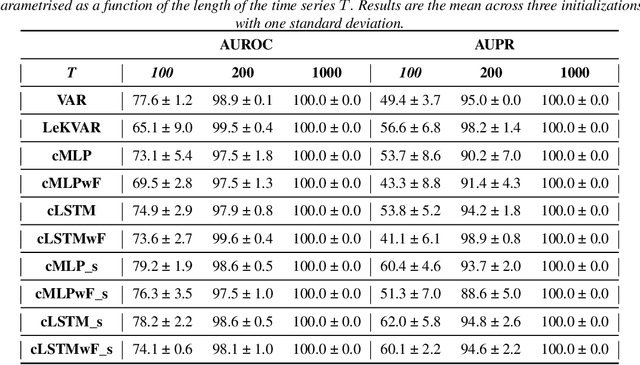
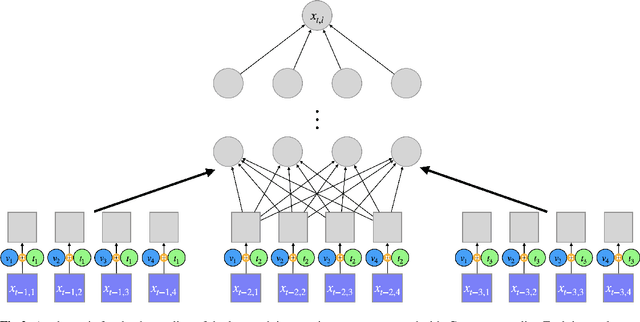
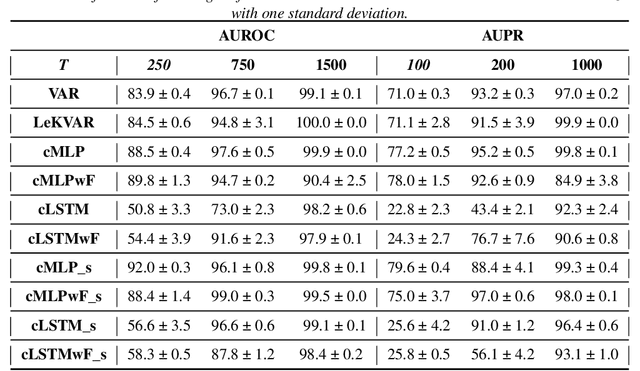
The Granger Causality (GC) test is a famous statistical hypothesis test for investigating if the past of one time series affects the future of the other. It helps in answering the question whether one time series is helpful in forecasting. Standard traditional approaches to Granger causality detection commonly assume linear dynamics, but such simplification does not hold in many real-world applications, e.g., neuroscience or genomics that are inherently non-linear. In such cases, imposing linear models such as Vector Autoregressive (VAR) models can lead to inconsistent estimation of true Granger Causal interactions. Machine Learning (ML) can learn the hidden patterns in the datasets specifically Deep Learning (DL) has shown tremendous promise in learning the non-linear dynamics of complex systems. Recent work of Tank et al propose to overcome the issue of linear simplification in VAR models by using neural networks combined with sparsity-inducing penalties on the learn-able weights. In this work, we build upon ideas introduced by Tank et al. We propose several new classes of models that can handle underlying non-linearity. Firstly, we present the Learned Kernal VAR(LeKVAR) model-an extension of VAR models that also learns kernel parametrized by a neural net. Secondly, we show one can directly decouple lags and individual time series importance via decoupled penalties. This decoupling provides better scaling and allows us to embed lag selection into RNNs. Lastly, we propose a new training algorithm that supports mini-batching, and it is compatible with commonly used adaptive optimizers such as Adam.he proposed techniques are evaluated on several simulated datasets inspired by real-world applications.We also apply these methods to the Electro-Encephalogram (EEG) data for an epilepsy patient to study the evolution of GC before , during and after seizure across the 19 EEG channels.

Graph Autoencoders for Embedding Learning in Brain Networks and Major Depressive Disorder Identification

Brain functional connectivity (FC) reveals biomarkers for identification of various neuropsychiatric disorders. Recent application of deep neural networks (DNNs) to connectome-based classification mostly relies on traditional convolutional neural networks using input connectivity matrices on a regular Euclidean grid. We propose a graph deep learning framework to incorporate the non-Euclidean information about graph structure for classifying functional magnetic resonance imaging (fMRI)- derived brain networks in major depressive disorder (MDD). We design a novel graph autoencoder (GAE) architecture based on the graph convolutional networks (GCNs) to embed the topological structure and node content of large-sized fMRI networks into low-dimensional latent representations. In network construction, we employ the Ledoit-Wolf (LDW) shrinkage method to estimate the high-dimensional FC metrics efficiently from fMRI data. We consider both supervised and unsupervised approaches for the graph embedded learning. The learned embeddings are then used as feature inputs for a deep fully-connected neural network (FCNN) to discriminate MDD from healthy controls. Evaluated on a resting-state fMRI MDD dataset with 43 subjects, results show that the proposed GAE-FCNN model significantly outperforms several state-of-the-art DNN methods for brain connectome classification, achieving accuracy of 72.50% using the LDW-FC metrics as node features. The graph embeddings of fMRI FC networks learned by the GAE also reveal apparent group differences between MDD and HC. Our new framework demonstrates feasibility of learning graph embeddings on brain networks to provide discriminative information for diagnosis of brain disorders.

Topological Data Analysis of COVID-19 Virus Spike Proteins

Topological data analysis, including persistent homology, has undergone significant development in recent years. However, due to heterogenous nature of persistent homology features that do not have one-to-one correspondence across measurements, it is still difficult to build a coherent statistical inference procedure. The paired data structure in persistent homology as birth and death events of topological features add further complexity to conducting inference. To address these current problems, we propose to analyze the birth and death events using lattice paths. The proposed lattice path method is implemented to characterize the topological features of the protein structures of corona viruses. This demonstrates new insights to building a coherent statistical inference procedure in persistent homology.

Separating Stimulus-Induced and Background Components of Dynamic Functional Connectivity in Naturalistic fMRI

We consider the challenges in extracting stimulus-related neural dynamics from other intrinsic processes and noise in naturalistic functional magnetic resonance imaging (fMRI). Most studies rely on inter-subject correlations (ISC) of low-level regional activity and neglect varying responses in individuals. We propose a novel, data-driven approach based on low-rank plus sparse (L+S) decomposition to isolate stimulus-driven dynamic changes in brain functional connectivity (FC) from the background noise, by exploiting shared network structure among subjects receiving the same naturalistic stimuli. The time-resolved multi-subject FC matrices are modeled as a sum of a low-rank component of correlated FC patterns across subjects, and a sparse component of subject-specific, idiosyncratic background activities. To recover the shared low-rank subspace, we introduce a fused version of principal component pursuit (PCP) by adding a fusion-type penalty on the differences between the rows of the low-rank matrix. The method improves the detection of stimulus-induced group-level homogeneity in the FC profile while capturing inter-subject variability. We develop an efficient algorithm via a linearized alternating direction method of multipliers to solve the fused-PCP. Simulations show accurate recovery by the fused-PCP even when a large fraction of FC edges are severely corrupted. When applied to natural fMRI data, our method reveals FC changes that were time-locked to auditory processing during movie watching, with dynamic engagement of sensorimotor systems for speech-in-noise. It also provides a better mapping to auditory content in the movie than ISC.

Detecting Dynamic Community Structure in Functional Brain Networks Across Individuals: A Multilayer Approach

We present a unified statistical framework for characterizing community structure of brain functional networks that captures variation across individuals and evolution over time. Existing methods for community detection focus only on single-subject analysis of dynamic networks; while recent extensions to multiple-subjects analysis are limited to static networks. To overcome these limitations, we propose a multi-subject, Markov-switching stochastic block model (MSS-SBM) to identify state-related changes in brain community organization over a group of individuals. We first formulate a multilayer extension of SBM to describe the time-dependent, multi-subject brain networks. We develop a novel procedure for fitting the multilayer SBM that builds on multislice modularity maximization which can uncover a common community partition of all layers (subjects) simultaneously. By augmenting with a dynamic Markov switching process, our proposed method is able to capture a set of distinct, recurring temporal states with respect to inter-community interactions over subjects and the change points between them. Simulation shows accurate community recovery and tracking of dynamic community regimes over multilayer networks by the MSS-SBM. Application to task fMRI reveals meaningful non-assortative brain community motifs, e.g., core-periphery structure at the group level, that are associated with language comprehension and motor functions suggesting their putative role in complex information integration. Our approach detected dynamic reconfiguration of modular connectivity elicited by varying task demands and identified unique profiles of intra and inter-community connectivity across different task conditions. The proposed multilayer network representation provides a principled way of detecting synchronous, dynamic modularity in brain networks across subjects.