Granger Causality using Neural Networks
Paper and Code
Aug 07, 2022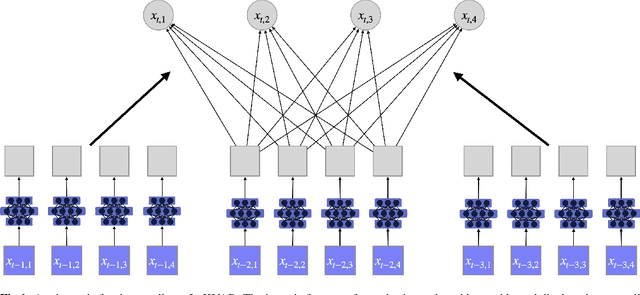
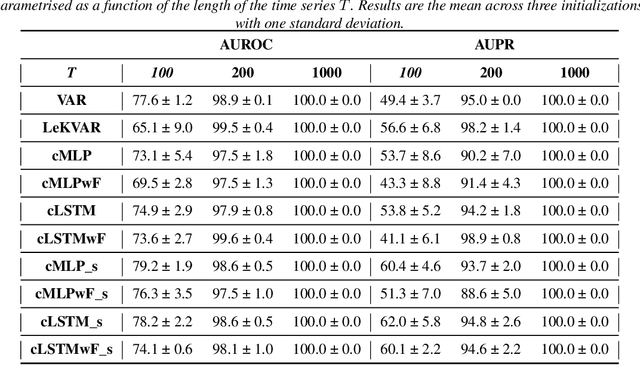
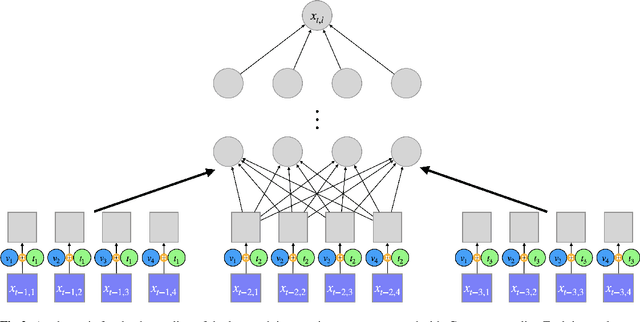
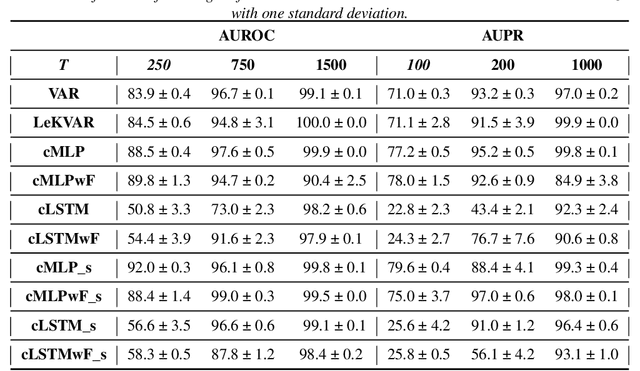
The Granger Causality (GC) test is a famous statistical hypothesis test for investigating if the past of one time series affects the future of the other. It helps in answering the question whether one time series is helpful in forecasting. Standard traditional approaches to Granger causality detection commonly assume linear dynamics, but such simplification does not hold in many real-world applications, e.g., neuroscience or genomics that are inherently non-linear. In such cases, imposing linear models such as Vector Autoregressive (VAR) models can lead to inconsistent estimation of true Granger Causal interactions. Machine Learning (ML) can learn the hidden patterns in the datasets specifically Deep Learning (DL) has shown tremendous promise in learning the non-linear dynamics of complex systems. Recent work of Tank et al propose to overcome the issue of linear simplification in VAR models by using neural networks combined with sparsity-inducing penalties on the learn-able weights. In this work, we build upon ideas introduced by Tank et al. We propose several new classes of models that can handle underlying non-linearity. Firstly, we present the Learned Kernal VAR(LeKVAR) model-an extension of VAR models that also learns kernel parametrized by a neural net. Secondly, we show one can directly decouple lags and individual time series importance via decoupled penalties. This decoupling provides better scaling and allows us to embed lag selection into RNNs. Lastly, we propose a new training algorithm that supports mini-batching, and it is compatible with commonly used adaptive optimizers such as Adam.he proposed techniques are evaluated on several simulated datasets inspired by real-world applications.We also apply these methods to the Electro-Encephalogram (EEG) data for an epilepsy patient to study the evolution of GC before , during and after seizure across the 19 EEG channels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge