SFC-GAN: A Generative Adversarial Network for Brain Functional and Structural Connectome Translation

Modern brain imaging technologies have enabled the detailed reconstruction of human brain connectomes, capturing structural connectivity (SC) from diffusion MRI and functional connectivity (FC) from functional MRI. Understanding the intricate relationships between SC and FC is vital for gaining deeper insights into the brain's functional and organizational mechanisms. However, obtaining both SC and FC modalities simultaneously remains challenging, hindering comprehensive analyses. Existing deep generative models typically focus on synthesizing a single modality or unidirectional translation between FC and SC, thereby missing the potential benefits of bi-directional translation, especially in scenarios where only one connectome is available. Therefore, we propose Structural-Functional Connectivity GAN (SFC-GAN), a novel framework for bidirectional translation between SC and FC. This approach leverages the CycleGAN architecture, incorporating convolutional layers to effectively capture the spatial structures of brain connectomes. To preserve the topological integrity of these connectomes, we employ a structure-preserving loss that guides the model in capturing both global and local connectome patterns while maintaining symmetry. Our framework demonstrates superior performance in translating between SC and FC, outperforming baseline models in similarity and graph property evaluations compared to ground truth data, each translated modality can be effectively utilized for downstream classification.

Graph-Regularized Manifold-Aware Conditional Wasserstein GAN for Brain Functional Connectivity Generation

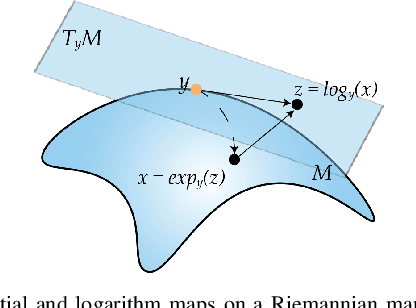
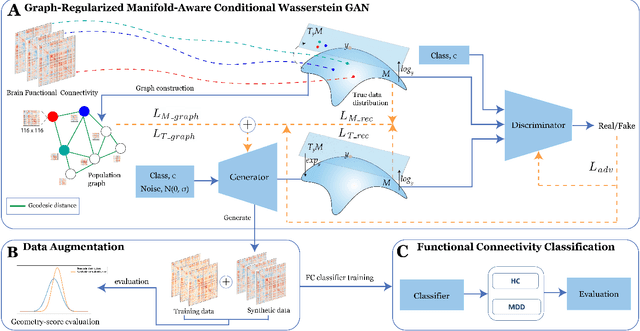
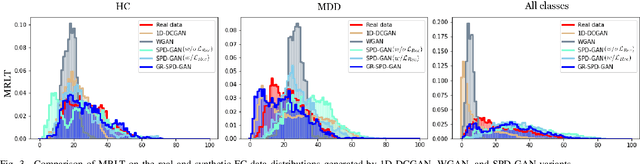
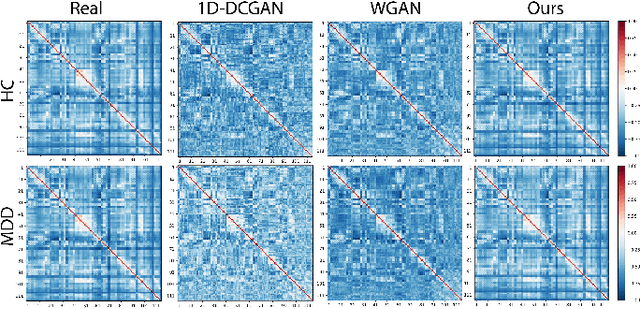
Common measures of brain functional connectivity (FC) including covariance and correlation matrices are semi-positive definite (SPD) matrices residing on a cone-shape Riemannian manifold. Despite its remarkable success for Euclidean-valued data generation, use of standard generative adversarial networks (GANs) to generate manifold-valued FC data neglects its inherent SPD structure and hence the inter-relatedness of edges in real FC. We propose a novel graph-regularized manifold-aware conditional Wasserstein GAN (GR-SPD-GAN) for FC data generation on the SPD manifold that can preserve the global FC structure. Specifically, we optimize a generalized Wasserstein distance between the real and generated SPD data under an adversarial training, conditioned on the class labels. The resulting generator can synthesize new SPD-valued FC matrices associated with different classes of brain networks, e.g., brain disorder or healthy control. Furthermore, we introduce additional population graph-based regularization terms on both the SPD manifold and its tangent space to encourage the generator to respect the inter-subject similarity of FC patterns in the real data. This also helps in avoiding mode collapse and produces more stable GAN training. Evaluated on resting-state functional magnetic resonance imaging (fMRI) data of major depressive disorder (MDD), qualitative and quantitative results show that the proposed GR-SPD-GAN clearly outperforms several state-of-the-art GANs in generating more realistic fMRI-based FC samples. When applied to FC data augmentation for MDD identification, classification models trained on augmented data generated by our approach achieved the largest margin of improvement in classification accuracy among the competing GANs over baselines without data augmentation.