Topological Cycle Graph Attention Network for Brain Functional Connectivity

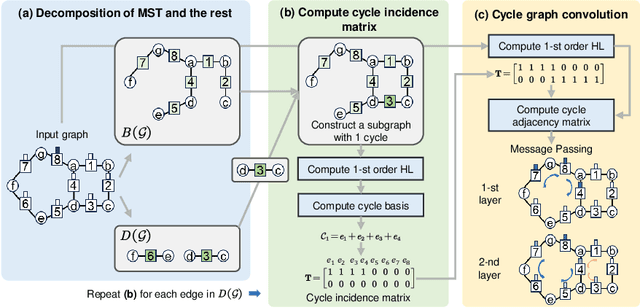
This study, we introduce a novel Topological Cycle Graph Attention Network (CycGAT), designed to delineate a functional backbone within brain functional graph--key pathways essential for signal transmissio--from non-essential, redundant connections that form cycles around this core structure. We first introduce a cycle incidence matrix that establishes an independent cycle basis within a graph, mapping its relationship with edges. We propose a cycle graph convolution that leverages a cycle adjacency matrix, derived from the cycle incidence matrix, to specifically filter edge signals in a domain of cycles. Additionally, we strengthen the representation power of the cycle graph convolution by adding an attention mechanism, which is further augmented by the introduction of edge positional encodings in cycles, to enhance the topological awareness of CycGAT. We demonstrate CycGAT's localization through simulation and its efficacy on an ABCD study's fMRI data (n=8765), comparing it with baseline models. CycGAT outperforms these models, identifying a functional backbone with significantly fewer cycles, crucial for understanding neural circuits related to general intelligence. Our code will be released once accepted.

Advancing Graph Neural Networks with HL-HGAT: A Hodge-Laplacian and Attention Mechanism Approach for Heterogeneous Graph-Structured Data

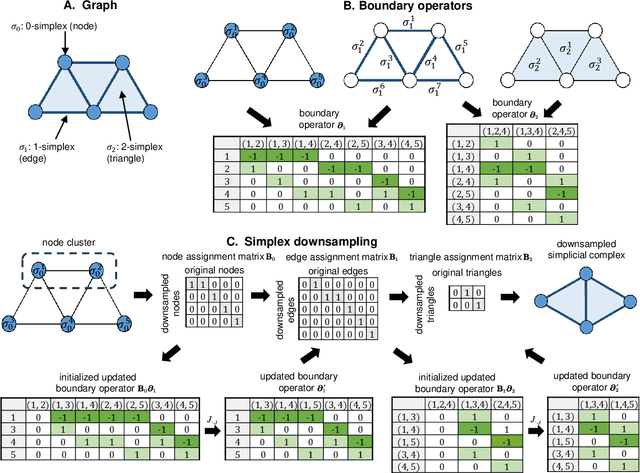
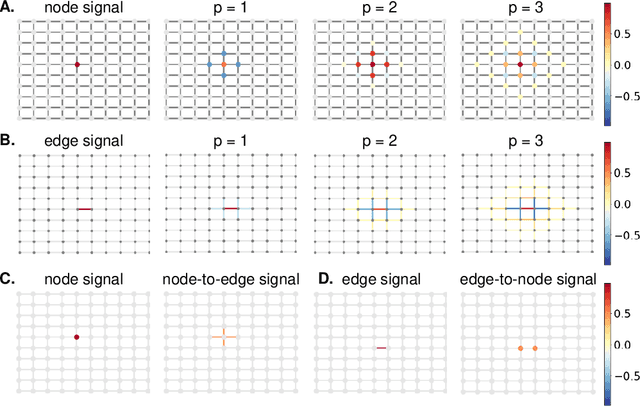
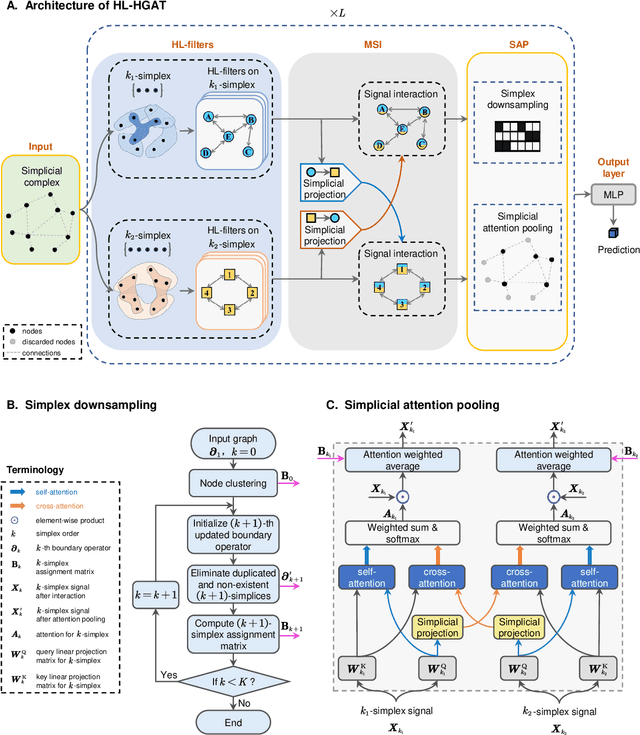
Graph neural networks (GNNs) have proven effective in capturing relationships among nodes in a graph. This study introduces a novel perspective by considering a graph as a simplicial complex, encompassing nodes, edges, triangles, and $k$-simplices, enabling the definition of graph-structured data on any $k$-simplices. Our contribution is the Hodge-Laplacian heterogeneous graph attention network (HL-HGAT), designed to learn heterogeneous signal representations across $k$-simplices. The HL-HGAT incorporates three key components: HL convolutional filters (HL-filters), simplicial projection (SP), and simplicial attention pooling (SAP) operators, applied to $k$-simplices. HL-filters leverage the unique topology of $k$-simplices encoded by the Hodge-Laplacian (HL) operator, operating within the spectral domain of the $k$-th HL operator. To address computation challenges, we introduce a polynomial approximation for HL-filters, exhibiting spatial localization properties. Additionally, we propose a pooling operator to coarsen $k$-simplices, combining features through simplicial attention mechanisms of self-attention and cross-attention via transformers and SP operators, capturing topological interconnections across multiple dimensions of simplices. The HL-HGAT is comprehensively evaluated across diverse graph applications, including NP-hard problems, graph multi-label and classification challenges, and graph regression tasks in logistics, computer vision, biology, chemistry, and neuroscience. The results demonstrate the model's efficacy and versatility in handling a wide range of graph-based scenarios.

Heterogeneous Graph Convolutional Neural Network via Hodge-Laplacian for Brain Functional Data

This study proposes a novel heterogeneous graph convolutional neural network (HGCNN) to handle complex brain fMRI data at regional and across-region levels. We introduce a generic formulation of spectral filters on heterogeneous graphs by introducing the $k-th$ Hodge-Laplacian (HL) operator. In particular, we propose Laguerre polynomial approximations of HL spectral filters and prove that their spatial localization on graphs is related to the polynomial order. Furthermore, based on the bijection property of boundary operators on simplex graphs, we introduce a generic topological graph pooling (TGPool) method that can be used at any dimensional simplices. This study designs HL-node, HL-edge, and HL-HGCNN neural networks to learn signal representation at a graph node, edge levels, and both, respectively. Our experiments employ fMRI from the Adolescent Brain Cognitive Development (ABCD; n=7693) to predict general intelligence. Our results demonstrate the advantage of the HL-edge network over the HL-node network when functional brain connectivity is considered as features. The HL-HGCNN outperforms the state-of-the-art graph neural networks (GNNs) approaches, such as GAT, BrainGNN, dGCN, BrainNetCNN, and Hypergraph NN. The functional connectivity features learned from the HL-HGCNN are meaningful in interpreting neural circuits related to general intelligence.