Unified Heat Kernel Regression for Diffusion, Kernel Smoothing and Wavelets on Manifolds and Its Application to Mandible Growth Modeling in CT Images

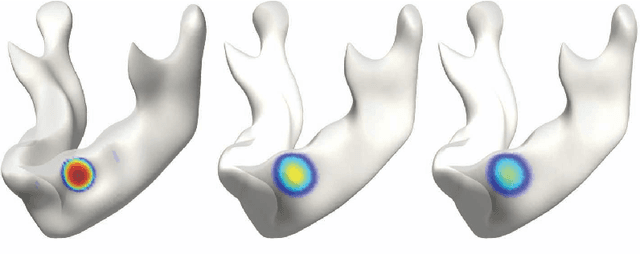
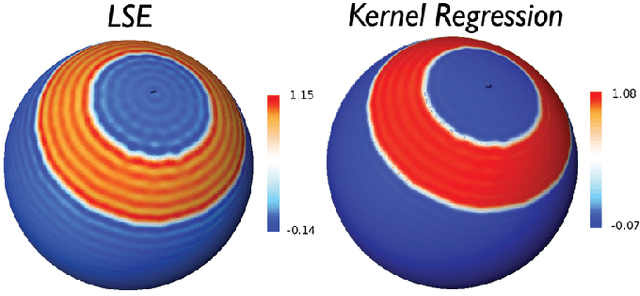
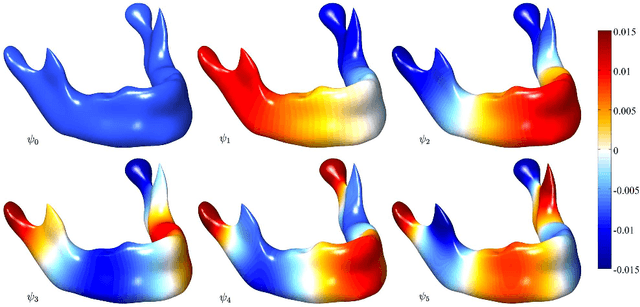
We present a novel kernel regression framework for smoothing scalar surface data using the Laplace-Beltrami eigenfunctions. Starting with the heat kernel constructed from the eigenfunctions, we formulate a new bivariate kernel regression framework as a weighted eigenfunction expansion with the heat kernel as the weights. The new kernel regression is mathematically equivalent to isotropic heat diffusion, kernel smoothing and recently popular diffusion wavelets. Unlike many previous partial differential equation based approaches involving diffusion, our approach represents the solution of diffusion analytically, reducing numerical inaccuracy and slow convergence. The numerical implementation is validated on a unit sphere using spherical harmonics. As an illustration, we have applied the method in characterizing the localized growth pattern of mandible surfaces obtained in CT images from subjects between ages 0 and 20 years by regressing the length of displacement vectors with respect to the template surface.