VolterraNet: A higher order convolutional network with group equivariance for homogeneous manifolds

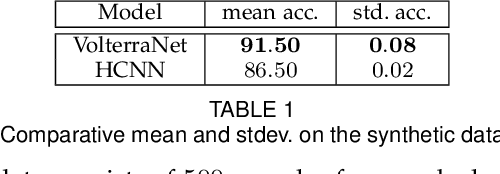
Convolutional neural networks have been highly successful in image-based learning tasks due to their translation equivariance property. Recent work has generalized the traditional convolutional layer of a convolutional neural network to non-Euclidean spaces and shown group equivariance of the generalized convolution operation. In this paper, we present a novel higher order Volterra convolutional neural network (VolterraNet) for data defined as samples of functions on Riemannian homogeneous spaces. Analagous to the result for traditional convolutions, we prove that the Volterra functional convolutions are equivariant to the action of the isometry group admitted by the Riemannian homogeneous spaces, and under some restrictions, any non-linear equivariant function can be expressed as our homogeneous space Volterra convolution, generalizing the non-linear shift equivariant characterization of Volterra expansions in Euclidean space. We also prove that second order functional convolution operations can be represented as cascaded convolutions which leads to an efficient implementation. Beyond this, we also propose a dilated VolterraNet model. These advances lead to large parameter reductions relative to baseline non-Euclidean CNNs. To demonstrate the efficacy of the VolterraNet performance, we present several real data experiments involving classification tasks on spherical-MNIST, atomic energy, Shrec17 data sets, and group testing on diffusion MRI data. Performance comparisons to the state-of-the-art are also presented.

A Statistical Recurrent Model on the Manifold of Symmetric Positive Definite Matrices

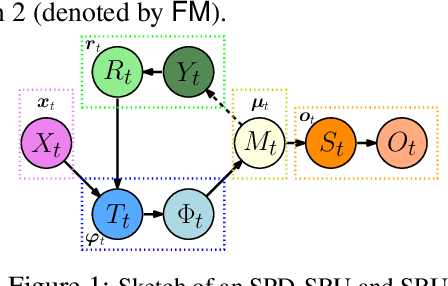
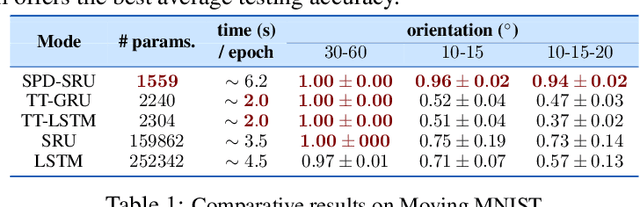
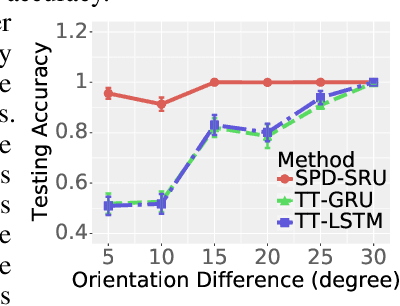
In a number of disciplines, the data (e.g., graphs, manifolds) to be analyzed are non-Euclidean in nature. Geometric deep learning corresponds to techniques that generalize deep neural network models to such non-Euclidean spaces. Several recent papers have shown how convolutional neural networks (CNNs) can be extended to learn with graph-based data. In this work, we study the setting where the data (or measurements) are ordered, longitudinal or temporal in nature and live on a Riemannian manifold -- this setting is common in a variety of problems in statistical machine learning, vision and medical imaging. We show how recurrent statistical recurrent network models can be defined in such spaces. We give an efficient algorithm and conduct a rigorous analysis of its statistical properties. We perform extensive numerical experiments demonstrating competitive performance with state of the art methods but with significantly less number of parameters. We also show applications to a statistical analysis task in brain imaging, a regime where deep neural network models have only been utilized in limited ways.

A CNN for homogneous Riemannian manifolds with applications to Neuroimaging

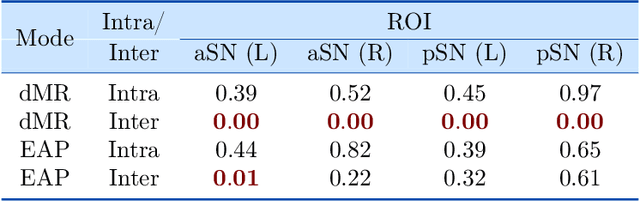
Convolutional neural networks are ubiquitous in Machine Learning applications for solving a variety of problems. They however can not be used in their native form when the domain of the data is commonly encountered manifolds such as the sphere, the special orthogonal group, the Grassmanian, the manifold of symmetric positive definite matrices and others. Most recently, generalization of CNNs to data domains such as the 2-sphere has been reported by some research groups, which is referred to as the spherical CNNs (SCNNs). The key property of SCNNs distinct from CNNs is that they exhibit the rotational equivariance property that allows for sharing learned weights within a layer. In this paper, we theoretically generalize the CNNs to Riemannian homogeneous manifolds, that include but are not limited to the aforementioned example manifolds. Our key contributions in this work are: (i) A theorem stating that linear group equivariance systems are fully characterized by correlation of functions on the domain manifold and vice-versa. This is fundamental to the characterization of all linear group equivariant systems and parallels the widely used result in linear system theory for vector spaces. (ii) As a corrolary, we prove the equivariance of the correlation operation to group actions admitted by the input domains which are Riemannian homogeneous manifolds. (iii) We present the first end-to-end deep network architecture for classification of diffusion magnetic resonance image (dMRI) scans acquired from a cohort of 44 Parkinson Disease patients and 50 control/normal subjects. (iv) A proof of concept experiment involving synthetic data generated on the manifold of symmetric positive definite matrices is presented to demonstrate the applicability of our network to other types of domains.

Dictionary Learning and Sparse Coding on Statistical Manifolds

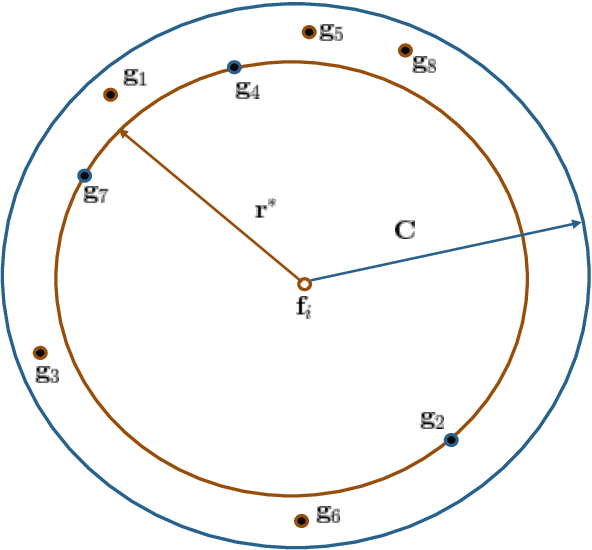
In this paper, we propose a novel information theoretic framework for dictionary learning (DL) and sparse coding (SC) on a statistical manifold (the manifold of probability distributions). Unlike the traditional DL and SC framework, our new formulation does not explicitly incorporate any sparsity inducing norm in the cost function being optimized but yet yields sparse codes. Our algorithm approximates the data points on the statistical manifold (which are probability distributions) by the weighted Kullback-Leibeler center/mean (KL-center) of the dictionary atoms. The KL-center is defined as the minimizer of the maximum KL-divergence between itself and members of the set whose center is being sought. Further, we prove that the weighted KL-center is a sparse combination of the dictionary atoms. This result also holds for the case when the KL-divergence is replaced by the well known Hellinger distance. From an applications perspective, we present an extension of the aforementioned framework to the manifold of symmetric positive definite matrices (which can be identified with the manifold of zero mean gaussian distributions), $\mathcal{P}_n$. We present experiments involving a variety of dictionary-based reconstruction and classification problems in Computer Vision. Performance of the proposed algorithm is demonstrated by comparing it to several state-of-the-art methods in terms of reconstruction and classification accuracy as well as sparsity of the chosen representation.

An information theoretic formulation of the Dictionary Learning and Sparse Coding Problems on Statistical Manifolds

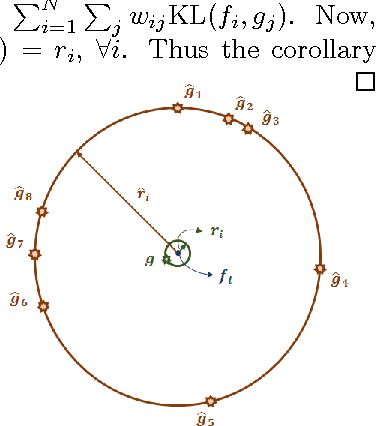
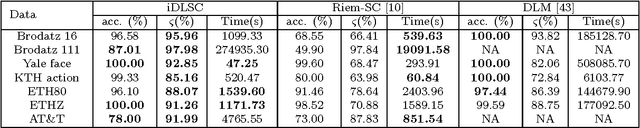
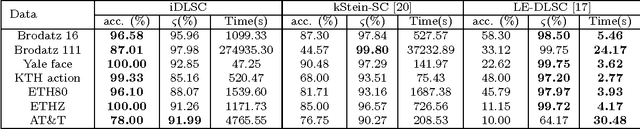
In this work, we propose a novel information theoretic framework for dictionary learning (DL) and sparse coding (SC) on a statistical manifold (the manifold of probability distributions). Unlike the traditional DL and SC framework, our new formulation {\it does not explicitly incorporate any sparsity inducing norm in the cost function but yet yields SCs}. Moreover, we extend this framework to the manifold of symmetric positive definite matrices, $\mathcal{P}_n$. Our algorithm approximates the data points, which are probability distributions, by the weighted Kullback-Leibeler center (KL-center) of the dictionary atoms. The KL-center is the minimizer of the maximum KL-divergence between the unknown center and members of the set whose center is being sought. Further, {\it we proved that this KL-center is a sparse combination of the dictionary atoms}. Since, the data reside on a statistical manifold, the data fidelity term can not be as simple as in the case of the vector-space data. We therefore employ the geodesic distance between the data and a sparse approximation of the data element. This cost function is minimized using an acceleterated gradient descent algorithm. An extensive set of experimental results show the effectiveness of our proposed framework. We present several experiments involving a variety of classification problems in Computer Vision applications. Further, we demonstrate the performance of our algorithm by comparing it to several state-of-the-art methods both in terms of classification accuracy and sparsity.